Постановка вопроса. Ставится задача разработать схему программного вычисления всех нулей функций многих переменных в области определения. Схему предполагается перенести на вычисление корней полиномов, а также нулей характеристического полинома матрицы коэффициентов системы линейных обыкновенных дифференциальных уравнений (ОДУ). Рассматриваемая схема используется для компьютерного анализа устойчивости системы ОДУ путем определения собственных значений матрицы коэффициентов системы ОДУ.
Схема сортировки и вычисление нулей функций нескольких переменных по индексам данных
Пусть вначале рассматривается функция одной переменной, для которой необходимо вычислить все минимумы
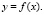(1)
В области определения функции задается промежуток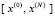 
. На промежутке 
, 
, 
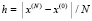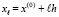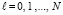считываются значения функции (1)
, 
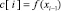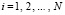. (2)
Значения c[i] функции f(x) сортируются. После осуществляется локализация минимумов функции в наперед заданной окрестности ε среди элементов (2), с помощью условного оператора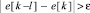 
, 
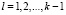. Где e[k] – индексы сортируемых элементов, располагающиеся на выходе по порядку отсортированного массива. Чтобы вычислить нули функции, необходимо на вход сортировки подать величины (2) взятые по модулю 
, 
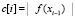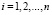, и искать нули как минимумы модуля.
Для нахождения минимумов для функции двух переменных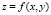 
внутри области определения 
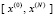и 
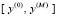задается прямоугольная сетка: 
, 
, 
, 
, 
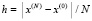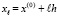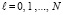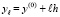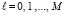. Далее осуществляется проход вдоль оси OY, j столбца прямоугольной сетки, в результате которого находится наименьшее значение 
, 
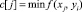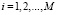, полученный минимум поступает на вход сортировки как j элемент одномерного массива. После чего оператор локализации минимума вычисляет все индексы минимумов функции двух переменных.
Описанная схема переносится для вычисления всех нулей функции z. На вход программы достаточно подать значения: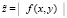 
. Нули функции локализуются как минимумы модуля [1–7, 17]. Таким образом, вычисляются все корни полиномов с комплексными коэффициентами [9, 10, 12, 13].
Локализация и вычисление собственных значений матриц
Собственные значения квадратной матрицы А размерности n×n определяются по описанной выше схеме как нули характеристического полинома:
.
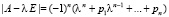Коэффициенты данного полинома вычисляются с помощью метода Леверье. Для этого необходимо решить систему уравнений Ньютона: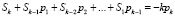 
. Здесь 
, 
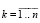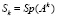– след матрицы Аk. Полином 
(
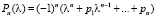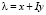) задается своими коэффициентами. Для того чтобы на вход метода подать соответственную полиному функцию f(x, y), применяется биномиальное разложение [3, 6, 8]; иначе значение полинома умножается на комплексно-сопряженное. В результате получим функцию 
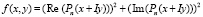. В случае если коэффициенты характеристического полинома вычислены с достаточной точностью, изложенный метод определения собственных значений матриц является устойчивым ввиду фактически верного вычисления нулей полиномов с учетом кратности [14–16].
Программное определение нулей характеристического полинома матрицы постоянных коэффициентов системы линейных ОДУ произвольного порядка
Пусть дана система линейных ОДУ в матричной форме с постоянными коэффициентами [8, 11, 22]
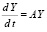, (3)
где Y и A – квадратные матрицы постоянных коэффициентов размерности n×n. Общее решение системы ОДУ (3) с постоянной матрицей A:
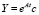. (4)
Начальные условия для (4):
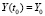, (5)
тогда решение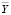 
удовлетворяет задаче Коши 
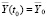. Ставится цель: провести исследование решения (4) системы ОДУ (3) на устойчивость в смысле Ляпунова [11, 12].
Рассмотрим подход к решению задачи анализа устойчивости, который основан на оценке устойчивости в соответствии с характеристическими нулями матрицы коэффициентов системы, то есть по виду собственных значений матрицы коэффициентов.
Из I теоремы Ляпунова об устойчивости известно, что нули характеристического полинома матрицы A из (3) имеют связь с характером устойчивости (3): в случае если все собственные значения имеют отрицательные действительные части, то система асимптотически устойчива; в противном случае система неустойчива [19, 20].
Отметим, что предложенный метод компьютерного анализа устойчивости содержит все аспекты анализа устойчивости по критериям Гурвица, Михайлова и Найквиста. Помимо этого, метод позволяет анализировать устойчивость и в случаях, не подпадающих под классические критерии (случай варьирования параметров системы ОДУ). Рассматриваемый метод применим для оценки устойчивости и асимптотической устойчивости во всех случаях без исключения. Классические критерии не всегда подходят для компьютеризации, а информацию об устойчивости, как правило, дают лишь косвенно, в виде, который характерен для качественной теории диффуравнений. К тому же метод основывается на алгоритме, который влечет однозначное указание на характер устойчивости, неустойчивости, асимптотической устойчивости в случае варьирования параметров решения систем линейных ОДУ с постоянными коэффициентами. Метод допускает использование в случаях, когда классические критерии невозможно применить, например при наличии трансцендентностей и нелинейностей в правой части.
Предложенный метод дает полную автоматизацию компьютерного анализа устойчивости. Отметим, что для определения знака действительной части нет необходимости точно вычислять нули полинома. Достаточно только произвести локализацию нулей, при этом сохраняется гарантия верных знаков их действительных частей. Таким образом произведена рационализация схемы компьютерного анализа устойчивости с точки зрения ее временной сложности.
Отметим, что в случае когда число нулей меньше степени многочлена, требуется локализовать действительные и мнимые части всех нулей с учетом их кратности.
Пример, приведенный ниже, показывает достаточность локализации действительных частей нулей характеристического полинома матрицы.
Пример 1. Пусть система (4) имеет матрицу коэффициентов:
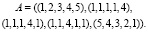
Необходимо определить знаки действительной части собственных значений матрицы. Ниже представлен алгоритм, который вычисляет действительные части собственных значений с точностью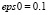 
.
Результаты вычислений: – 3.000; 2.510; – 0.430; 4.725; 9.985.
С помощью изложенной программы удается вычислить действительные части нулей с учетом знака за относительно малый период времен. Точность вычислений проигрывает по сравнению с результатами полной программы, однако это оказывается достаточным для того, чтобы сделать вывод о неустойчивости точки покоя системы. Предложенный метод используется для быстрого анализа устойчивости. В случае если действительные части положительны, то система неустойчива. Для достоверности оценки устойчивости можно осуществить локализацию действительных и мнимых частей нулей характеристического многочлена. Результат вычисления действительных и мнимых частей (полный код программы приводится в [6]):
|
Действительная часть нулей |
Мнимая часть нулей |
Значение функции |
|
– 3.00000000000000000E + 0000 2.51052877410466521E + 0000 – 4.28061588346591394E-0001 – 4.72255545982224341E + 0000 1.06400882740641695E + 0001 |
0.00000000000000000E + 0000 – 2.71473540786538243E-0029 – 6.52520446799852453E-0056 – 4.44724119213053305E-0029 – 4.38707603928584072E-0034 |
0.00000000000000E + 0000 1.23259516440783E-0032 5.49509021016461E-0106 3.25482160601443E-0032 2.30564629222262E-0029 |
С помощью изложенной схемы удается вычислить действительные и мнимые части нулей относительно точно. Вывод о состоянии равновесия точки покоя системы аналогичен предыдущему примеру.
Пример 2. Оценить устойчивость системы. Система имеет следующий вид:
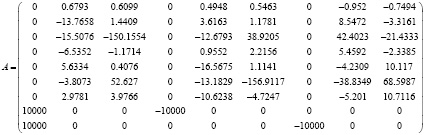
Листинг программы полностью приводится в [6]. Результат работы программы:
|
Действительная часть нулей |
Мнимая часть нулей |
Значение функции |
|
– 4.573 – 2.805 – 103.668 – 1.66.591 0.000 – 5.272 – 5.272 – 24.590 – 24.593 |
0.000 0.000 0.000 0.000 0.000 229.567 – 229.837 346.355 – 346.355 |
3.76070674693958763E + 0035 2.67668758647364437E + 0033 5.88014178051377293E + 0037 1.54394867607685689E + 0033 3.68630606796407673E + 0032 4.35465580557896453E + 0036 3.67676705867643764E + 0038 4.14596930357129645E + 0039 2.94264390362970963E + 0034 |
В списке нулей есть значение с нулевой действительной частью. Для того чтобы убедиться в том, что нуль не результат погрешности вычислений, корень возможно вычислить с помощью алгоритма поиска действительных нулей, так как мнимая часть является нулевой. Если действительная часть равна нулю, то система устойчива относительно состояния равновесия.
Заключение
Представлена схема программного вычисления нулей функций нескольких переменных в области определения функции. Данная схема применяется для вычисления корней полиномов с учетом кратности, а также для идентификации нулей характеристического полинома матрицы. Эта же модифицированная схема используется для компьютерного анализа устойчивости системы ОДУ на базе метода Леверье. За счет того, что изложенный алгоритм работает только с индексами данных входных элементов сортируемых последовательностей, исключено накопление погрешности, в результате чего достигается высокая точность вычислений. Чтобы определить характер устойчивости системы, необходимо просто идентифицировать нули характеристического полинома, и знак их действительной части, что ускоряет компьютерный анализ.