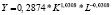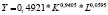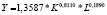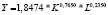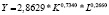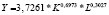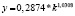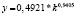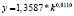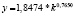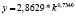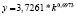К ключевым показателям регионов, из публикуемых в ежегодниках Росстата («Россия в цифрах») и представляющих большой научно-практический интерес, относятся ВРП, стоимость основных фондов и численность занятых. В зависимости от цели исследования возможны различные подходы к оценке экономических показателей, в том числе трех названных нами. Одним из подходов к оценке показателей на мезо- и макроуровнях является их оценка для совокупности экономических объектов в разные временные периоды. В настоящем исследовании оценка экономических показателей производится для совокупности всех регионов России за 2005, 2010, 2015 годы.
Оценить экономические показатели можно с разных позиций, разными методами, путем постановки различных задач, выбора разных совокупностей объектов (в нашем случае регионов) и т.д. Целью настоящего исследования является выявление и оценка зависимостей ВВП от стоимости основных фондов и численности занятых в экономике, а также зависимости производительности труда и фондовооруженности за каждый из трех временных периодов. Особенность двух зависимостей состоит в том, что в первом случае рассматривается зависимость между объемными показателями, а во втором случае – между относительными показателями. Напомним, что производительность труда – это объем продукции (в нашем случае ВРП), производимой в регионе в расчете на одного человека занятого в экономике, а фондовооруженность труда – стоимость основных фондов, приходящихся на одного человека, занятого в экономике.
Как известно, выявлять и оценивать связи и зависимости можно традиционными и/или новыми методами (новыми принято называть методы математического и компьютерного моделирования). Возможности традиционных методов анализа могут быть существенно расширены, если их перевести на компьютерную основу путем разработки так называемых моделей прямых расчетов [1]. Однако их возможности все же остаются весьма ограниченными.
Решение задач по выявлению и оценке связей, зависимостей и тенденций в экономике требует разработки и применения методов математического и компьютерного моделирования, возможности которых практически не ограничены. Однако и здесь существует весьма значительный ограничивающий фактор – низкий уровень знаний специалистов всех звеньев управления экономикой в сфере разработки и применения математических и компьютерных моделей в силу объективных и субъективных причин.
К объективным причинам можно отнести то, что система образования страны в период подготовки нынешнего поколения специалистов по экономике и управлению не предусматривала обучения методам моделирования. Ко второй из объективных причин следует отнести возросшие до огромнейших масштабов объемы информации. Субъективными причинами следует считать то, что поколение экономистов и управленцев, находящихся у руля управления отраслями экономики, высшим образованием и наукой страны, не создали эффективной системы повышения квалификации управленцев. Напомним в этой связи, что экономика 21 века называется информационной (знаниеориентированной и/или интернет-экономикой), предполагающей высокий уровень образования (как правило, высшее или среднее специальное образование), знаний и квалификации у всех работающих в системе управления в любой сфере человеческой деятельности. Чтобы управлять сложившейся и до неузнаваемости изменившейся экономикой, ее работникам на всех уровнях управления требуется владеть и применять в своей работе средства и инструменты, встроенные в различные прикладные программные продукты (в MS Office, в математические, статистические и другие пакеты прикладных программ), созданные и применяемые в развитых странах еще в прошлом веке.
Методы моделирования предусматривают изучение (исследование) социально-экономических процессов и явлений, систем и объектов экономики по их теоретическим образцам, называемым моделями. Моделирование позволяет в виде математических формул представить состояние экономики, ее объектов и различных сфер, варианты их развития, оценить и сопоставить результаты по разным вариантам, рассчитывать различные варианты прогнозов, проводить их сравнительную оценку и обоснованный выбор вариантов для реализации.
Разработка и анализ моделей для различных классов экономических задач привели к появлению научных дисциплин по их изучению, в первую очередь в системе высшего образования, таких как, Экономическая кибернетика; Математическая статистика; Математическая экономика и эконометрика; Методы принятия оптимальных решений; Специфические методы; Экспериментальные методы изучения экономики и др.
Дисциплина, изучающая методы и модели по выявлению и количественно-качественной оценке законов и закономерностей, связей и зависимостей, тенденций в экономике, а также методы и модели прогнозирования, получила название «Эконометрика» [3, 4, 5]. Зависимости между показателями в эконометрике оцениваются с помощью уравнений регрессии, которые в общем случае имеют вид y = f(x1,x2,…,xk), где y – зависимый экономический показатель, x1, x2, …, xk – показатели-факторы, от которых зависит Y.
В зависимости от количества показателей-факторов различают одно- и многофакторные уравнения регрессии. Особенность уравнений регрессии состоит в том, что они предназначены для выявления и оценки так называемых статистических зависимостей. Во-первых, эти зависимости являются зависимостями в среднем для совокупностей объектов; во-вторых, вид уравнения, с помощью которого можно описать исследуемую зависимость, заранее не известен.
В случае однофакторных зависимостей определенное представление о наличии и виде уравнения регрессии можно получить графическим методом, путем построения так называемых «графиков точек рассеивания» [1].
Первая из исследуемых зависимостей – ВРП (Y, млрд руб.) от стоимости основных фондов (К, млрд руб.) и численности занятых в экономике (L, тыс. чел.) – является двухфакторной, которую нельзя оценивать графически. Однако можно построить графики точек рассеивания для зависимости ВРП от каждого из двух факторов в отдельности и по виду этих графиков предположить наличие или отсутствие исследуемой зависимости. Такие графики, построенные нами, позволяют предположить наличие зависимости ВРП от каждого показателя-фактора в отдельности, а также от обоих показателей-факторов. В соответствии с этими графиками увеличение каждого из двух ресурсов (K, L) сопровождается ростом валового регионального продукта (Y). Зависимости за три рассматриваемых периода (2005, 2010 и 2015 гг.) кажутся весьма схожими, но имеют и существенные различия. Оценить эти различия только на основе графиков невозможно.
Вторая из рассматриваемых нами зависимостей является парной или однофакторной. Графики для однофакторных зависимостей позволяют судить о наличии и виде зависимости с большей степенью вероятности, чем в случае двух и более факторных зависимостей. Графики зависимости производительности труда от фондовооруженности, построенные по данным регионов за 2005, 2010 и 2015 гг., подтверждают этот вывод.
Построение графиков и их анализ показали, что два региона, г. Москва и Тюменская область, резко выделяются среди всех остальных величинами рассматриваемых показателей (эти два региона являются самыми экономически благополучными). Величины показателей этих двух регионов оказывают большое влияние на вид, степень, параметры и характеристики рассматриваемых зависимостей. Поэтому оценка зависимостей проведена нами в двух вариантах: для совокупности всех регионов и для регионов без г. Москвы и Тюменской области.
Проведенный нами анализ графиков не позволяет однозначно судить о виде рассматриваемых зависимостей. Однако графики позволяют предположить, что зависимость является линейной или нелинейной, но весьма близкой к линейной. В соответствии с математикой такими нелинейными уравнениями являются, в частности, уравнения показательного и степенного видов. Поэтому для каждой зависимости за каждый год нами построены по три уравнения: линейного, показательного и степенного видов.
Построить уравнение регрессии означает рассчитать их параметры и статистические характеристики. Вторая группа показателей (статистические характеристики) предназначены для оценки приемлемости построенного уравнения регрессии. Количество таких характеристик составляет более десятка. Проведенные нами расчеты и их анализ показывает, что в каждом конкретном случае нет необходимости оценивать весь перечень статистических характеристик [1].
Часть статистических характеристик, необходимых для оценки связей и зависимостей, можно рассчитать на ПЭВМ с помощью встроенных функций MS Excel. Наряду со статистическими характеристиками из MS Excel нами рассчитана и анализируется еще одна очень важная, с нашей точки зрения, статистическая характеристика, называемая средней ошибкой аппроксимации (A), которую можно определить по формуле
,
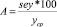где sey – стандартная ошибка для оценки y, yср – средняя арифметическая величина зависимого показателя Y.
В соответствии с величинами индекса детерминации (r2) все три вида уравнений регрессии за все три периода для двухфакторной зависимости ВРП от стоимости основных фондов и численности занятых в экономике являются приемлемыми. При этом уравнения линейного и степенного видов равноприемлемы (индекс превышает 0,93). Степень зависимости при такой величине r2 считается очень высокой. Индекс r2 для зависимости показательного вида находится в пределах 0,7 (степень зависимости при такой величине r2 считается выше средней).
Более определенное представление о приемлемости рассматриваемых трех видов двухфакторных уравнений можно получить по величине средней ошибки аппроксимации (A). В учебной литературе по эконометрике считается, что если величина A < 10 %, то построенный вид уравнения является «хорошим».
В нашем случае по данным за все три периода «хорошими» оказались уравнения степенного вида, для которых величина составила 5,0; 4,1 и 3,2 % соответственно за 2005, 2010 и 2015 гг. Для зависимостей показательного вида величина (A) находится в пределах 29,1–22,3 (по годам она уменьшилась). При таких значениях средняя ошибка аппроксимации зависимости может, с нашей точки зрения, считаться приемлемой на удовлетворительном уровне. Зависимости линейного вида по величинам ошибки аппроксимации оказались неприемлемыми.
Приемлемость уравнений регрессии, выражающих зависимость производительности труда (y) от фондовооруженности (k), можно оценить следующим образом:
– по величине r2 за все три периода предпочтительны уравнения регрессии линейного вида, а по величине средней ошибки аппроксимации (A) – уравнения степенного вида;
– приемлемыми на хорошем уровне (A < 10 %) можно считать уравнения показательного вида, а на удовлетворительном уровне – уравнения линейного вида (A < 25 %);
– по всем трем видам уравнений степень тесноты связи (следовательно, приемлемость уравнений регрессии) в 2010 и 2015 годы возросла.
Основными показателями, для изучения которых строятся уравнения регрессии, выражающие связи и зависимости, являются параметры этих уравнений. Однако их анализ проводится только после обоснования приемлемости выбранных видов уравнений. В соответствии с нашими расчетами приемлемыми являются в нашем случае двухфакторные уравнения производственных функций показательного и степенного видов и все три однофакторных уравнения для зависимости производительности труда от фондовооруженности [1, 2].
Задача выявления связей и зависимостей не ограничивается построением их уравнений. Ценность уравнений регрессии состоит и в том, что с их помощью можно рассчитать и оценить ряд показателей: предельный эффект и коэффициент эластичности для каждого показателя-фактора; изокванты; предельные нормы взаимозаменяемости показателей-факторов; изоклинали и др. При этом для однофакторных уравнений можно рассчитать только первый и второй из показателей, а для двух- и более факторных – все перечисленные [1, 3].
Предельный эффект и коэффициент эластичности рассчитываются по формулам
; 
.
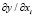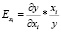Оба показателя имеют экономическую интерпретацию: предельный эффект представляет собой величину, на которую увеличится зависимый показатель (y) при увеличении показателя-фактора (х) на одну единицу; коэффициент эластичности – величина в процентах, на которую увеличится зависимый показатель при увеличении показателя-фактора на 1 %.
С точки зрения возможности экономического истолкования параметров более предпочтительными и ценными являются уравнения, выражающие зависимости линейного и степенного типов.
Для уравнений линейного вида ∂y/∂xi = mi, где mi – параметр (коэффициент) при показателе-факторе xi. Для нелинейных уравнений предельный эффект является переменной величиной, которая выражается формулой. Для уравнений степенного вида коэффициент эластичности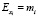 
, где mi – параметр (показатель степени) для показателя-фактора xi. Для остальных видов уравнений коэффициент эластичности является переменной величиной.
Напомним, что нами построены два варианта уравнений регрессии: для всей совокупности регионов и для совокупности регионов без г. Москвы и Тюменской области.
По параметрам и статистическим характеристикам, рассчитанным нами для обоих вариантов уравнений регрессии, можно сформулировать ряд выводов, наиболее значимыми из которых являются следующие:
– по величинам индекса детерминации (r2) и средней ошибки аппроксимации (А) все три вида уравнений регрессии для зависимости Y от k за все три периода можно считать приемлемыми; при этом зависимость степенного вида является заслуживающей оценки «хорошо» (А < 10 %), на втором месте по приемлемости оказалась зависимость линейного вида;
– соотношение величин параметров уравнений регрессии m1 и m2 по годам менялось в пользу m2, т.е. m1 уменьшался, а m2 увеличивался; коэффициенты m1, m2 в случае линейной зависимости представляют собой предельные эффекты, а в случае степенной зависимости – коэффициенты эластичности; следовательно, можно утверждать, что показатели эффективности использования основных фондов снизились, а эффективности использования численности занятости в экономике выросли;
– по величинам индекса детерминации зависимости производительности труда от фондовооруженности можно назвать средними по приемлемости (по годам они заметно выросли); по величинам (А) зависимости степенного и показательного видов оказались даже заслуживающими оценки «хорошо», т.е. А < 10 %; линейную зависимость также можно считать приемлемой, но с удовлетворительной оценкой.
Сравнение статистических характеристик для совокупности всех регионов и для совокупности регионов без г. Москвы и Тюменской области показывает, что по величинам r2 первая совокупность имеет незначительное предпочтение по степени тесноты зависимости, но по величинам средней ошибки аппроксимации почти по всем уравнениям за все три временных периода приемлемость совокупности регионов без г. Москвы и Тюменской области заметно выше. Рассмотрение двух совокупностей регионов преследует цель показать различие в величинах параметров и степени влияния на эти параметры двух самых крупных и благополучных регионов.
Математическая запись двухфакторных степенных уравнений производственных функций и однофакторных степенных уравнений для зависимости производительности труда от фондовооруженности, построенных по данным регионов России за 2005, 2010 и 2015 гг.
|
Для всей совокупности регионов |
Индекс детерм. |
Для совокупности регионов без г. Москвы и Тюменской области |
Индекс детерм. |
|
|
Двухфакторные уравнения производственных функций |
||||
|
2005 |
|
0,6585 |
|
0,5679 |
|
2010 |
|
0,6715 |
|
0,5768 |
|
2015 |
|
0,7367 |
|
0,6696 |
|
Уравнения зависимости производительности труда от фондовооруженности |
||||
|
2005 |
|
0,6585 |
|
0,5679 |
|
2010 |
|
0,6715 |
|
0,5768 |
|
2015 |
|
0,7367 |
|
0,6696 |
Важнейшими показателями, которые могут быть рассчитаны и оценены для многофакторных уравнений регрессии, являются изокванты и предельные нормы взаимозаменяемости показателей-факторов [4–6]. Особенно ценны эти показатели, если уравнения регрессии представляют собой формулы производственных функций. В нашем случае уравнения зависимостей ВРП (Y) от стоимости основных фондов (K) и численности занятых в экономике (L) являются производственными функциями [3].
Изоквантой (для уравнения регрессии) называют формулу, с помощью которой можно определить численные значения показателей-факторов, при которых величина зависимого показателя принимает одно и то же заранее заданное значение, т.е. y = const.
Для линейного уравнения производственной функции Y = b + m1K + m2L изокванту можно записать в виде одной из следующих формул: K = (Y – b – m2*L)/ m1 или L = (Y – b – m1*k)/m2, где У = const. В принципе это не две разные, а одна и та же изокванта, записанная по-разному.
Линейное уравнение для зависимости Y от K, L, построенное нами для второй совокупности регионов России за 2015 г., имеет вид
Y = – 81,323 + 0,2697*K + 0,3480*L.
Если Y (ВРП) принять равным его среднему арифметическому значению, т.е. Y = const = 521,9 млрд руб., то для этого уравнения формула изокванты будет иметь вид
K = (Y + 81,323 + 0,3480*L)/ 0,2697.
Откуда
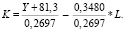
Подставляя Y = const = 521,9, получим K = 2236,6 – 1,2903*L.
Если в полученные уравнения изокванты вместо показателя L (численность занятых в экономике) подставлять какие-либо из возможных для него числовых значений, то можно найти соответствующие значения для показателя K (стоимости основных фондов). При любых значениях пары показателей–факторов K, L зависимый показатель Y (ВРП) будет принимать одно и то же значение Y = 521,9 млрд руб.
Изокванта представляет самостоятельный аналитический интерес, но имеет еще одно важное назначение: с ее помощью можно рассчитывать предельные нормы взаимозаменяемости показателей-факторов, которые представляют собой формулы производной одного фактора по другому, определяемые по формулам изоквант.
Для линейного уравнения производственной функции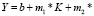 
L предельные нормы взаимозаменяемости показателя-фактора K определяются по формуле
,
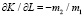а для уравнения степенного вида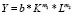 
– по формуле
.
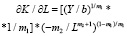Особый интерес среди уравнений производственных функций представляет производственная функция степенного вида, получившая название функции Кобба – Дугласа: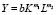 
[1, 5, 6]. Этот интерес обусловлен несколькими обстоятельствами: во-первых, параметры m1 и m2 имеют экономический смысл (показывают рост зависимого показателя Y в процентах при увеличении каждого из показателей-ресурсов на 1 процент); во-вторых, экономический смысл имеет и суммарная величина (m1 + m2) (если увеличить величины ресурсов K и L на 1 % каждый, то Y увеличится на (m1 + m2) %); в-третьих, модель 
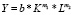можно преобразовать в другой вид, представляющий не меньший интерес; если m1 + m2 = 1 (откуда m2 = 1 – m1), то вышерассмотренное уравнение производственной функции можно записать в виде 
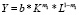или в виде 
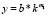, выражающего зависимость производительности труда (Y) от его фондовооруженности (k).
В таблице приведена математическая запись полученных нами уравнений степенного вида для всей совокупности регионов и для совокупности регионов без г. Москвы и Тюменской области.
По таблице можно сформулировать ряд выводов, в частности следующие: во-первых, в соответствии с величинами индексов детерминации (r2) степень тесноты зависимости ВРП от стоимости основных фондов и численности занятых в экономике за рассматриваемые временные периоды для обеих совокупностей регионов усилилась; во-вторых, в соответствии с величинами коэффициентов эластичности (Ek = m1; EL = m2) эластичность основных фондов снижалась, а эластичность численности в экономике – росла (для обеих совокупностей регионов); в-третьих, эластичность показателя фондовооруженности в уравнениях для зависимости производительности труда по обеим совокупностям снижается; в-четвертых, для совокупности всех регионов эластичность основных фондов выше, а эластичность численности занятых в экономике ниже, чем для совокупности регионов без г. Москвы и Тюменской области; в-пятых, эластичность фондовооруженности для совокупности всех регионов выше, чем для совокупности регионов без г. Москвы и Тюменской области.