Одной из важнейших задач в системах учета сырья деревообрабатывающей промышленности является измерение геометрических характеристик лесо- и пиломатериалов. Особенно актуальна эта задача для определения количества и объема круглых лесоматериалов, уложенных в штабели, поскольку применяемые в настоящее время ручные методы измерения дают погрешность более 15 % [8]. Решение этой проблемы возможно благодаря использованию измерительной системы на основе технического зрения, когда положение, форма и размеры бревен определяются специализированным программным обеспечением по их фотоизображениям. Выбор указанного подхода влечет за собой необходимость решения типичной для систем машинного зрения задачи – распознавания образов. Сложность такой задачи состоит в том, что предварительно необходимо обнаружить каждый срез бревна на изображении.
Обзор существующих решений
Распознаванию срезов бревен на изображениях было посвящено несколько работ [5, 6, 8–10], некоторые из них нашли практическое применение в составе прикладных измерительных систем [8–10]. Предложенные в данных работах методы детектирования можно разделить на две категории. К первой группе относятся методы, основанные на машинном обучении. В [6] авторы предложили итеративную схему детектирования и сегментации, в которой на этапе обнаружения срезов бревен используются дескрипторы особых точек на основе гистограммы направленных градиентов (англ. HOG – histogram of oriented gradients) [2] совместно с признаками Хаара и операторами локальных двоичных шаблонов (англ. LBP – local binary patterns) [13]. В работе [5] для поиска бревен по их ключевым признакам используется метод Виолы - Джонса [14]. Основная его идея заключается в использовании каскада классификаторов, каждый из которых является комитетом (ансамблем) слабых классификаторов. В качестве признаков для алгоритма распознавания используются прямоугольные признаки Хаара.
Методы второй группы построены по схеме обучения без учителя и используют предположения об известной форме и размерах бревен [4, 9, 10]. В основном эти методы основаны на преобразовании Хафа или его модификациях и применяются для обнаружения срезов бревен на изображении в виде окружностей или эллипсов. К недостаткам таких методов следует отнести невысокую степень автоматизации процесса детектирования, что влияет в конечном счете на объективность результатов измерения. Причинами тому являются хорошо известные недостатки преобразования Хафа:
- чувствительность к геометрическим искажениям объектов и шумам;
- отсутствие априорной информации о размерах объектов на изображении;
- как следствие, вычислительная сложность алгоритма.
Такие ограничения, на наш взгляд, не позволяют в полной мере использовать данные методы и получать высокое качество детектирования для задачи распознавания бревен. Тем не менее авторам одной из таких работ удалось достичь величины средней вероятности обнаружения 95,7 % [10].
В условиях данной задачи наиболее перспективными и предпочтительными с точки зрения вычислительной трудоемкости и требованиям к искажениям объектов являются методы, основанные на машинном обучении. Для поиска срезов бревен на изображениях предлагается использовать подход, предложенный в [2], но с некоторыми изменениями. В указанной работе реализован классический HOG-детектор, использующий в качестве классификатора метод опорных векторов (англ. SVM – support vector machine). Авторами данной работы рассмотрена реализация HOG-детектора с использованием ансамбля решающих деревьев [1] и исследуется зависимость его работы от входных параметров.
Материалы и методы исследования
Гистограммы направленных градиентов – это метод признакового описания, характеризующего форму объекта. Изначально данный метод был применен для задач обнаружения людей на изображениях, однако последующие исследования показали его эффективность для множества других задач классификации [3, 11].
Реализация признакового описания бревен в данной работе построена по общей схеме описания HOG-дескриптора на основе подсчета количества направлений градиента в ячейках изображения, как изложено в статье [2]. На рис. 1 приведена схема такого разбиения на ячейки и вычисления гистограммы градиентов для задачи детектирования бревен.
Анализ набора из более чем 7000 изображений пачек бревен [7] показал, что характерные особенности изображений подвержены многим факторам, таким как освещение, деформация формы, частичное перекрытие срезов стволов, различный ракурс съемки и масштаб снимков, и требуют применения специальных методов для быстрого вычисления признаков бревен. Чтобы преодолеть указанные ограничения исходных данных, в работе используются следующие решения:
1. Для быстрого вычисления HOG-дескрипторов градиенты входных изображений предварительно были представлены в интегральном виде. Данная техника основана на дискретной теореме Грина и позволяет быстро вычислять гистограммы направленных градиентов в интересующей области (ячейках) изображения за несколько простейших арифметических операций [15], при этом время вычисления не зависит от площади ячеек снимка.
2. Для обеспечения инвариантности к масштабу, HOG-дескрипторы вычисляются в скользящем окне с минимальным шагом на нескольких масштабах исходного изображения. Данное решение позволяет осуществить поиск изображений срезов бревен в широком диапазоне их размеров (радиусов).
3. Неравномерность освещения бревен частично компенсируется за счет повышения контрастности исходного изображения [2].
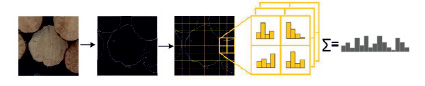
а) б) в) г) д)
Рис. 1. Схема вычисления HOG-дескрипторов: а) входное изображение; б) градиент входного изображения; в) разбиение изображения на ячейки; г) объединение ячеек в блоки и нормализация векторов признаков; д) объединение нормированных гистограмм блоков в один дескриптор
В качестве классификатора в работе используется алгоритм обучения случайных решающих деревьев (англ. Random Forest) [1]. Основная его идея заключается в построении ансамбля деревьев принятия решений, при этом классификация – отнесение нового объекта к тому или иному классу производится путём голосования: каждое дерево относит классифицируемый объект к одному из классов, и «побеждает» тот класс, за который проголосовало наибольшее количество деревьев. К достоинствам данного метода относится:
- высокая точность классификации;
- высокая масштабируемость и параллелизуемость;
- способность эффективно обрабатывать данные с большим числом признаков и классов;
- способность оценки важности отдельных признаков.
Существуют и недостатки, такие как:
- алгоритм склонен к переобучению, особенно на зашумленных данных;
- большой размер получающихся моделей.
Для оценивания обобщающей способности классификатора используется k-блочная кросс-проверка [12], когда вся выборка данных случайным образом разбивается на k непересекающихся блоков одинакового размера. Каждый блок по очереди становится тестовой выборкой, при этом обучение производится по остальным k-1 блокам. Результатом такого тестирования является средняя ошибка на контрольной выборке данных. Данный метод дает несмещенную оценку вероятности ошибки, а значит, позволяет обнаружить переобучение классификатора.
Результаты исследования и их обсуждение
Для оценки предложенных решений был проведен ряд экспериментов, призванных оценить качество классификации на реальных данных при различных параметрах построения HOG-дескриптора и классификатора. В качестве тестовых данных использовались 11068 размеченных изображений с 4632 «положительными» снимками бревен и 6436 изображений с «отрицательными» образцами. Примеры изображений обучающей выборки приведены на рис. 2.
 а)
а)  б)
б)
Рис. 2. Примеры изображений из обучающей выборки: а) «положительные» примеры; б) «отрицательные» примеры
 а)
а) 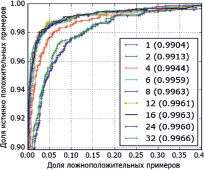 б)
б)
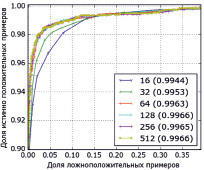
Рис. 3. Сравнение качества работы ансамбля решающих деревьев: а) изменение количества деревьев; б) ограничение глубины дерева
 а)
а)  б)
б)
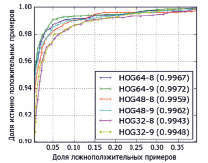
Рис. 4. Сравнение качества работы HOG-детекторов на основе ансамбля решающих деревьев: а) кривая рабочей характеристики; б) кривая компромиссного определения ошибки



Рис. 5. Детектирование срезов бревен
Подбор параметров HOG-дескриптора
|
Параметры HOG-дескриптора [2] |
Результаты экспериментов |
|||||
|
Имя |
Размер окна/ блока/ ячейки, пикс. |
Количество ячеек гистограммы |
Шаг блока, пикс. |
Полнота, % |
Точность, % |
F-метрика, % |
|
HOG64-8 |
64/16/8 |
8 |
8 |
95,0 ± 0,8 |
99,0 ± 0,1 |
96,9 ± 0,5 |
|
HOG64-9 |
64/16/8 |
9 |
8 |
95,4 ± 0,5 |
99,1 ± 0,3 |
97,1 ± 0,3 |
|
HOG48-8 |
48/12/6 |
8 |
6 |
94,5 ± 0,6 |
98,5 ± 0,4 |
96,6 ± 0,2 |
|
HOG48-9 |
48/12/6 |
9 |
6 |
95,0 ± 0,8 |
98,7 ± 0,3 |
96,9 ± 0,4 |
|
HOG32-8 |
32/8/4 |
8 |
4 |
94,2 ± 0,8 |
97,8 ± 0,4 |
95,7 ± 0,6 |
|
HOG32-9 |
32/8/4 |
9 |
4 |
94,1 ± 0,9 |
97,6 ± 0,1 |
95,7 ± 0,5 |
В первом эксперименте исследовались зависимости эффективности предсказательной способности ансамбля решающих деревьев от входных параметров этого классификатора. На рис. 3 приведено сравнение моделей, обученных с использованием различного количества случайных решающих деревьев (рис. 3, а) и различной глубины построения каждого дерева (рис. 3, б).
Анализ кривых рабочей характеристики (англ. ROC – receiver operating characteristic) показывает, что с увеличением количества деревьев с 16 до 64 качество распознавания значительно улучшается (площадь под кривыми увеличивается). При дальнейшем увеличении количества деревьев с 128 до 512 рост качества практически прекращается. Таким образом, можно предположить, что оптимальное количество деревьев для задачи распознавания бревен лежит в диапазоне между 64 и 128 (рис. 3, а). На основе аналогичных выводов можно показать, что необходимая глубина построения дерева лежит в диапазоне между 6 и 8 (рис. 3, б). По этим причинам в дальнейших исследованиях нами использовались классификаторы, состоящие только из 64 деревьев с максимальной глубиной построения 6.
В рамках второго эксперимента были исследованы результаты работы классификаторов, обученных на шести различных наборах признаков. Параметры исследуемых HOG-дескрипторов и соответствующие им характеристики детекторов приведены в таблице. Для того чтобы понять, как и в каких пределах изменяются рабочие характеристики классификаторов в зависимости от параметров HOG-дескрипторов, приведены поясняющие рисунки. Визуализация качества работы классификаторов представлена двумя графиками: кривыми рабочей характеристики (рис. 4, а) и кривыми компромиссного определения ошибки (англ. DET – detection error trade-off) (рис. 4, б). Полученные графики достаточно наглядно характеризуют предсказательную способность построенных моделей. Видно, что наиболее близко к левому нижнему углу системы координат расположена кривая, соответствующая дескриптору с 9 ячейками гистограммы и размером окна 64 пикселя (рис. 4, б).
Этому же дескриптору соответствует кривая с максимальной площадью 0,9972 (рис. 4, а). Это означает, что классификатор с таким дескриптором обладает наилучшей предсказательной способностью. Данные выводы подтверждаются рассчитанными характеристиками: дескриптор с именем HOG64-9 имеет максимальные значения из представленных величин полноты и точности классификаторов (таблица).
Таким образом, из результатов экспериментов можно заключить, что набор признаков HOG64-9 является лучшим среди рассмотренных. Такой классификатор способен обнаруживать положительные примеры (бревна) с вероятностью 95,4 % при уровне ложного срабатывания 10-3 (рис. 4, б). Иллюстрация работы алгоритма детектирования приведена на рис. 5.
Заключение
Результаты экспериментов показали, что предложенный HOG-детектор на основе обучения случайных решающих деревьев достигает более высоких показателей качества по сравнению с методами, основанными на линейных классификаторах (SVM + HOG, точность 77,9 % [6]) и каскадах слабых классификаторов (AdaBoost+Haar, точность 95,1 % при величине ложных срабатываний 4,9•10-3). Однако он уступает данным методам при усилении последних несколькими комбинированными признаками и использовании информации о текстуре и цвете бревен (LBP + HOG + GMM, точность 99,3 % при величине ложных срабатываний 3,6•10-3[6]).
Дальнейшим направлением исследований, представленных в работе, является построение эффективных алгоритмов контурного анализа и пиксельной сегментации и исследование этих методов для задачи точного измерения срезов бревен по их фотоизображениям.



