Успешное функционирование наземных комплексов космического назначения (НККН) в значительной степени зависит от бесперебойной работы специальных технических систем, важнейшей из которых является система гарантированного электропитания (СГЭП).
СГЭП предназначена для бесперебойного и гарантированного обеспечения всех потребителей НККН электрической энергией в соответствии с государственными стандартами [1], определяющими требования к качеству электроэнергии в режимах дежурства, штатной работы, а также при аварийных отключениях от основных источников.
При разработке математического обеспечения распознавания отказов в технических системах важнейшими задачами являются формирование множества контролируемых признаков и формальное описание на данной основе каждого отказа.
В дальнейшем формальное описание отказа ДГУ СГЭП, как составной части математической модели, называется его изображением. Изначально приведенное множество контролируемых показателей в ДВС РИЭ, как правило, является избыточным. Необходимо определить минимальное множество таких показателей, что позволит снизить размерность математической модели, при этом повышая ее достоверность, а следовательно, и надежность ДГУ СГЭП. Это обусловлено снижением количества измерений в системах, каждое из которых сопровождается методическими и метрологическими погрешностями, а также и уменьшением времени на принятие решений по устранению выявленных отказов.
В настоящей статье рассматривается метод формального описания отказов по основным рабочим диагностическим признакам ДГУ СГЭП, в котором, в отличие от известных методов, совмещены процессы построения отображений отказов и выбора минимального множества контролируемых диагностических признаков.
В работе [2] предложен подход к преобразованию траекторий выходных процессов системы на основе теории пространств измеримых функций и интеграла Лебега. В результате преобразования траекторий формируется вектор Y<n’> числовых характеристик, которые и принимаются в качестве диагностических признаков ДГУ СГЭП. Этот вектор называется наблюдаемым состоянием исследуемой системы (в дальнейшем – «системы») [7].
Теоретико-множественная формулировка задачи построения изображений отказов ДГУ
На множестве векторов Y<n’> может быть задана структура n'-мерного евклидова пространства Y. В данном пространстве выделяются подмножества Yi (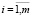
) наблюдаемых состояний системы, каждое из которых соответствует недопустимым значениям (отказу) по i-му диагностическому признаку ДГУ СГЭП. Подмножества Yi с топологической точки зрения представляют собой области в пространстве Y.
В общем случае области Yi частично пересекаются между собой. Иначе, элементы Y<n’> находятся между собой в отношении толерантности Ω⊂Y×Y, которое обладает следующими свойствами [3]: рефлексивности: ∀Y∈Y, (Y, Y)∈Ω; симметричности: ∀Y1, Y2∈Y: (Y1, Y2)∈Ω⇒(Y2, Y1)∉Ω; антитранзитивности: ∃Y1, Y2, Y3∈Y: (Y1, Y2)∈Ω, (Y2, Y3)∈Ω⇒(Y1, Y3)∉Ω. Из приведенных свойств вытекает, что области Yi (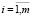
) могут рассматриваться как классы толерантности, а фактор-пространство Y/Ω = = {Yi|
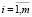} является покрытием пространства Y [7].
Процесс отнесения текущего состояния системы к той или иной области Yi в покрытии Y/Ω характеризуется значительной степенью неопределенности из-за наличия пересечений областей и может давать ошибочные результаты. Поэтому очевидно, что при разработке математической модели распознавания отказов системы каждую область Yi необходимо заменить одним элементом – изображением i-го отказа
, 
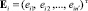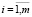, (1)
которое интегрально описывает свойства всей области.
Известно, что на евклидовых пространствах реализуется принцип сжимающих отображений [3, 4]. В соответствии с данным принципом всегда может быть найдена та или иная вычислительная схема, которая позволяет выразить целую область изображением вида (1). Такие вычислительные схемы имеют единую математическую основу и реализуются в рамках процедур обучения.
Теоретические основы обучающей процедуры
Пусть задан перечень всех отказов по диагностическим признакам ДГУ СГЭП
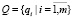; (2)
– определён состав контролируемых показателей ДГУ СГЭП
Y = (y1, y2,…, y n′)т; (3)
– сформирована ограниченная по объёму обучающая выборка реализаций наблюдаемых состояний (образов), соответствие которых каждому отказу известно:
,
,…,
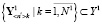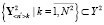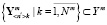, (4)
где Ni – мощность множества обучающих образов, содержащихся в области Yi.
На основе исходных данных (2)–(4) требуется построить изображения (1), которые оптимальным образом (в смысле достоверности распознавания) описывают признаки соответствующих отказов qi (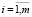
).
Обучающая выборка (4), как правило, является неоднородной и ограниченной по объёму. Следовательно, для обучения необходимо использовать методы непараметрической статистики [6], которые позволяют обрабатывать неоднородную статистическую информацию малого объёма. Одним из них является метод стохастической аппроксимации, который базируется на операциях итеративного градиентного поиска. В соответствии с данным методом для каждого подмножества Yi ищется аппроксимация разделяющей функции hi в n′-мерном евклидовом пространстве Y, которая является неизвестной. Поэтому следует выбрать аппроксимирующую функцию h(Ei,Y<n′>), с помощью которой ищется оптимальное приближение к разделяющей функции [7].
В алгоритмическом аспекте процедура обучения значительно упрощается, если применить разложение аппроксимирующей функции по ортонормированному базису G(Y) = (g1(Y), g2(Y),…,g n′(Y))т в соответствии с выражением
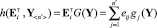, (5)
а в качестве меры отклонения аппроксимирующей функции от аппроксимируемой выбрать квадратичную меру
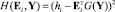. (6)
Далее базис G(Y) называется G-преобразованием вектора Y.
В работе [6] показано, что при выполнении условий (5) и (6) обучающая процедура представляется в виде рекуррентного соотношения
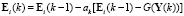, (7)
где ak, (k = 1,2,…) – элемент последовательности положительных чисел, удовлетворяющий условиям
.
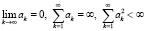Наиболее простым примером такой последовательности является гармонический ряд
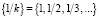. (8)
С учётом (8) рекуррентное соотношение (7) принимает вид
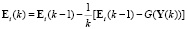, (9)
а для каждой координаты eij вектора Ei соотношение представляется как
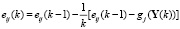. (10)
По мере увеличения числа шагов изображение Ei стремится к своему оптимальному значению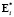 
с вероятностью единица:
.
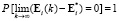Каждый из векторов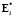 
может трактоваться и как точка в n′-мерном евклидовом пространстве Y, и как набор весовых коэффициентов уравнения гиперплоскости, отделяющей данное подмножество Yi от других подмножеств в пространстве Y. Очевидно, что каждая координата eij (
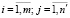) показывает степень сходства наблюдаемых состояний по j-му контролируемому признаку.
При реализации процесса обучения на основе рекуррентного соотношения (9) фактически решается градиентное уравнение
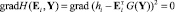. (11)
Уравнение (11) решается методом последовательных приближений. На каждом шаге используются данные из обучающей выборки (4) [7].
Группировка обучающих образов ДГУ СГЭП и ранжирование групп
Пусть Yi – подмножество обучающих образов технических состояний, соответствие которых i-му отказу ДГУ СГЭП системы известно. В данном подмножестве выделяется группа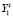 
, которая включает наибольшее количество неразличимых между собой элементов. Один из этих элементов 
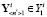после G-преобразования принимается в качестве вектора начального приближения: 
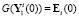. Элементы считаются неразличимыми, если их одноимённые координаты отличаются друг от друга на величины, сопоставимые с погрешностями регистрации соответствующих траекторий в контрольных точках системы. Во вторую группу 
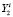входит не больше неразличимых элементов, чем в первую, и не меньше, чем в остальные. В третьей группе 
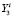количество неразличимых между собой элементов не больше, чем во второй, и не меньше, чем в остальных. Аналогичным образом формируются все группы [7].
Если через J обозначить индексное множество обучающих образов (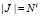
, где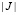 
– мощность множества J), соответствующих i-му отказу ДГУ СГЭП, то результаты их группировки и ранжирования полученных групп можно представить следующим образом:
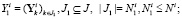
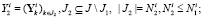
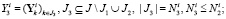(12)
…………………………………………..
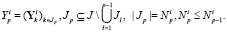
Порядок использования групп в ходе обучения совпадает с их номером (рангом), а последовательность применения обучающих образов в рамках одной и той же группы произвольна. Указанные действия выполняются для каждого подмножества Yi (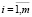
) из обучающей выборки (4).
Изложенный способ группировки и ранжирования означает задание на множествах Yi (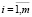
) отношений эквивалентности Σi, которые обеспечивают объединение в рамках одной группы неразличимых (эквивалентных) между собой элементов, а затем ранжирование групп по убыванию количества содержащихся в них образов. В результате из обучающей выборки по каждому отказу ДГУ СГЭП формируется упорядоченное фактор-множество 
, 
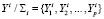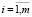, элементы которого удовлетворяют соотношениям (12).
Обучение с группировкой и ранжированием обеспечивает максимальное влияние на формирование изображений тех образов, которые наиболее характерны для соответствующих отказов ДГУ СГЭП. Данное утверждение объясняется тем, что коэффициент 1/k в соотношениях (9) и (10) на предыдущем шаге обучения больше, чем на последующем. Поэтому каждый предыдущий образ более значим, чем последующий [7].
Модификация обучающей процедуры
Если ДГУ СГЭП находятся в стадии разработки или эксплуатируются в единичных экземплярах и непродолжительное время, то объем и качество априорной информации об объекте исследования могут оказаться недостаточными даже для приближенной оценки диапазонов значений контролируемых показателей при различных отказах. В этом случае наиболее конструктивным является подход, основанный на информации о фактах выхода значений контролируемых показателей ДГУ СГЭП за допустимые интервалы
, 
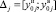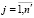, (13)
соответствующие удовлетворительному (работоспособному) состоянию системы (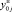
, 
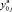– соответственно нижнее и верхнее допустимые значения j-го контролируемого показателя). При реализации предлагаемого подхода целесообразно использовать бинарные значения контролируемых показателей, определяемые выражением [7]
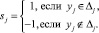(14)
В качестве базисных функций gj(Y), которые используются в рекуррентных соотношениях (9) и (10), могут быть приняты функции
gj(Y) = sjδj,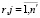 
, (15)
где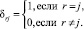 
– символ Кронекера.
Анализ в соответствии со схемой, изложенной в работе [8], показывает, что функции {gj(Y)|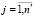
} вида (15) образуют полную систему ортонормированных функций. Из выражений (14) и (15) следует, что r-я базисная функция при r = j определяется как gj(Y) = sj. Тогда ортонормированный базис представляет собой вектор значений контролируемых показателей в бинарной форме: G(Y) = (s1, s2,…,sn′)т = S. Произвольное наблюдаемое состояние Yi, соответствующее i-му отказу, преобразуется аналогично: G(Yi) = (si1, si2,…,sin′)т = Si. Аппроксимирующая функция (5) записывается в форме
.
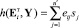Рекуррентное соотношение (9) принимает вид
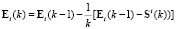. (16)
Изображения, полученные в соответствии с выражением (16), представляются как векторы нормализованных показателей
Ei = (ei1, ei2,…, eij,…, ein′)т,
eij∈[– 1,1],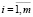 
. (17)
Положительное значение показателя eij указывает на то, что в обучающей выборке преобладают отказы, при которых значения j-го контролируемого показателя не выходят из допустимого интервала (13), и наоборот в случае отрицательного значения [7].
Выбор минимального множества контролируемых показателей
В общем случае размерность вектора Y<n’> наблюдаемого состояния ДГУ является избыточной. Это означает, что существует такой вектор контролируемых показателей Y<n> меньшей размерности (n < n’), на котором все отказы являются наблюдаемыми.
Далее рассматривается процедура формирования минимального множества контролируемых показателей, связанная со сжатием изображений (1) или (17) отказов ДГУ СГЭП. Предлагаемая процедура позволяет выявлять и исключать малоинформативные контролируемые показатели [7].
Известно [9], что минимальная различимость двух векторов одинаковой размерности обеспечивается при условии их линейной независимости. Причем степень различимости увеличивается при возрастании меры обладания ими свойством ортогональности. Следовательно, для обеспечения наблюдаемости отказов требуется два условия.
1. Матрица E транспонированных векторов изображений Ei (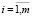
) не должна содержать одинаковых или пропорциональных строк: Ei ≠ а1Ek, ∀а1 ≠ {R\0}, 
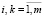, i ≠ k, где R – множество вещественных чисел. Данное условие указывает на линейную независимость строк матрицы E.
2. Значение скалярного произведения векторов Ei и Ek должно стремиться к нулю: (Ei, Ek) > 0,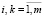 
, i ≠ k. Чем ближе к нулю значение скалярного произведения, тем больше мера обладания векторами Ei и Ek свойством ортогональности.
В зависимости от требований к достоверности контроля технического состояния необходимо задаваться некоторым пороговым значением а2, чтобы выполнялось условие
(Ei, Ek) < а2,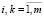 
, i ≠ k, а2∈R+ , (18)
где R+– множество положительных вещественных чисел.
С целью вывода правила для задания а2 и определения минимального состава контролируемых признаков, следует рассмотреть механизм получения ортогональных систем векторов при условии, что имеются исходные линейно независимые, но не ортогональные системы. К ним относится и система векторов E1, E2, …,Em. Наиболее эффективным способом решения подобных задач является процедура ортогонализации Грама – Шмидта [9]. Она позволяет путем линейного преобразования системы E1, E2,…,Em получить ортогональную систему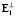 
, 
,…,
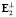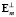, если общее число векторов m меньше их размерности n’: m < n’. С помощью указанной процедуры связь между исходными и преобразованными векторами задается следующими выражениями:
, 
,
,…,
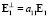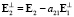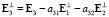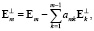(19)
где
а11 = 1,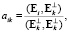 
, 
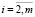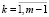. (20)
Из выражений (19) очевидно, что всякий вектор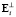 
ортогональной системы представляет собой некоторую линейную комбинацию векторов E1, E2,…,Em и, следовательно, является ненулевым. В противном случае оказались бы линейно зависимыми векторы E1, E2,…, Em, что не соответствует начальному условию.
Векторы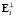 
(
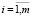) образуют матрицу 
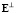, которая связана с исходной матрицей Е соотношением 
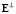= АЕ. Оператор преобразования А является левой треугольной матрицей, диагональные элементы которой равны единице, а внедиагональные определяются по формулам (20), т.е.
. (21)
Матрица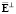 
, составленная из скалярных произведений вида 
, 
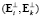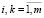называется матрицей Грама. Определитель этой матрицы (определитель Грама) имеет вид [7]
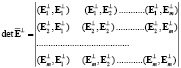. (22)
Все внедиагональные элементы определителя (22) равны нулю:
, 
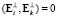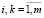, i ≠ k, (23)
поскольку векторы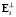 
и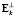 
ортогональны. Для диагональных элементов справедливо неравенство
, 
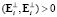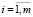, (24)
так как в матрице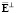 
нет нулевых строк. По этой причине 
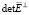> 0, следовательно, ранг матрицы 
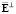равен m:
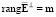. (25)
В работе [10] показано, что если матрица Грама системы векторов E1, E2,…,Em имеет ненулевые ведущие миноры и в каждой i-й строке данной матрицы диагональный элемент имеет наибольшее значение среди всех других элементов данной строки, то справедливы следующие утверждения [7].
1. Существует n таких координат (m ≤ n < n’), что сформированные из них векторы Ei = (ei1, ei2,…, ein)т,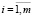 
будут попарно ортогональны.
2. Для обеспечения ортогональности не требуется линейного преобразования исходной системы векторов E1, E2,…,Em, так как матрица преобразования вырождается в единичную матрицу. Если в качестве линейного преобразования применяется процедура Грама – Шмидта, то в единичную обращается матрица (21).
Следовательно, для обеспечения наблюдаемости всех отказов системы на множестве из n контролируемых показателей необходимо и достаточно, чтобы выполнялись условия:
1) Мв ≠ 0, где Мв – ведущие миноры матрицы Грама;
2 (Ei, Ei) > (Ei, Ek),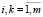 
, i ≠ k.
Первое условие выполняется, так как справедливо равенство (25). Второе условие выполняется в силу справедливости (23), (24) и (25) [2]. Данное условие можно использовать при задании порогового значения а2 в неравенстве (18): а2 = min{(Ei, Ei)},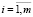 
.
Таким образом, из исходного множества контролируемых признаков может быть выбрано n (m ≤ n < n’) таких, которые обеспечивают наблюдаемость всех отказов системы. Практически должен быть реализован случай, когда n = m, поскольку именно в этом случае достигается минимально возможное множество контролируемых показателей [7].
Заключение
Адекватное математическое описание отказов по основным рабочим диагностическим признакам ДГУ СГЭП наряду с использованием минимального множества информативных контролируемых показателей является одним из ключевых условий повышения достоверности и оперативности принятия решений о фактическом состоянии и функциональной пригодности ДГУ СГЭП, а следовательно, повышения надежности работы всей системы электроснабжения наземных комплексов космического назначения.