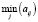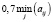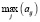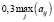Очевидно, что сельскохозяйственная отрасль экономики России переживает трудные времена. Обрушившиеся цены на нефть, санкции, а отсюда и трудности с импортозамещением, негативно влияют на сельское хозяйство нашей страны и экономику в целом. Также не нужно забывать о том, что на данный момент западные страны настороженно относятся к РФ: теперь уже бывшие экономические партнеры не идут на сотрудничество, сократились поставки продуктов и сырья, потерян интерес к продукции российского производства [3].
На фоне всего вышеперечисленного очевидно, что агропромышленный комплекс России сталкивается с целым рядом трудно- разрешимых проблем. Основные из них:
– недостаточное финансирование государственных программ для поддержания сельского хозяйства;
– вымывание оборотных средств: денег сельских хозяйств, которые поступают от реализации произведенной в отчётном году продукции, недостаточно для закупок дорожающей техники, семян, ГСМ и минеральных удобрений;
– дефицит кредитных ресурсов. Точнее, кредитные ресурсы доступны для аграриев, но процентные ставки – неподъемны;
– дефицит финансовых ресурсов приведет к сокращению закупок сельскохозяйственной техники.
Есть все-таки один положительный момент для сельского хозяйства во всей сложившиеся ситуации. В сегменте реального сектора экономики сельское хозяйство остается одной из наиболее привлекательных отраслей для инвестиций [2]. Можно отложить покупку, скажем, нового автомобиля на год, но нельзя отложить покупку мяса, хлеба и овощей на столь же длительный период. Также по прогнозам аналитиков можно сделать предположение, что в будущем данную отрасль ожидает подъем, а следовательно, чтобы в дальнейшем получать большую прибыль, необходимо развивать или начинать производство продукции сельского хозяйства уже сейчас [1].
В данной работе рассматривается вопрос о том, с производства какой продукции лучше начать создание и развитие малого бизнеса в сельскохозяйственной отрасли (а именно, выращивание овощей) и какое поведение помогает уменьшить убытки.
Этот бизнес был популярен и ранее. Не утратив своей актуальности и сегодня, он, напротив, идеально вписался в «корзину потребительских интересов» благодаря экологичности своей конечной продукции. Мода на здоровый образ жизни, правильное питание и отказ от вредных привычек выгодно оборачивает взор потенциальных клиентов в сторону такой группы товаров, как свежая зелень и овощи именно отечественного производства [3].
Постановка задачи
Рассмотрим следующие альтернативы, производство которых подходит для начальной стадии развития малого бизнеса [4].
Первая альтернатива – производство клубнеплодов, к которым относятся картофель, батат, топинамбур и др. Картофель является самой распространенной овощной культурой, занимая одно из первых мест в питании. Его справедливо называют вторым хлебом.
Вторая альтернатива – производство томатных овощей (помидоры, баклажаны, перец). Эти растения теплолюбивые и требуют хорошего полива. Существует два способа выращивания данного продукта: на открытом грунте и в теплицах. Производство на открытом грунте является процессом сезонным и быстро окупаемым, но существует риск, что не удастся заключить договор на поставку товаров и он пропадет, то есть существует риск получения убытка вместо прибыли. Выращивание томатов в теплицах является более рентабельным, но для этого нужен большой стартовый капитал, что, несомненно, является большим минусом.
И третья альтернатива – пряные овощи (укроп, петрушка, зеленый лук, сельдерей и т.д.). Эти растения особо не прихотливые к окружающей среде, легко транспортируемые и не требуют большого первоначального капитала для начала производства. Также их отличительные черты: экологичность, быстрая окупаемость, отсутствие сезонности и доступность для потребителя.
Для определения выбора альтернативы обратимся к математике, а именно, к теории игр. Экономико-математические методы и, в частности, теория игр широко применяются в экономике при исследовании рынка. Ранее авторам удалось применить экономико-математические методы в задаче моделирования и прогнозирования спроса на автомобили в России [5]. В настоящей работе на основе теории игр найдены оптимальные стратегии в задаче о производстве сельскохозяйственной продукции.
Введем ряд понятий.
Игра – это математическая модель конфликтной ситуации.
Игроки в игре – стороны, участвующие в конфликте.
Выигрыш – исход конфликта. Обычно он задается количественно, например, 1; – 5; 0.
Стратегии игрока – совокупность правил, определяющих выбор игрока при личном ходе в зависимости от ситуации.
Решение игры – выбор каждым игроком стратегии, которая удовлетворяет условию оптимальности, то есть один игрок должен получить максимальный выигрыш, в то время как другой придерживается своей стратегии. В то же время другой игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными.
Решить игру – это означает найти цену игры и ее оптимальное решение.
Построение модели и примеры её реализации
Возвращаемся к нашей проблеме и введем обозначения. Мы – игрок A, у нас имеется три стратегии: A1 – выбор альтернативы номер один, A2 – два, A3 – три. Так как выращивание овощей будет происходить на открытом грунте, одним из влияющих факторов окажется состояние природы. Введем второго игрока B – природу. Его стратегии: B1 – засушливое лето, B2 – дождливое лето, B3 – лето с переменными осадками. Таким образом, одной из сторон выступаем мы, сельскохозяйственное предприятие, заинтересованное в том, чтобы получить наибольший доход, а с другой стороны – природа, способная навредить нам в максимальной степени (от нее зависят погодные условия). В качестве выигрыша игрока A возьмем прибыль от реализации того или иного варианта (млн руб.) и будем считать, что расчеты прибыли зависят от состояний природы. Запишем их в виде матрицы, где строки – это стратегии игрока A, столбцы – стратегии игрока B:
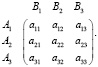
Все значения элементов матрицы получили методом экспертной оценки:
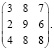
Эта матрица называется платежной матрицей или матрицей игры.
Найдем цену игры. Выделим минимальное значение матрицы в каждой строчке и выберем из них максимальное. Это будет минимальная цена игры, она обозначается как α
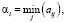
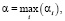
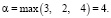
α = 4 – это гарантированный выигрыш игрока A.
Также найдем максимальную цену игры β. Для этого находим максимальное значение в каждом столбце и выбираем из них минимальное значение.
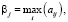
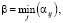
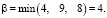
β = 4 – это гарантированный выигрыш игрока B.
Если α = β, как в нашем случае, то их значение – это чистая цена игры. Стратегии, соответствующие ей, называются оптимальными, а их совокупность – оптимальным решением игры.
Таким образом, можно сделать вывод, что оптимальным решением для игрока A будет выбор третьей стратегии, а именно, производство пряных овощей.
Но, как известно, природа действует совершенно случайно, и нет уверенности, что будет выбрана та или иная стратегия. Для подтверждения или опровержения сделанного нами выбора рассчитаем критерии оптимальности, которые учитывают то, что выбор игрока B (природы) имеет вероятностный характер.
Для определения критериев оптимальности нам понадобятся дополнительные данные, а именно вероятность наступления той или иной альтернативы и матрица рисков.
Методом экспертной оценки мы определили вероятность наступления стратегий игрока B:
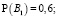
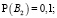
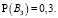
Значение риска определяется по следующей формуле:
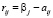 , где
, где 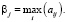
Таким образом, получаем матрицу рисков:
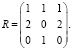
Теперь перейдем непосредственно к расчетам критериев оптимальности.
1. Критерий Байеса
Все необходимые данные запишем в виде таблицы.
Таблица 1
|
B1 |
B2 |
B3 |
¯ai |
αi |
|
|
A1 |
3 |
8 |
7 |
4,7 |
3 |
|
A2 |
2 |
9 |
6 |
3,9 |
2 |
|
A3 |
4 |
8 |
8 |
5,6 |
4 |
|
Рi |
0,6 |
0,1 |
0,3 |
||
|
βi |
4 |
9 |
8 |
||
где ai – средний выигрыш игрока A, который рассчитывается по формуле
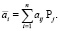
По критерию Байеса необходимо выбрать максимальное значение среднего выигрыша. В нашем случае оптимальной будет стратегия A3, так как при ней средний выигрыш достигает
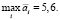
2. Критерий Вальда
Оптимальной по критерию Вальда считается стратегия, позволяющая игроку A получить нижнюю цену игры. Значение α мы уже рассчитывали, ее значение равно 4 и достигается при выборе игроком A стратегии A3.
3. Критерий Севиджа
Для данного критерия составим таблицу рисков.
Таблица 2
|
B1 |
B2 |
B3 |
ri |
|
|
A1 |
1 |
1 |
1 |
1 |
|
A2 |
2 |
0 |
2 |
2 |
|
А3 |
0 |
1 |
0 |
1 |
где ri – максимальное значение рисков из строки.
Таблица 3
|
B1 |
B2 |
B3 |
|
|
|
|
hi |
|
|
A1 |
3 |
8 |
7 |
3 |
2,1 |
8 |
2,4 |
4,5 |
|
A2 |
2 |
9 |
6 |
2 |
1,4 |
9 |
2,7 |
4,1 |
|
A3 |
4 |
8 |
8 |
4 |
2,8 |
8 |
2,4 |
5,2 |
По критерию Севиджа оптимальной считается та стратегия, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации, т.е.
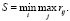
Таким образом, оптимальными по данному критерию считаются стратегии A1 и A3, так как
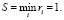
4. Критерий Гурвица
По этому критерию выбирается стратегия, при которой достигается максимальное значение величины:
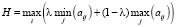 ,
,
0 ≤ λ ≤ 1,
где λ – коэффициент, который мы задаем сами, причем чем больше у нас желание подстраховаться, тем ближе значение к 1.
Мы возьмем λ = 0,7 и запишем для удобства расчетов все промежуточные результаты в табл. 3.
По этим данным видно, что H принимает максимальное значение 5,2 при стратегии A3.
По совокупности всех критериев делаем вывод, что стратегия A3 – оптимальная для руководства сельскохозяйственного предприятия, то есть следует заняться выращиванием пряных культур.
Возможное поведение фирмы при наличии больших убытков
Во многих практически важных конфликтных ситуациях в бизнесе, располагая той или иной информацией, стороны-участницы совершают свой выбор не раз и навсегда, а последовательно во времени, шаг за шагом. Тем самым они используют стратегии, отражающие как динамику конфликта, так и степень собственной осведомленности о фактически складывающейся обстановке в развитии этого конфликта.
Одним из классов игр, описывающих конфликты, динамика которых оказывает влияние на поведение участников, являются так называемые позиционные игры.
Позиционная игра – это бескоалиционная игра, моделирующая процессы последовательного принятия решений игроками в условиях меняющейся во времени и неполной информации. Процесс самой игры состоит в последовательном переходе (в период неопределенности) от одного состояния игры к другому состоянию, который осуществляется либо путем выбора игроками одного из возможных действий в соответствии с правилами игры, либо случайным образом (случайный ход).
Рассмотрим следующую ситуацию:
В Волгоградской области Южного федерального округа действует фирма-монополист «Y», занимающаяся производством и переработкой овощей. Наша фирма «Х» терпит серьезные убытки, так как в качестве стартового капитала были взяты кредиты.
1-й ход делает фирма В, т.е. «Y» предлагает полностью выкупить фирму с кредитами (1), либо выкупить только фирму (2), а долги останутся.
2-й ход делает фирма А, т.е. наша фирма: выбирает согласиться (1), либо отказаться (2).
Представим последовательность ходов в виде дерева игры:
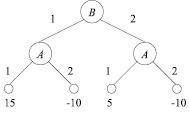
Запишем результаты расчетов в виде таблицы выигрышей игрока А и в виде матрицы игры:
Таблица 4
|
А1 |
A2 |
A3 |
A4 |
|||
|
(1,1) |
(1,2) |
(2,1) |
(2,2) |
|||
|
B1 |
1 |
W(1,1) 15 |
W(1,1) 15 |
W(1,2) – 10 |
W(1,2) – 10 |
|
|
B2 |
2 |
W(2,1) 5 |
W(2,2) – 10 |
W(2,1) 5 |
W(2,2) – 10 |
|
По рассмотренному выше алгоритму находим верхнюю и нижнюю цены игры. Как и в прошлый раз, их значение совпадает: α = β = – 10.
Таким образом можно сделать вывод, что для игрока В выгоднее не покупать нашу фирму, тогда мы понесем убыток в 10 млн руб. и разоримся, тем самым«Y» избавляется от потенциального конкурента и остается монополистом в этой области.
Выводы
Используя теорию игр, мы выяснили, что для создания малого бизнеса в сельскохозяйственной отрасли лучше начинать с производства пряных овощей. Также мы смоделировали ситуацию, в которой мы несем убытки, и возможное поведение наших конкурентов.
Сельскохозяйственная отрасль является наиболее перспективной в экономике России. Теория игр нашла широкое применение в инновационной экономике. В последние годы ее значение существенно возросло во многих областях экономических и социальных наук. В экономике она применима не только для решения общехозяйственных задач, но и для анализа стратегических проблем предприятий, что способствует выбору направления основного производства, принятию оптимальных управленческих решений. Применение теории игр способствует успешному развитию бизнеса.