Для системы векторных уравнений вида: 
, где К, D – векторы конвективных и диффузионных слагаемых уравнений, рассматривается следующее преобразование и решение. После дифференцирования и изменения знака левой и правой части, справедлива форма: 
которая без труда может быть представлена в виде следующей трехточечной аппроксимации:
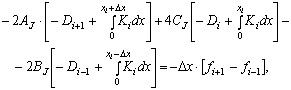(1)
где i – сеточный индекс ячейки в области определения функций; J – номер уравнения.
Обозначая через вектор-столбец Yi выражения в квадратных скобках сеточного уравнения (1) и через Fi – выражения в правой части, получим: 
с граничными условиями:
при i = 0: 
при i = N: 
где A, B, C – квадратные матрицы коэффициентов.
Общая схема алгоритма численного решения системы неоднородных уравнений приводится к последовательности действий схемы метода матричной прогонки. Согласно данной схемы, решение задачи в методе матричной прогонки ищется в виде:
(2)
где α, β – матрица и вектор, составленные из неизвестных коэффициентов прогонки, определяемые рекуррентными зависимостями вида:
. (3)
В отличии от известных подходов, алгоритм (2,3) реализуется не для физических переменных задачи, а для их комбинации – выражений в квадратных скобках сеточного уравнения (1), что составляет первый этап вычислительного цикла. Определение искомых функций задачи проводится с применением любой итерационной схемы на втором этапе.