Оптимальное управление сложными нелинейными объектами имеет большой теоретический и практический интерес. В целом задача синтеза оптимальных систем управления в теоретическом плане в общем виде решена [13], однако формирование управления, например, по критерию максимального быстродействия в замкнутом виде выполнено только для объектов, математические модели которых описываются уравнениями невысокого порядка.
Основной проблемой является необходимость решения краевых задач и наличие ограничений на управление. В случае нелинейных систем – разнообразие видов нелинейностей. Универсального подхода нет. Эти особенности приводят к необходимости в каждом конкретном случае разрабатывать свой метод решения задачи. Разработано множество методов, имеющих свои достоинства и недостатки [1–3, 10, 14, 15]. Список крайне неполон. Предлагается один из возможных подходов к решению задачи. Он основан на аппарате матричных операторов.
Аппарат матричных операторов нашел свое широкое применение для решения самых различных задач при исследовании и проектировании систем управления [5–7, 11, 12]. Его применение совместно с другими методами позволяет существенно расширить круг решаемых задач. Одной из таких является задача синтеза оптимальных по быстродействию программных управлений для нелинейных объектов. Желательно иметь решение задачи в замкнутом виде, однако это не всегда возможно. Если найдено оптимальное программное управление, то задача синтеза регулятора для нелинейного объекта упрощается. Она сводится, например, к задаче стабилизации движения объекта относительно программной траектории и программного управления, так называемая задача двухэтапной оптимизации [12].
В работе предлагается использовать аппарат матричных операторов совместно с абстрактной конечномерной L-проблемой моментов М.Г. Крейна и А.А. Нудельмана [8]. В работе [9] Е. Крейндлер показал, как можно использовать положения L – проблемы моментов для синтеза оптимального по быстродействию управления для класса линейных объектов.
Применение линеаризации Ньютона – Канторовича, в продолжение развития идей Е. Крейндлера, позволяет для нелинейных объектов также синтезировать оптимальное по быстродействию программное управление.
Постановка задачи. Задан объект, описываемый уравнением вида
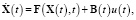 (1)
(1)
где 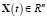 ,
, 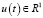 .
.
Полагаем, что объект является вполне управляемым. Необходимо синтезировать скалярное управление u(t), переводящее объект из заданного начального состояния X(t0) в конечное состояние X(T) и доставляющее минимум следующему функционалу
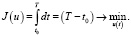 (2)
(2)
Алгоритм синтеза
Алгоритм состоит из следующих основных этапов.
1. Линеаризация нелинейной математической модели объекта по схеме Ньютона – Канторовича.
2. Преобразование дифференциальных уравнений к форме с матричными операторами.
3. Синтез управления, согласно заданному критерию с использованием L-проблемы моментов.
4. Организация итерационного процесса, согласно схеме Ньютона – Канторовича.
Линеаризация нелинейной математической модели
Данная процедура достаточно подробно рассмотрена [6, 7, 11] и в других работах автора, посвященных задачам синтеза. Отметим лишь, что в процессе линеаризации осуществляется переход от нелинейных дифференциальных уравнений (1) к последовательности линеаризованных уравнений вида
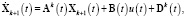 (3)
(3)
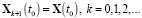 ,
,
где
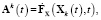
 (4)
(4)
Матрица 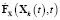 определена следующим образом:
определена следующим образом:
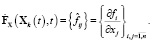 (5)
(5)
Линеаризованные дифференциальные уравнения (3) имеют переменные коэффициенты. Их структура соответствует той, с которой обычно выполняется синтез управления для неавтономных объектов.
Преобразование дифференциальных уравнений к необходимой форме
Преобразование дифференциальных уравнений в форму необходимую для применения L-проблемы моментов осуществляется переходом к системе интегральных моментных соотношений и систему моментов.
Для этого перейдем от дифференциального уравнения (3) к интегральному уравнению Фредгольма 2 – рода (индекс k для краткости записи опустим):
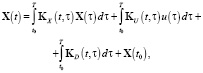
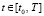 , (6)
, (6)
где матричные ядра 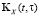 ,
, 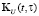 ,
, 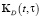 имеют вид
имеют вид
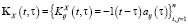 ,
,
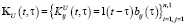 ,
,
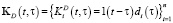 .
.
Представим сигналы X(t), X(t0), u(t) и ядра уравнения (6) 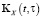 ,
, 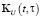 ,
, 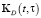 в виде конечномерного разложения по заданному ортогональному базису
в виде конечномерного разложения по заданному ортогональному базису 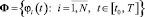 :
:
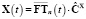 ,
, 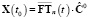 ,
,
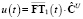 ,
,
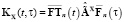 ,
,
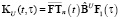 ,
,
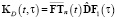 , (7)
, (7)
где 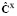 ,
, 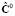 ,
, 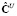 ,
, 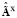 ,
, 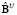 ,
, 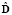 – спектральные характеристики соответствующих функций,
– спектральные характеристики соответствующих функций, 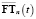 ,
, 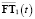 ,
, 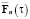 ,
, 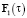 – клеточные матрицы, построенные на элементах ортогонального базиса.
– клеточные матрицы, построенные на элементах ортогонального базиса.
Теперь можно перейти от интегральной формы описания объекта к спектральной форме
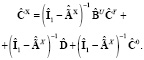
Если вновь вернуться во временную область, то имеет место следующая зависимость, связывающая управление с выходом:
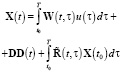 , (8)
, (8)
где
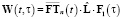 ,
,
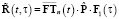 ,
, 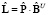 ,
,
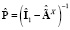 ,
, 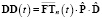 .
.
Выражение (8) можно записать также в виде
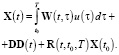 (9)
(9)
Здесь
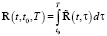 .
.
Полагая t = T, получаем систему моментных соотношений
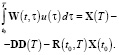 (10)
(10)
В зависимости (10) W(t, τ) – системой моментных функций, 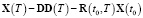 – система моментов.
– система моментов.
Синтез управления
Управление оптимальное u(t) по критерию (2) всегда ограничено. Это может быть ограничение по величине 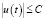 , по энергии
, по энергии 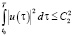 или по площади
или по площади 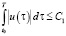 . Все они объединяются одним выражением
. Все они объединяются одним выражением
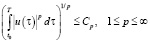 . (11)
. (11)
При p = ∞ и q = 1 имеет место ограничение управления по величине.
Левая часть неравенства (11) есть норма u(t) в пространстве Lp. Поэтому при синтезе управления можно воспользоваться методами функционального анализа. В [9] отмечается, что «управление будет оптимальным только в случае, если оно удовлетворяет неравенству (11) со знаком равенства». Кроме того для оптимальности управления необходимо и достаточно, чтобы оно максимизировало следующее выражение
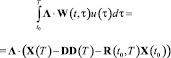 , (12)
, (12)
при некотором ненулевом векторе ∧.
Как видим, имеет место классическая вариационная задача – максимизация выражения (13) при ограничении (12), которое рассматривается, как равенство. Решение задачи известно – [11, 18]. Оптимальное управление определяется следующим выражением:
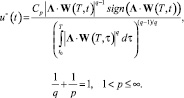 (13)
(13)
При условии
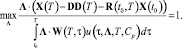 (14)
(14)
Как видим из (13), оптимальное управление является функцией времени и зависит от значений элементов ненулевого вектора – ∧, минимального времени – T и величины ограничения – Cp: 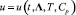 .
.
Для значений p = ∞ и q = 1 имеет место известный результат [8, 13]
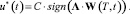 (15)
(15)
С учетом вида управления (15), условие (14) становится следующим:
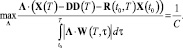 (16)
(16)
Если длину вектора ∧ выбрать произвольно, например, так, чтобы
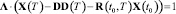 , (17)
, (17)
то условие (17) упрощается:
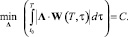 (18)
(18)
Выражение (18) есть решение поставленной задачи на максимальное быстродействие.
Наименьшее T, которое удовлетворяет данному уравнению для заданного значения C при условии (17) есть искомое минимальное время для текущего шага итерационного процесса.
Организация итерационного процесса
Линеаризация по схеме Ньютона – Канторовича предполагает организацию итерационного процесса по уточнению решения уравнения (3) до тех пор, пока решение линеаризованного уравнения не будет близко к решению исходного нелинейного уравнения. Как правило, начальные приближения выбираются исходя из некоторых практических соображений, например, при решении данной задачи в качестве них можно использовать начальные состояния, из которых переводится объект. На текущем шаге итерационного процесса находится система моментных функций – W(t, τ) и система моментов – 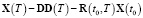 (смотри систему моментных соотношений (10)), находится оптимальное время управления T, удовлетворяющее уравнению (18) и искомое управление u(t). Найденному управлению соответствует своя фазовая траектория, являющаяся основой для следующего шага итерационного процесса. Итерационный процесс продолжается до тех пор, пока с заданной точностью не будет выполнено ограничение на управление и не будет меняться время управления T.
(смотри систему моментных соотношений (10)), находится оптимальное время управления T, удовлетворяющее уравнению (18) и искомое управление u(t). Найденному управлению соответствует своя фазовая траектория, являющаяся основой для следующего шага итерационного процесса. Итерационный процесс продолжается до тех пор, пока с заданной точностью не будет выполнено ограничение на управление и не будет меняться время управления T.
Пример. Объект управления описывается уравнением
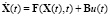 ,
,
где 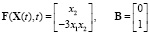 .
.
Требуется синтезировать управление, переводящее объект из начального состояния 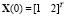 в конечное состояние
в конечное состояние 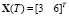 за минимальное время при ограничении на управление
за минимальное время при ограничении на управление 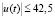 .
.
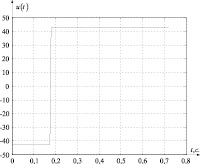
Рис. 1. Управление u(t)
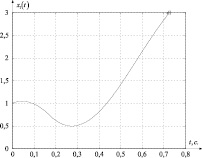
Рис. 2. Изменение координаты x1(t)
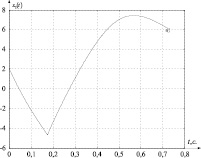
Рис. 3. Изменение координаты x2(t)
Начальные приближения 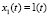 ,
, 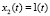 . Найденное время управления T = 0,7216256 с. Полученное конечное состояние:
. Найденное время управления T = 0,7216256 с. Полученное конечное состояние: 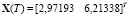 . Ограничение на управление:
. Ограничение на управление: 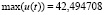 . Данная точность получена за 4 итерации.
. Данная точность получена за 4 итерации.
На рис. 1 показан график изменения управления; на рис. 2–3 графики изменения фазовых координат. На рис. 2–3 точками показаны точные конечные значения фазовых координат.
Заключение
Предложен на взгляд автора, достаточно эффективный и конструктивный метод синтеза оптимальных по быстродействию программных управлений для нелинейных объектов. Приведенный пример свидетельствует о том, что управление является ограниченным и обеспечивает перевод объекта из заданного начального состояния в заданное конечное состояние за минимальное время.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Калужской области (грант № 16-41-400701).



