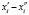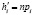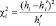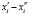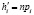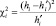Исследование переходных процессов (ПП) синхронных машин (СМ) из опытов внезапного симметричного короткого замыкания (ВКЗ), гашения поля (ГП), восстановления напряжения (ВН), ударного возбуждения (УВ) и других невозможно с полным объёмом генеральной совокупности (ГС) случайного признака переходной составляющей симметричного тока (напряжения) якоря, из-за наличия сверхпереходной составляющей, которая затухает (возрастает) с меньшей постоянной времени (ПВ) в сравнении с ПВ переходной составляющей. От влияния различных случайных факторов эти составляющие отклоняются от экспоненциального затухания (возрастания) с появлением разброса ПВ в широких пределах. Отсутствие эффективных и достоверных аналитических методов в классической математике затрудняют идентификацию этих составляющих. Решение данной проблемы с использованием классических методов теории вероятностей и математической статистики (ТВиМС) не всегда является эффективным и результативным.
Авторами разработаны новые вероятностно-статистические методы (ВСМ) идентификации зашумлённых ПП СМ с использованием элементов и методов ТВиМС [1–3]. При этом возникли трудности с использованием известных критериев с целью подтверждения распределения случайного признака по нормальному закону при идентификации переходной составляющей по зашумлённым ПП СМ. Одним из перспективных и надёжных критериев для подтверждения предполагаемого нормального закона случайного признака в ТВиМС является критерий согласия Пирсона (или χ2). Его привлекательность заключается в том, что, кроме своего основного назначения, он может быть использован одновременно для проверки достоверности того, что взятая партия случайного признака из выборки, незначительно отклоняющаяся от её математического ожидания (МО), распределена по биномиальному закону или закону Пуассона при распределении редких событий [4]. Это важное обстоятельство было использовано для минимизации объёма эффективных точечных выборок (ЭТВ) по контрольной партии выборки для оценки математического ожидания (МО) при неизвестных дисперсиях ГС.
Для решения проблемы разработан метод статистических исследований с целью поиска оптимальных оценок дисперсии и МО для переходной составляющей по зашумлённым ПП СМ в процессе их стендовых испытаний [6]. Программа статистических исследований включает выбор границ участка ПП СМ с одной переходной составляющей симметричного тока якоря для её исследования и идентификации; расчёт объёма ГС и выборки случайного признака на исследуемом участке с переходной составляющей; оценку уровня зашумленности переходной составляющей и степени отклонения случайного признака от экспоненциального затухания в исследуемом диапазоне ПП с использованием вариационных рядов по выборке; исследования, связанные с достоверной оценкой дисперсии случайного признака по выборке с проверкой гипотезы предполагаемого нормального закона распределения случайного признака с использованием критерия согласия Пирсона; минимизацию объема ЭТВ с использованием распределения Пуассона с оценкой уровня вероятности данного объёма; конструирование на базе минимизированного объема ЭТВ комбинаторных унифицированных выражений для исследования и идентификации переходной составляющей симметричного тока (или напряжения) якоря СМ.
Перед исследованиями ПП СМ в ВСМ предусмотрена процедура оптимизации установившегося значения симметричного тока якоря по опытным данным в исследуемом диапазоне 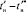 ПП с использованием ЭТВ, обоснованных на базовом случайном признаке в работе [2]:
ПП с использованием ЭТВ, обоснованных на базовом случайном признаке в работе [2]:
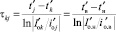 , (1)
, (1)
где 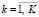 ,
, 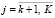 – переменные для задания нижней и верхней границ;
– переменные для задания нижней и верхней границ; 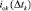 – элементы дискретного ПП;
– элементы дискретного ПП; 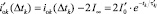 – дискретные величины между огибающими тока якоря на участке ПП с переходной составляющей,
– дискретные величины между огибающими тока якоря на участке ПП с переходной составляющей, 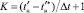 ,
, 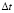 – шаг дискретизации, с; элементы дискретного ПП в узлах дискретизации с шагом 0,01 с рассчитываются по формуле, впервые полученной в работе [5]:
– шаг дискретизации, с; элементы дискретного ПП в узлах дискретизации с шагом 0,01 с рассчитываются по формуле, впервые полученной в работе [5]:
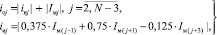 (2)
(2)
где 0,375; 0,75; 0,125 – выведенные коэффициенты на базе интерполяционной схемы Эйткена для дискретно заданных ПП с равномерным шагом дискретизации.
Постоянная времени  по выражению (1), принятая за базовый случайный признак, является точечной выборкой объёмом n = 2 и служит как для расчёта объёма ГС N по всему ПП, так и объёма выборки nв случайного признака в диапазоне
по выражению (1), принятая за базовый случайный признак, является точечной выборкой объёмом n = 2 и служит как для расчёта объёма ГС N по всему ПП, так и объёма выборки nв случайного признака в диапазоне 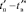 ПП с переходной составляющей по комбинаторному выражению
ПП с переходной составляющей по комбинаторному выражению
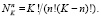 (3)
(3)
При наличии полных исходных данных генеральный ряд случайного признака конструируется по комбинаторному выражению
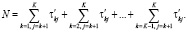 (4)
(4)
Рассчитывают МО 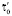 и дисперсию
и дисперсию 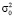 распределения случайного признака ГС:
распределения случайного признака ГС:
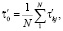
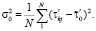 (5)
(5)
Выборка случайного признака nв конструируется с условием охвата всех элементов  на участке
на участке 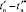 тем же комбинаторным подходом, что и ГС, с возможностью изменения объема в любую сторону:
тем же комбинаторным подходом, что и ГС, с возможностью изменения объема в любую сторону:
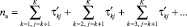 (6)
(6)
Вычисляют МО 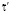 и дисперсию σ2 распределения выборки случайного признака nв
и дисперсию σ2 распределения выборки случайного признака nв
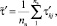
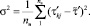 (7)
(7)
Исследованиями установлено, что использование МО и дисперсии по (6) и (7) при сильно зашумлённых ПП СМ в методике критерия Пирсона не срабатывает, так как при определении интервальной вероятности в методике на её значение решающее влияние оказывает величина дисперсии, приводящая к сильному отклонению гипотетических частот в интервалах разбиения исследуемой области случайного признака ПП. Исследования показали, что наиболее перспективным направлением в поисках оптимальной дисперсии случайного признака являются вариационные ряды, которые позволяют получать оценку разброса случайного признака R, характеризующую уровень зашумлённости ПП и коэффициента вариации v, связанного со степенью отклонения затухания ПП от экспоненциального закона по известным в теории ТВиМС формулам:
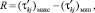
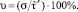 (8)
(8)
При работе с вариационными рядами приходится изменять объём выборки за счёт исключения нереальных случайных признаков, что ведёт к изменению МО и границ интервалов, которые в меньшей степени, но влияют на точность и трудоёмкость исследования. В литературе по ТВ и МС отсутствуют рекомендации по эффективному использованию коэффициентов вариации вариационных рядов случайного признака и других полезных рекомендаций. В представленных исследованиях предложено оригинальное решение возникающей проблемы, связанное с уточнением коэффициентов вариации вариационных рядов по выборке.
Исследованиями установлено, что снижение коэффициента вариации ниже определённого уровня положительно решает проблему использования критерия Пирсона. А использование ЭТВ, которые конструируются по формуле (1), с учётом коэффициента жёсткой связи между элементами ПП в нижней и верхней границах, обоснованному в [5]
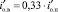 (9)
(9)
и отклоняются на минимальную величину с относительной погрешностью от МО выборки, а также легко из неё извлекаются. ЭТВ, сформированные по (1) и (9), в объёме выборки случайного признака по (6), образуют ядро их скопления в количестве, соответствующем первым 6–7 суммам в комбинаторном выражении (5), которые после усреднения и минимизации по распределению Пуассона [4] данного объёма с его вероятностной оценкой используются для оценки критерия Пирсона. При минимизации объёма ЭТВ задаются минимальным уровнем относительного отклонения ЭТВ от МО выборки для определения их процентного содержания δ в объёме ГС по (3) для расчёта величины 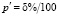 . Из вариационного ряда берут контрольную партию объёмом из четырёх ЭТВ nэф = 4с заданным минимальным отклонением от МО для расчёта величины
. Из вариационного ряда берут контрольную партию объёмом из четырёх ЭТВ nэф = 4с заданным минимальным отклонением от МО для расчёта величины 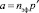 . Определяют вероятность нулевого появления ЭТВ с заданным минимальным отклонением от МО
. Определяют вероятность нулевого появления ЭТВ с заданным минимальным отклонением от МО 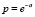 . Определяют вероятность появления в контрольной партии одной ЭТВ с превышением заданного минимального отклонения от МО
. Определяют вероятность появления в контрольной партии одной ЭТВ с превышением заданного минимального отклонения от МО 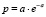 ; двух ЭТВ для
; двух ЭТВ для 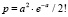 , трёх ЭТВ для
, трёх ЭТВ для 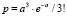 и т.д. Сумма полученных вероятностей в итоге должна равняться 1,0.
и т.д. Сумма полученных вероятностей в итоге должна равняться 1,0.
По результатам оценок вероятностей конструируют комбинаторное унифицированное выражение минимизированного объёма ЭТВ для проведения дальнейших исследований и идентификации переходной составляющей ПП в рассматриваемых опытах СМ (формулы представлены в работах [1, 2]). С помощью ЭТВ идентифицируют остальные составляющие ПП, которые позволяют по известным выражениям получать параметры СМ.
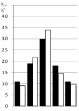
Апробация программы исследования ПП осуществлена на натурном образце СМ мощностью 800 кВт по результатам её стендовых испытаний в опыте ВКЗ с напряжением испытания, равного 1,05•Uн при Uн = 6 кВ. На рисунке, а для одной из фаз в столбцах 1, 2 представлена дискретная информация о переходной составляющей по формуле (2).

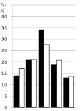
Гистограммы распределения критерия Пирсона: ¦ – эмпирическая частота; ? – гипотетическая частота
С целью исключения систематической погрешности, вносимой установившимся значением тока якоря, его оптимизация осуществлена по результатам опытных данных стендовых испытаний для всех фаз в исследуемых диапазонах ПП с одной переходной составляющей, например для рассматриваемой фазы С в диапазоне исследования 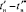 = 0,103 – 0,253 с по статистическому выражению
= 0,103 – 0,253 с по статистическому выражению
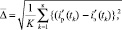 (10)
(10)
где 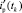 – расчётная модель переходной составляющей по усреднённым ЭТВ с учётом условия (9),
– расчётная модель переходной составляющей по усреднённым ЭТВ с учётом условия (9), 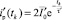 ;
; 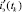 – экспериментальное значение переходной составляющей, очищенное от оптимизированного установившегося значения тока якоря,
– экспериментальное значение переходной составляющей, очищенное от оптимизированного установившегося значения тока якоря, 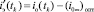 ; K – число элементов (т.е. дискретно заданных токов между огибающими) на участке переходной составляющей (столбец 2 на рисунке, а).
; K – число элементов (т.е. дискретно заданных токов между огибающими) на участке переходной составляющей (столбец 2 на рисунке, а).
При 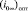 = 13,1 мм среднеквадратичная погрешность приближения
= 13,1 мм среднеквадратичная погрешность приближения 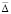 по (10) оказалась наименьшей с МО
по (10) оказалась наименьшей с МО 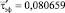 с и дисперсией σ2 = 4,0616683•10–6, полученные по усреднённым ЭТВ в указанном выше диапазоне. Нижняя граница tн задана равной 0,1 с из-за практически полного затухания сверхпереходной составляющей, а верхняя выбрана по превышению переходной составляющей над установившимся ПП в диапазоне 15–20 %. По формулам (1), (8) в обоснованном диапазоне исследования
с и дисперсией σ2 = 4,0616683•10–6, полученные по усреднённым ЭТВ в указанном выше диапазоне. Нижняя граница tн задана равной 0,1 с из-за практически полного затухания сверхпереходной составляющей, а верхняя выбрана по превышению переходной составляющей над установившимся ПП в диапазоне 15–20 %. По формулам (1), (8) в обоснованном диапазоне исследования 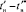 по исходным данным столбиков 1, 2 рисунка а создана выборка случайного признака объёмом из 120 членов ряда для исследования переходной составляющей (столбики на рисунке, а приведены не до конца).
по исходным данным столбиков 1, 2 рисунка а создана выборка случайного признака объёмом из 120 членов ряда для исследования переходной составляющей (столбики на рисунке, а приведены не до конца).
Генеральная совокупность случайного признака переходной составляющей по всему ПП до её полного затухания составляет около 600 членов ряда. При этом на переходную составляющую в исследуемом диапазоне приходится 95 % случайного признака от всего ПП, что оказалось вполне оправданным. Созданный по выборке вариационный ряд случайного признака (на рисунке, б) с разбросом его на 46 % и коэффициентом вариации 5,76 % не подтверждает нормальный закон по методике Пирсона. Только нормализация вариационного ряда с уменьшением его объёма до 101 члена позволила подтвердить предполагаемый нормальный закон распределения случайного признака. При этом коэффициент вариации снизился до 2,73 % с МО, равного 0,080401 с. Для эффективного снижения трудоёмкости исследований использовались ЭТВ. По рисунку, а видно, что в первых 6–7 суммах по формуле (6) находятся ЭТВ (выделенное ядро жирным шрифтом), полученные по формуле (1) с учётом условия (9), отклоняющаяся с минимальной относительной погрешностью от МО.
Важнейшим обстоятельством при этом явилось их практическое совпадение с МО вариационного ряда и постоянством их величины с незначительным отклонением от МО в пределах долей процента.
Среднее значение ЭТВ из 6 штук по первым суммам в формуле (6) составило величину, равную 0,080659 с. Таким образом, в объёме выборки из 120 случайных признаков во всех фазах обнаруживается ядро ЭТВ по формуле (6), содержащихся в первых 6–7 суммах. Поэтому при исследованиях переходной составляющей с целью точной её идентификации при наличии сильной зашумлённости ПП следует сразу обращаться к ядру ЭТВ для использования МО для расчёта критерия Пирсона, дисперсию при этом берут по нормализованному вариационному ряду. На рисунке г представлена гистограмма для исследуемой фазы. На рисунке дополнительно представлена результирующая информация по результатам исследуемого ПП фазы С, а для фаз А и В в табл. 1–3.
Таблица 1
Результаты исследований по вариационным рядам
|
Фаза |
n |
|
σ, с |
nн |
|
σ, с |
v, % |
nэф |
|
σэф, с |
p(nэф = 4) |
|
А |
120 |
0,079389 |
0,008164 |
89 |
0,078652 |
0,00299 |
3,80 |
7 |
0,078530 |
0,00299 |
0,9673 |
|
В |
120 |
0,084271 |
0,006249 |
101 |
0,083295 |
0,00230 |
2,76 |
6 |
0,083180 |
0,00230 |
0,9673 |
Таблица 2
Расчёт критерия Пирсона и гистограмма для фазы А
|
Фаза |
Интервал |
Границы интервала
|
Эмпирическая частота hi |
Интервальная вероятность рi |
Гипотетическая частота
|
|
|
|
А |
k1 k2 k3 k4 k5 |
– ∞ – 0,0810 0,0810 – 0,0825 0,0825 – 0,0841 0,0841 – 0,0857 0,0857 – + ∞ |
14 21 34 19 13 |
0,17105 0,21105 0,2733 0,20675 0,13785 |
17,27605 21,31605 27,6033 20,88175 13,92285 |
0,621235 0,004686 1,482350 0,169573 0,061169 |
|
|
∑ |
101 |
1,000 |
101 |
2,334327 |
|||
Таблица 3
Расчёт критерия Пирсона и гистограмма для фазы В
|
Фаза |
Интервал |
Границы интервала
|
Эмпирическая частота hi |
Интервальная вероятность рi |
Гипотетическая частота
|
|
|
|
В |
k1 k2 k3 k4 k5 |
– ∞ – 0,0748 0,0748 – 0,0774 0,0774 – 0,0804 0,0804 – 0,0823 0,0823 – + ∞ |
11 19 30 18 11 |
0, 0681 0,19955 0,4273 0,18805 0,117 |
6,8781 20,15455 33,1573 18,99305 11,817 |
0,65460 0,0661382 0,0786783 0,471664 0,0028339 |
|
|
∑ |
89 |
1,000 |
89 |
2,163068 |
|||
С учётом объёма случайного признака по всему ПП около 600 членов ГС, для контрольной партии ЭТВ из 5 шт. с отклонением от МО менее процента вероятность сохраняется достаточно высокой. При этом процентное их содержание составляет менее 1 %, точнее 5/600 = = 0,83 %. Тогда р’ = 0,83 %/100 % = 0,0083, а = 5×0,0083 = 0,0415 и вероятность р = е–а = 0,9593. При контрольной партии ЭТВ в объёме nэф = 4 вероятность р = е–а = 0,9673. При объёме nэф = 3 вероятность р = е–а = 0,9754. Это очень высокая вероятность минимизации объёма ЭТВ с заданной минимальной относительной погрешностью всех ЭТВ в контрольной партии. Поэтому в исследованиях с идентификацией переходной составляющей ПП СМ ВСМ конструирование формул с позиций практического удобства их программирования и использования при исследованиях минимизированного объёма ЭТВ принято равным четырём. В фазе С для контрольной партии объёмом nэф = 4 вероятность с нулевым отклонением от заданной минимальной погрешности от МО всех четырёх ЭТВ составила 0,9673. Отклонение от заданной погрешности одной ЭТВ соответствует вероятности равной 0,0257, двух – вероятность практически отсутствует – 0,0004, трёх – 0,0000. Вероятность отклонения ЭТВ с заданной минимальной погрешностью от МО одной ЭТВ имеет достаточно низкий уровень, для двух и более отклонение ЭТВ практически отсутствует. Сумма вероятностей по 2 первым слагаемым достигает высокого уровня – 0,9997 для всех фаз исследуемого ПП СМ.
Выводы
1. Предложен оригинальный способ снижения трудоёмкости исследований ПП СМ для высокоточной и достоверной их идентификации с учётом влияния на данные процессы различных случайных факторов.
2. По результатам исследования натурных испытаний СМ мощностью 800 кВт подтверждена высокая эффективность разработанной программы исследования зашумлённого ПП с целью обеспечения высокоточной и достоверной идентификации переходной составляющей симметричного тока якоря с использованием вариационных рядов случайного признака, критерия Пирсона, минимизированного объёма ЭТВ с помощью распределения Пуассона для редких случайных событий.
3. В соответствии с ТВиМС при неизвестных параметрах ГС случайного признака они могут быть получены по выборке из ГС и с достаточной точностью и вероятностью по ЭТВ с существенным снижением трудоемкости исследований.
Работа выполнена в рамках государственного задания Министерства образования и науки РФ № 13.832.2014/K «Разработка методологических основ адаптивного управления автономными и неавтономными газотурбинными электростанциями мощностью до 25 МВт».




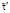 , с
, с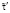 , с
, с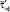 , с
, с