Блочный шифр «Кузнечик» представляет собой симметричный алгоритм блочного шифрования с размером блока 128 бит и длиной ключа 256 бит, для генерации которого используется сеть Фейстеля. Данный шифр вошел в состав стандарта ГОСТ Р 34.12-2015 «Информационная технология. Криптографическая защита информации. Блочные шифры», вступившего в силу с 1 января 2016 года.
Шифр «Кузнечик» представляет собой симметричный алгоритм блочного шифрования с размером блока 128 бит и длиной ключа 256 бит, для генерации которого используется сеть Фейстеля.
При реализации алгоритма шифрования используются преобразования, представленные в работе [3].
Алгоритм развертывания ключа использует итерационные константы Ci∈V128, i = 1, 2, …, 32, которые определены следующим образом:
Ci = L(Vec128(i)), i = 1, 2, …, 32.
Итерационные ключи Ki∈V128, i = 1, 2, …, 10, вырабатываются на основе ключа
K = k255||…||k0∈V256, ki ∈ V1, i = 0, 1, …, 255,
и определяются равенствами:
K1 = k255||…||k128;
K2 = k127||…||k0;
(K2i + 1, K2i + 2) = F [C8(i – 1) + 8]…F [C8(i – 1) + 1](K2i – 1, K2i), i = 1, 2, 3, 4.
Генерация раундовых ключей начинается с разбиения мастер-ключа пополам, так получается первая пара раундовых подключей (K1 и K2). Для генерации последующих пар применяется 8 раундов сети Фейстеля, каждый из которых использует функцию F и константу Cj, которая вычисляется путем применения линейного преобразования L к значению номера раунда. Чтобы выработать подключи K2i+1 и K2i+2, в сеть Фейстеля подаются предыдущие значения K2i-1 и K2i.. На вход функции F поступает значение подключа K2i, которое складывается по модулю два с константой Cj, проходит через табличную замену с помощью блока S и перемешивание информации с помощью преобразования L. Полученное на выходе функции F значение складывается по модулю два с подключом K2i-1, после сложения левая и правая часть меняются местами. Аналогично проходят оставшиеся 7 раундов, но только в 8 раунде части не меняются местами. Результат 8 раунда дает подключи K2i+1 – левая часть и соответственно K2i+2 – правая часть. Для шифрования/расшифрования необходимо 10 раундовых подключей, так как после завершения 8 раундов сети Фейстеля получается 2 раундовых подключа, то схему нужно применить 4 раза.
Алгоритм шифрования в зависимости от значений итерационных ключей Ki∈V128, i = 1, 2, …, 10, реализует подстановку EK1, …, K10, заданную на множестве V128 в соответствии с равенством:
EK1, …, K10(a) = X[K10]LSX[K9]…LSX[K2]LSX[K1](a),
где a∈V128.
Размер блока для шифра «Кузнечик» составляет 128 бит. После того, как соответствующий блок подан на вход для шифрования, его необходимо сложить по модулю два с первым раундовым подключом K1, затем выполнить девять раундов преобразований. Раунд включает три операции: табличная замена с помощью блока S, перемешивание информации с помощью преобразования L и сложение по модулю два с раундовым подключом K1+i, где i – номер соответствующего раунда. После 9 раундов преобразований блок открытого текста становится 128-битным блоком шифр-текста. Подробное описание шифра можно найти в работах [1, 3].
Чтобы определить дифференциальные свойства алгоритма «Кузнечик», достаточно определить дифференциальные свойства элементов, его составляющих. Шифр состоит из трех основных преобразований: S, L, X. Преобразование S аналогично замене байтов с использованием S-блока замены, преобразование L представляет собой сложную линейную операцию, основанную на перемножении полиномов в заданном поле, преобразование Х по сути представляет собой простую операцию сложения по модулю два данных. Дифференциальные свойства преобразования будем определять как вероятность изменения несходства двух входных слов при их прохождении через рассматриваемое преобразование. Под входным дифференциалом будем понимать разность, получаемую путём сложения по модулю два двух входных значений. Под выходным дифференциалом будем понимать разность, получаемую путём сложение по модулю два двух выходных значений.
Рассмотрим дифференциальные свойства для преобразования сложения данных с раундовым подключом. Так как данное преобразование представляет из себя по факту обычное сложение по модулю 2 двух входных значений с выходом в виде результата операции (в случае процесса шифрования/дешифрования рассматриваемого шифра данное преобразование обозначается как X и принимает на вход: значение для преобразования и один из подключей, который мы будем обозначать как «Дополнение»), то при рассмотрении его дифференциальных свойств возникает простое уравнение, определяющее выходной дифференциал (1) и, следовательно, дифференциальное свойство:
Вход1⊕Вход2 = ΔВход, Выход1⊕Выход2 = ΔВыход,
ΔВход⊕Дополнение1⊕Дополнение2 = = ΔВход⊕ΔДополнение = ΔВыход, (1)
где Входi при i = 1,2 обозначает входные слова, Выходi при i = 1,2 – выходные слова, а Дополнениеi при i = 1,2 – слова, поступающие в преобразование X вместе с соответствующим им входным словом.
Для большей ясности можно сказать, что дифференциальное свойство X преобразования заключается в том, что выходной дифференциал представляет из себя результат операции сложения по модулю 2 входного дифференциала и дополнительного, т.е. выходной и входной дифференциал равны при одинаковых дополнениях и не равны при разных дополнениях.
Рассмотрим дифференциальные свойства преобразования L. Несмотря на то, что преобразование L состоит из совокупности более простых преобразований, его всё равно можно рассматривать как элементарное. При определении дифференциальных свойств данного преобразования следует учитывать его свойства сложения по модулю два, т.е. следует учитывать независимость преобразования дифференциала двух входных слов через L преобразование от их компоновки. Данное свойство определяет дифференциальное свойство преобразования, и его можно выразить так, как представлено в формуле (2):
Вход1⊕Вход2 = ΔВход, Выход1⊕Выход2 = ΔВыход,
L(Вход1)⊕(Вход2) = L(Вход1⊕Вход2) = = L(ΔВход) = ΔВыход2, (2)
где Входi при i = 1,2 обозначает входные слова, Выходi при i = 1,2 – выходные слова.
Для большей ясности можно сказать, что дифференциальное свойство L преобразования заключается в том, что выходной дифференциал представляет из себя результат преобразования L над входным дифференциалом.
Рассмотрим дифференциальные свойства S преобразования. В алгоритме шифрования «Кузнечик» 128-битный блок преобразуемых данных разделяется на восемь 8-битных блоков, каждый из которых подвергаетсяпреобразованию. Преобразованиевыполняется в соответствии с установленной стандартом таблицей, заполнение которой можно найти в работе [3].
В общем случае алгоритм определения дифференциальных свойств любого блока замены можно выполнить в соответствии с алгоритмом, приведённым в работе [2].
Легко заметить, что существует только 256 возможных входных значений для одного π-преобразования и также существует только 256 значений дифференциалов для двух входных значений. Каждый дифференциал может быть образован одним из 256 способов. Для каждого такого случая необходимо определить значения на выходе π преобразования, сложив которые можно получить возможные значения дифференциалов на выходе.
Если рассмотреть более подробно значения выходных дифференциалов, то откроется замечательное дифференциальное свойство неравномерности распределения. Данное свойство подразумевает под собой соответствие конкретному входному дифференциалу некоторого количества выходных дифференциалов, которые повторяются и количеством не достигают числа 256. Следует обратить внимание на входной дифференциал, равный 0, так как он обладает свойством образовывать на входе и на выходе равные дифференциалы при любых парах входа (далее будем рассматривать получаемые результаты для него отдельно). В цифрах свойство неравномерности распределения обретает следующие размерности для алгоритма шифрования «Кузнечик»: при рассмотрении всех входных дифференциалов, можно увидеть, что для одного входного дифференциала минимальное количество уникальных выходных дифференциалов составляет 98 разных значений, максимальное – 114 разных значений из 256 возможных (здесь не учитывается входной дифференциал, равный нулю, т.к как он один приводит к единственному значению выходного дифференциала).
Кроме того, некоторые выходные дифференциалы повторяются несколько раз (все их повторения кратны двум из-за зеркального отображения пар текстов, образующих значение дифференциала). Так, минимальное повторение одного выходного дифференциала равно 0, а максимальное – 8.
Опираясь на рассмотренные дифференциальные свойства, рассмотрим возможность применения метода связанных ключей к анализу алгоритма шифрования «Кузнечик». Анализ с использованием связанных ключей относится к дифференциальному типу и был впервые предложен Эли Бихамом, Орром Данкеламном и Натаном Келлером [4–7]. Основной идеей метода является наличие нескольких взаимосвязанных ключей шифрования, связь которых определяется в соответствии с некоторой функцией F. Данная функция известна аналитику и выбирается им же.
При проведении анализа потребуется восстановить значения ключей. Пусть необходимо восстановить возможные 8-битные слова допреобразования, при этом известны некоторые случайные дифференциалы входа и выхода. В таком случае, чтобы восстановить возможные значения до преобразования, потребуется соотнести имеющийся входной дифференциал с количеством повторений выходного дифференциала и значениями конкретных выходов, его образующих. Выбирая значения из соответствующей позиции в паре, можно получить возможные значения до π преобразования. Представленное выше рассуждение можно применить и к восстановлению всего 128-битного слова до S преобразования, зная входной и выходной дифференциал. Для этого следует учесть, что преобразование S состоит из сочетания 16 π преобразований, а следовательно, S порождает композицию вероятностей восстановления в зависимости от вероятности.
Для проведения анализа будем считать, что аналитик выбирает два дифференциала для двух пар ключей и соответствующих им подключей. В обоих случаях один из ключей будет общим, он и будет восстанавливаться. Дифференциалы ключей имеют следующее зависимости:
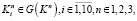
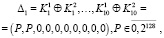
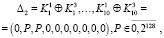
где G обозначает процесс генерации подключей, Kn – мастер ключ с номером n и 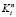 – подключ ключа n с номером i. Следует учесть, что непосредственно сам Р дифференциал должен в каждом 8-битном блоке иметь ненулевое значение, это нужно для успешного восстановления ключей. Ненулевые компоненты Р необходимы для вариативного прохождения S преобразования, иными словами, они нужны для создания вариантов пар до и после S преобразования в меньшем количестве, чем все возможные. Далее будем называть мастер-ключ шифрования ключом или мастер-ключом, а все подключи (в том числе и части разбитого мастер-ключа) соответственно подключами.
– подключ ключа n с номером i. Следует учесть, что непосредственно сам Р дифференциал должен в каждом 8-битном блоке иметь ненулевое значение, это нужно для успешного восстановления ключей. Ненулевые компоненты Р необходимы для вариативного прохождения S преобразования, иными словами, они нужны для создания вариантов пар до и после S преобразования в меньшем количестве, чем все возможные. Далее будем называть мастер-ключ шифрования ключом или мастер-ключом, а все подключи (в том числе и части разбитого мастер-ключа) соответственно подключами.
Описанные выше взаимосвязи подключей невозможны при использовании аналитиком оригинальной функции выработки подключей, но такая связь не противоречит теории анализа методом связанных ключей, т.к. искомый ключ соответствует функции выработки подключей шифра «Кузнечик».
Также будем считать, что аналитик может шифровать и расшифровывать любые тексты, не зная значения ключей, но зная, какой из двух ключей применяется в конкретном случае шифрования/дешифрования. Тогда для успешной проверки надёжности необходимо будет выполнить два основных этапа.
На первом этапе (рисунок) восстановления ключа необходимо использовать пару ключей с дифференциалом Δ1. Далее будем считать ключ K1 первым и общим для двух дифференциалов.
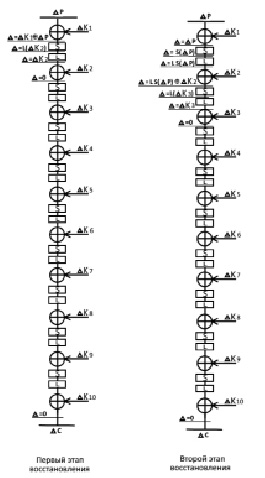
Общий процесс атаки на полный шифр «Кузнечик»
В первую очередь следует подобрать такую пару закрытых текстов, чтобы она давала дифференциал, равный нулю, то есть, таким образом, отбеливаются все дифференциалы, расположенные ниже сложения по модулю два со вторыми подключами. Вероятность отбеливания всегда равна 1 при заявленных ранее дифференциах ключей, ведь S и L преобразования (и обратные им) для равных входных значений возвращают равные выходные значения. После нахождения нужных закрытых текстов можно получить пару открытых текстов, дифференциал которых можно подсчитать, зная сами значения пары текстов. Далее требуется вычислить дифференциал после сложения по модулю два с первыми подключами, что не представляет сложности.
В результате имеются значения дифференциалов до и после первого S преобразования. Полученные результаты дифференциалов необходимо разделить на слова по 8 бит и дальше отдельно работать с каждым словом. В результате будут найдены возможные комбинации значений входных пар, соответствующие условию входного дифференциала, которые на выходе будут образовывать из выходных значений выходной дифференциал. Так как имеется только одна пара известных дифференциалов до и после S преобразования, то комбинаций возможных пар будет достаточно мало.
При хорошем выборе дифференциала для первого подключа, закрытых текстов и второго подключа можно получить в среднем V1 возможных пар значений до первого S преобразования. Зная открытые тексты и значение перед первым S преобразованием, можно восстановить V1 первых подключей K1 и K2. Когда станут известны возможные пары первых подключей, автоматически станут известны V1 возможных и соответствующих K1 первых подключей K3, что является целью первого этапа восстановления. В конце данного этапа создаётся V1 пар первых подключей ключа K1 и K3 с учётом их связи в дифференциале Δ2.
Для второго этапа (рисунок) восстановления ключа нужно использовать дифференциал ключей Δ2.
После того, как вычислены возможные значения первых подключей для первого и третьего ключа, используя неизвестные ключи K1 и K3, необходимо выбрать пару закрытых текстов в соответствии с первым этапом восстановления. Однако в данном случае нулевой дифференциал будет образован, начиная с выхода операции сложения по модулю два для третьего раунда (в соответствии с использованием дифференциала ключей Δ2). Так как известны все потенциальные первые подключи ключа K1 и K3, то можно при единственной вычисленной паре открытых текстов вычислить все возможные значения до X преобразования со вторыми подключами.
Когда вышеперечисленные действия выполнены, можно по аналогии с первым этапом восстановить значения возможных пар текстов до второго S преобразования для каждой пары первых подключей K1 и K3. То есть получить значения до и после сложения по модулю два со вторым подключом для каждой возможной пары первых подключей K1 и K3, и можно посчитать возможные вторые подключи в количестве V2. В результате комбинации полученных первых и вторых (V1 и V2) подключей можно получить их общее количество. Перебор всех возможных комбинаций первых и вторых подключей первого ключа и генерации из них всех остальных порождает списки подключей, соответствующих перебираемой паре первых и вторых подключей. Проверка всех возможных выработанных подключей на анализируемом алгоритме шифрования и сравнение результатов шифрования анализируемого алгоритма с результатами шифрования проверяемого на практике шифра позволит найти искомое значение ключей.
Для большей ясности можно сказать, что результатом данной работы является создание теоретической базы проверки надёжности шифра «Кузнечик». При этом показана невозможность заявленной взаимосвязи ключей, но в то же время показано соответствие сути метода проверки (сам метод связанных ключей и правила выработки искомого ключа) всем правилам алгоритма шифрования.
Следует отметить, что рассмотренный метод анализа с использованием связанных ключей маловероятен при практическом применении и зачастую может существовать лишь из-за ошибки протоколов безопасности или сбоев программ безопасности, следовательно, практической ценности не имеет почти полностью, однако очень полезен для изучения криптографических свойств шифров.
Работа выполнена при поддержке гранта РФФИ № 15-37-20007-мол-а-вед.



