При эксплуатации опасных производственных объектов (ОПО) во многих случаях в их состав могут входить особые виды технических устройств (ТУ), эксплуатация которых сопряжена с повышенным риском причинения этими устройствами ущерба человеку, окружающей среде, а также другой технике [3].
К их числу могут быть отнесены различные подъемные сооружения, а также сосуды, работающие под избыточным давлением.
Повышенная опасность таких ТУ связана с хранением в них, переработкой или перемещением этими устройствами различных веществ, содержащих значительные запасы энергии. При определенных неблагоприятных обстоятельствах эта энергия может выйти из-под контроля и привести к авариям, несчастным случаям или катастрофам.
В связи с этим к безопасности эксплуатации применяемых на ОПО технических устройств и, в частности, к такому её этапу, как продление ресурса, предъявляются особые, повышенные требования [4].
Цель исследования
Одной из задач, связанных с обеспечением безопасности эксплуатации оборудования ОПО, является разработка методов оценивания и прогнозирования технического состояния входящих в их состав ТУ на продлеваемом периоде эксплуатации.
Материалы и методы исследования
За время жизненного цикла технического устройства в его конструкции происходит накопление повреждений, которое неизбежно ведет к его списанию или отказу. Процесс накопления повреждений включает в себя обширный ряд явлений, таких как коррозия, эрозия, износ, ползучесть, выносливость, рост усталостных трещин, старение полимеров, гниение, электролиз и т.п. Некоторые из этих явлений вызываются химическими реакциями, другие – механическими воздействиями, а некоторые и тем и другим.
Разрушение твердых тел под действием эксплуатационных нагрузок происходит не мгновенно при достижении напряжением предельных значений, а представляет собой относительно длительный процесс зарождения и развития несплошностей в теле, связанный с преодолением значительных энергетических барьеров.
Экспериментальные исследования и теоретические построения возможных механизмов развития несплошностей показали сложность и многообразие форм протекания процесса разрушения. Несмотря на это, возникшее относительно давно деление процесса разрушения на три стадии не претерпело серьёзных изменений. К ним можно отнести стадии нарушения сплошности и возникновения субмикро- и микротрещин, размер которых меньше типичного размера структуры материала (диаметра зерен, расстояния между включениями и т. п.); стадию пересечения отдельными микротрещинами границ зерен и перерастания в макротрещины. Эта стадия заканчивается, когда трещина достигает критического размера после чего происходит разрушение материала.
Накопление и развитие повреждений является результатом действия эксплуатационных нагрузок – энергетического воздействия. Оно проявляется через изменение геометрических параметров повреждений.
Соответственно, для оценивания и прогнозирования технического состояния ТУ могут быть предложены два критерия:
Первый основан на сравнении с допустимым значением показателя энергетической характеристики процесса развития повреждений.
Второй основан на сравнении с допустимым значением показателя, характеризующего геометрические параметры повреждений.
Теоретическими основами построения модели, основанной на применении первого – энергетического критерия, является теория повреждаемости технических устройств с циклическим характером работы [5].
Согласно этой теории повреждаемость ТУ или изменение его технического состояния характеризуется функцией повреждаемости. Считается, что условием достижения циклически нагруженных элементов (ЦНЭ) предельного состояния является равенство произведённой работы значению внутренней работы, необходимой для разрушения ТУ при статической нагрузке, при этом его ресурс в циклах нагружения равен
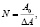
а функция повреждаемости
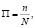
где А0 – работа, необходимая для нарушения сплошности материала статической нагрузкой и определяемой из диаграммы нагружения;
ΔА – внутренняя работа, совершаемая за один цикл нагружения;
N – ресурс элемента в циклах нагружения;
n – число циклов нагружения при эксплуатации.
Условие того, что ЦНЭ в эксплуатации не достигнет предельного состояния, описывается отношением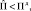 
где 
– случайное значение функции повреждаемости, а Пд – допустимое значение функции повреждаемости. В связи с этим, мера возможности наступления предельного состояния может быть охарактеризована следующим выражением:
,
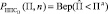где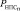 
– вероятность недостижения предельного состояния по параметру значения функции повреждаемости;
n – текущая наработка ТУ в циклах.
Выбор и обоснование закона распределения функции повреждаемости, а также и его числовых характеристик достаточно подробно изложен в работе [5].
Исходными данными для расчета характеристик технического состояния и прогнозирования его изменения для ЦНЭ являются данные о режимах их работы и данные о физико-механических свойствах материала конструкции. Режимы работы ЦНЭ определяются статистическими характеристиками числа циклов нагружения за некоторый промежуток времени (математическим ожиданием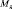 
и дисперсией 
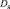) и статистическими характеристиками нагрузок за этот же период времен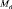и 
и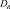 
. Используя эти данные, нетрудно рассчитать характеристики технического состояния в виде вероятности недостижения ЦНЭ предельного состояния или наработки, в течение которой они могут эксплуатироваться с требуемым уровнем надёжности и безопасности.
Формализуя процесс накопления повреждений с точки зрения оценивания их геометрических параметров, необходимо отметить, что в соответствии с теорией разрушения существуют следующие варианты образования трещин:
1) развитие трещины от максимально возможного дефекта технологической природы, допускаемого нормативно-технической документацией;
2) развитие трещины от дефекта технологической природы, пропущенного в эксплуатацию из-за несовершенства средств дефектоскопии и существенно превышающего нормы дефектов для изготовления и эксплуатации;
3) развитие трещины, зародившейся в эксплуатации в результате недостатков конструирования или эксплуатации.
При наличии в конструкции трещины или объемного дефекта технологической природы (непровар, несплавление и т.п.) эти дефекты представляются как трещины. Обусловлено это тем, что трещина является самым опасным дефектом сплошности материала, и такой подход автоматически обеспечивает консервативность анализа. Кроме того, объемные и плоские дефекты сплошности могут иметь на своих краях острые микронадрывы, микротрещины, что приближает их поведение к поведению трещин.
Как уже было отмечено, постепенный рост трещины в условиях реальной эксплуатации может окончиться достижением трещиной критических размеров, после чего трещина переходит в стадию быстрого неустойчивого развития, которая может вызвать окончательное разрушение конструкции. Следовательно, существует некий критический размер трещины l*, при достижении которого происходит разрушение конструкции, или, другими словами, металлоконструкция переходит в предельное состояние.
При прогнозировании технического состояния ТУ, необходимо оценить меру объективной возможности наступления предельного состояния. В качестве такой меры можно выбрать вероятность ненаступления предельного состояния. Параметром распределения в данном случае является размер трещины
,
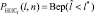где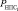 
– вероятность ненаступления предельного состояния по параметру l;
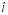– случайная величина размера трещины;
n – текущая наработка ТУ.
Имеющаяся в настоящее время приборная база контроля качества конструкционных материалов позволяет обнаруживать трещины (и отнесенные к ним дефекты) в широком диапазоне их размеров. При этом минимальные обнаруживаемые дефекты имеют размеры на порядок ниже критических размеров трещины и, таким образом, не являются браковочными при оценивании текущего технического состояния ТУ. Однако объективно существующие процессы разрушения, обусловленные наличием концентраторов напряжений в виде трещин, требуют проведения исследований и прогнозирования их развития во времени.
Проведенные ранее исследования [1], свидетельствуют о том, что распределение случайных эффективных размеров дефектов, обнаруживаемых в ходе проведения дефектоскопии ТУ с применением ультразвуковых средств, удовлетворительно описывается нормальным законом
,
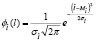числовые характеристики которого могут быть определены из статистики.
Вполне обоснованно можно предположить, что дефекты не являющиеся в момент текущего контроля, соответствующего наработке n, браковочными или критическими (по своим размерам), с увеличением наработки могут достичь предельного состояния. При этом, учитывая нормальность распределения размеров трещин, к определенной наработке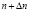 
критического размера достигнет только часть дефектов с размерами, принадлежащими интервалу [ln–, ln+]. Вероятность этого события определится как
,
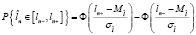где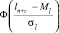 
– табулированная функция Лапласа;
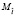– математическое ожидание характерного размера (длинны) трещины;
– среднее квадратическое отклонение характерного размера (длинны) трещины.
По физическому смыслу вероятность попадания в момент, соответствующий наработке n, размера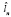 
в интервал [ln–, ln+] соответствует вероятности достижения или недостижения предельного состояния к наработке n + Δn, т.е.
.
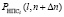
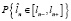Для оценивания границ интервала [ln– , ln+ ] необходимо формализовать и оценить скорость роста размера трещины в конкретных эксплуатационных условиях.
Опишем закономерности роста усталостных трещин в терминах механики хрупкого разрушения [2]. Пусть процесс нагружения σ(t) – циклический, т.е. состоит из последовательности реализаций, многократно пересекающих некоторый средний (вообще, переменный) уровень напряжений. Для упрощения примем, что каждый цикл – отрезок реализации между двумя соседними положительными пересечениями среднего уровня – содержит по одному максимуму σmax и одному минимуму σmin. Если пренебречь влиянием частоты нагружения и считать температуру и другие условия окружающей среды постоянными, приращение размера трещины Δl за один цикл должно зависеть только от l, σmax и σmin. В рамках механики хрупкого разрушения число определяющих параметров сокращается до двух: ими служат максимальное и минимальное за цикл значения коэффициента интенсивности напряжений. Считая приращение Δl малым, общее число циклов весьма большим, размер трещины l – непрерывно дифференцируемой функцией непрерывного аргумента – числа циклов n, получим уравнение относительно скорости роста усталостной трещины
,
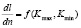где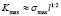 
, 
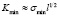– минимальный и максимальный коэффициенты интенсивности напряжений.
Детальный обзор эмпирических уравнений для скорости роста трещин дан в работе [2]. В настоящее время в прикладных расчетах широко применяют уравнение Формана
,
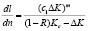где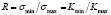 
коэффициент асимметрии цикла;
Kc – критическое значение коэффициента интенсивности напряжений, при котором наличие трещины в материале может привести к разрушению конструкции.
Правая часть выражена через размах коэффициента интенсивности напряжений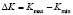 
в пределах цикла. Для большинства конструкционных металлов и сплавов принимают т = 2...6 (для углеродистых сталей при не слишком высоких напряжениях m ≈ 4). При т = 4 обычно принимают с = 10-16... 10-12 мм7Н-4.
Результаты исследования и их обсуждение
Исследовав механизм и динамику развития трещин, оценивание диапазона размеров трещин, которые могут достичь предельного состояния к заданной наработке nnp, может быть сведено к анализу следующих зависимостей:
;
,
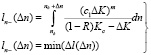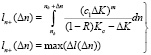где Δn – интервал прогнозирования;
nm – количество циклов, соответствующее текущей наработке или соответствующее достижению трещиной критических размеров;
Δl(Δn) – диапазон размеров дефектов, которые на интервале прогнозирования превысят критическое значение;
min(Δl(Δn)) – минимальное значение размера дефекта из диапазона размеров дефектов, которые на интервале прогнозирования превысят критическое значение;
max(Δl(Δn)) – максимальное значение размера дефекта из диапазона размеров дефектов, которые на интервале прогнозирования превысят критическое значение.
После оценивания границ интервала [l n– , l n+ ] имеется возможность прогнозирования значения вероятности недостижения предельного состояния к каждому конкретному циклу.
Выводы
Таким образом, обосновав вид двух показателей, характеризующих процесс развития повреждений с точки зрения его энергетики и с точки зрения динамики его геометрических параметров, предлагаемый двухкритериальный подход к оцениванию и прогнозированию технического состояния может быть формализован следующим образом:
,
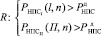где R – событие, заключающееся в том, что ТУ предельного состояния не достигло;
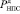– допустимое значение вероятности ненаступления предельного состояния.