Для литья под давлением (инжекционного литья) полимерных композиционных материалов (ПКМ), армированных дискретным высокомодульным волокном, характерно то, что распределение волокна (его направленность и длина) в готовом изделии будет значительно варьироваться. Для моделирования данного процесса можно использовать математические и компьютерные модели [1–6]. Таким образом, заданные условия процесса литья влияют на конечные механические свойства детали [8–11]. При этом композитный материал является анизотропным и гетерогенным, что сильно осложняет проведение достоверной симуляции классическим подходом, основанным на макроскопической модели. Прогнозирование свойств такого материала возможно посредством мультимасштабного подхода [7, 13].
Гетерогенное твёрдое тело состоит из фазы материала-матрицы и множества фаз-включений (например, волокон, микрополостей, частиц или микротрещин). Можно выделить 2 уровня: микроскопический и макроскопический. Гетерогенность структуры проявляется на микроуровне, в то время как на макроуровне твёрдое тело можно рассматривать как локально гомогенное.
Классическая схема перехода от микромасштабной к макромасштабной модели заключается в следующем.
1. Экспериментально де факто либо теоретически численными методами определяются ключевые параметры микроструктуры. Для коротковолокнистых ПКМ – это распределение и направленность армирующего волокна в полимерной матрице. Длина волокна известна априори.
2. На основе параметров микроструктуры (микромодель структуры материала) с применением методов гомогенизации механики сплошных сред рассчитывают анизотропные механические свойства материала в элементарном макрообъеме (макромодель структуры материала).
3. С использованием макромодели, когда в любой точке материала рассчитаны его анизотропные механические свойства, производят необходимый прочностный анализ в зависимости от граничных и начальных условий.
На практике численными методами невозможно получить механические свойства на уровне достаточно малого масштаба. Поэтому берут в рассмотрение макроуровень и считают, что каждая материальная точка является центром ячейки представительского объёма (ЯПО) с соответствующей гетерогенной микроструктурой. Классическая механика твёрдых тел применяется для макромасштаба, при этом в каждой расчётной точке значения напряжений и деформаций является граничным условием (ГУ) соответствующей ЯПО. Решением каждой ЯПО являются значения напряжений и жёсткости, которые действуют на макроуровне.
Для ЯПО с классическими граничными условиями макронапряжения и деформации равны среднеобъёмным ЯПО неизвестных полей микронапряжений и деформаций внутри ЯПО. Согласно теории линейной эластичности, соотнесение двух средних значений даёт эффективные и общие жёсткости композита на макроуровне.
Для решения проблемы ЯПО, можно использовать конечно-элементный (КЭ) метод. Несмотря на то что метод является очень распространённым и точным, создание достаточно реалистичной сетки микроструктуры является сложной задачей. Кроме того, при нелинейной постановке задачи (например, неэластичное поведение материала) возникают большие процессорные времязатраты.
Совершенно другой подход предлагает метод гомогенизации по среднему полю (ГСП), который основан на предположении о взаимосвязях средних полей напряжений и деформаций в каждой фазе ЯПО (рис. 1). По сравнению с прямым КЭ-методом и другими существующими методами перехода между макро- и микроуровнями, ГСП является самым простым в использовании и наиболее быстрым. Тем не менее, его недостатком является невозможность предоставить детальную информацию о полях напряжений и деформаций в каждой фазе, и он применим только для эллипсоидной формы включений.
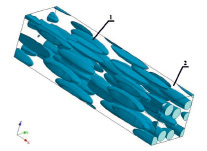
Рис. 1. Ячейка представительского объёма композиционного материала: фаза-включение (1), фаза материала-матрицы (2)
Тензор ориентации второго порядка (aij) является эффективным способом описания ориентации волокна при инжекционном литье. Тензор состоит из девяти компонент с индексами, обозначающими направление потока, поперечное направление и направление вдоль толщины детали. Вследствие свойства симметричности aij = aji и условия нормализации (a11 + a22 + a33 = 1) девять компонент сокращаются до 5 независимых переменных:
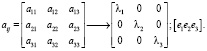
Наибольший интерес представляют следующие три компоненты:
a11 – ориентация волокна в направлении течения (значение изменяется от 0 до 1);
a22 – ориентация волокна в поперечном потоку направлении (0…1);
a13 – угол наклона в плоскости 1–3 (– 0,5…0,5).
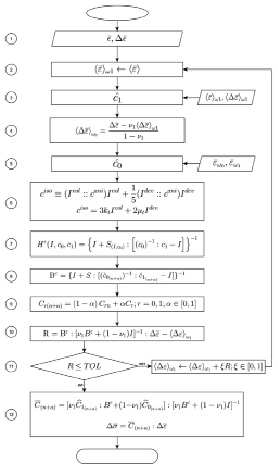
Рис. 2. Схема алгоритма метода среднего поля
Одним из получивших распространение в системах численного моделирования алгоритмов гомогенизации свойств материала является метод эффективного поля [1]. Схема алгоритма представлена на рис. 2.
1. На временном интервале [tn, tn+1] исходными данными являются общие деформации на макроуровне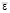 
и приращения деформации 
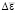, а также значения остальных параметров к моменту времени tn.
2. Начало расчёта приращения усреднённой деформации в фазе включения.
3–5. Определение матрицы расчётных коэффициентов жёсткости материала включений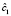 
и материала матрицы 
.
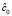6. Расчёт усреднённой деформации в матрице.
7. Выделение изотропной части матрицы жёсткости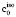 
.
8. Вычисление тензора Эшелби S(I,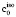 
) для единичного включения матрицы модулей жёсткости.
9. Вычисление значений дискретных расчетных модулей жесткости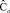 
и 
на временном шаге tn+α:
а) 
б)
Рис. 3. Исходная сетка инжекционного литья (а) и структурная сетка прочностного расчёта (б)
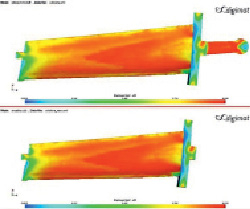
Рис. 4. Результат процедуры маппинга
10. Вычисление тензора концентраций деформаций.
11. Проверка сходимости расчётной и исходной (для шага tn+α) усреднённой деформаций во включении. Если |R| в пределах допуска на усреднённую деформацию в фазе наполнителя, то выходим из цикла. Иначе осуществляется новая итерация (переход на первый шаг) с уменьшенным значением 
.
12. После завершения цикла вычисляются значения макроскопических матриц жёсткости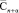 
и тензора напряжений 
.
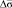Рассмотренный алгоритм был апробирован при численном моделировании формирования структуры ПКМ и расчета прочности литой лопатки из ПКМ в связке CAE-систем Moldex3D-Digimat-ANSYS.
Объект моделирования – статорная лопатка компрессора ГТД. Полимерный композиционный материал – полиэфиэфиркетон, на 40 % армированный углеволокном (PEEK90HMF40).
Современные CAE-системы моделирования процесса литья могут предложить параметры процесса лишь исходя из рекомендуемых параметров переработки материала. При этом выбор оптимальных параметров остаётся за технологом, и такая оптимизация параметров должна проводиться посредством соответствующих методов, в том числе встроенных в CAE-систему (например, метод Тагути). Однако для верификации конкретной численной модели требуется проведение её калибровки для устранения ошибки при расхождении граничных условий моделирования и реальных параметров технологического процесса, т.к. модель всегда является упрощением. В частности, можно контролировать теоретический и экспериментальный профили течения и оценивать разницу между ними.
Как уже было отмечено выше, для определения прочностных характеристик неоднородного материала необходимо определение направления и распределения волокон [5, 6], являющихся исходными данными вышеизложенного алгоритма гомогенизации. Эти параметры описываются тензором ориентации второго порядка. Для их графического представления генерируется собственный вектор. Собственный вектор показывает главные направления ориентации волокна, и собственные значения дают статистическое распределение волокна в направлении главных осей (от 0 до 1). Исходя из этих данных, определяется направленность эллипсоида, которая полностью описывает распределение волокна по направлениям для каждого конечного элемента.
Объёмное распределение и направленность волокон в форме тензора ориентации есть результат моделирования инжекционного литья в CAE-системе. При этом КЭ-сетка, используемая в расчёте в Moldex3D, не обязательно будет совпадать с сеткой ANSYS, поскольку алгоритмы прочностного анализа отличаются от алгоритмов моделирования течения расплава (рис. 3). Поэтому необходимо провести перенос тензоров ориентации между сетками (маппинг), что осуществляется с помощью DIGIMAT-MAP (рис. 4).
Рассмотренный алгоритм гомогенизации является эффективным средством для перехода от параметров микроструктуры к макросвойствам материала с целью учёта его локальной анизотропии при проектировании изделий и оптимизации технологических режимов инжекционного литья.