Городской округ – г. Камышин Волгоградской обл., население 110 тыс. человек, количество маршрутов городского общественного автотранспорта 19, из которых 12 являются наиболее напряженными по пассажиропотоку. Руководство города, считая целесообразным пересмотр структуры управления автотранспортом, привлекло группу сотрудников Камышинского технологического института (филиал) ФГБОУ ВО Волгоградского технического университета для выработки подходов к решению следующего ключевого вопроса: какова должна быть степень участия муниципалитета в управлении не только муниципальным, но и частным пассажирским автотранспортом?
Обязательным условием заказчика было проведение натурного обследования пассажиропотока города, методика проведения которого и анализ представлены в работах [1–7]. При решении поставленной задачи требования к критериям оптимизации определяются необходимостью найти такое решение по предмету оптимизации, чтобы обеспечить компромисс между частично несовпадающими интересами различных социальных групп горожан. Эта задача затрагивает интересы пассажиров, владельцев частных транспортных средств, муниципальных властей, управления дорожным движением.
Общепринятый подход состоит в привлечении экспертов, которым предоставляется имитационная модель транспортных потоков. Но из-за неизбежного влияния различий в стиле принятия решений каждого эксперта желательно поддержать работу экспертной группы оценками показателей решений, не зависящих от индивидуальной стратегии. Потребность в выработке таких решений, зависящих только от объективных внешних факторов и выбранных критериев, особенно актуальна при решении новых задач, по которым у группы экспертов недостаточно надежна база знаний (именно к такому случаю относится рассматриваемая задача).
Для решения поставленной задачи использован известный подход к объективизации процесса принятия решений, основанный на применении оптимизационных моделей. Полученные оптимальные результаты представляются экспертам для принятия окончательного решения [9]. Данный подход позволяет представить экспертам граничные значения расчетных показателей, соответствующие предельному использованию всех ресурсов системы ограничений для достижения экстремума выбранного критерия. Естественно, окончательные решения, принимаемые экспертами, окажутся более «щадящими», учитывающими как объективную неточность исходных данных, так и наличие групп интересов, не учтенных в критерии оптимизации. Но польза в количественных оценках показателей, потенциально достижимых на множестве ограничений, несомненна. Дополнительным аргументом в пользу выбора оптимизационного подхода является возможность исследования зависимостей критерия и технико-экономических показателей от параметров системы ограничений. Например, в рассматриваемой задаче такие параметры относятся к варьированию степени участия муниципалитета в управлении частным автотранспортом.
Схема использования оптимизационного подхода:
1. Исходя из особенностей конкретной задачи, выработать систему критериев принятия решений.
2. Обосновать способ перехода от многокритериальной задачи к задачам оптимизации единственного критерия.
3. Сформировать систему ограничений, определяющих допустимую область изменения рассчитываемых показателей, а также косвенно учитывающих требования к остальным критериям, не принятым в качестве оптимизируемого.
4. Выбрать алгоритм и программную среду для решения оптимизационной задачи.
5. Провести расчеты при варьируемых параметрах критерия и системы ограничений.
Эта схема универсальна и известна, но попытки ее использования на практике нечасты из-за трудностей, связанных с высокой размерностью, недостаточностью исходных данных и несоответствием реальной сложности задачи существующему алгоритмическому обеспечению. Поэтому примеры успешной «привязки» схемы к задачам, сформулированным заказчиком лишь на содержательном уровне, содержат элементы новизны, состоящие как в выборе подхода к решению, так и в создании модели, которая, с одной стороны, отвечает практической постановке задачи и, с другой стороны, может быть решена при существующем уровне развития теории оптимизации. Такие примеры (в их числе и рассматриваемый нами) можно рассматривать с позиции усиления практичности теории оптимизации.
Предмет оптимизации состоит в следующем:
1. Получить оценку количества частных транспортных средств (ТС) на каждом маршруте.
2. Рассчитать размер ожидаемой платы за проезд на каждом маршруте.
3. Оценить величину прибыли на каждом маршруте для прогноза размера налоговых поступлений от владельцев каждого маршрута.
Формальное описание и решение задачи
Решение задачи может оказаться различным в зависимости от того, какая из заинтересованных социальных групп будет оценивать качество системы транспортного обслуживания и предложит главный показатель, отвечающий ее интересам. Соответственно был разработан перечень следующих показателей качества как функции искомых переменных S:
1. Показатель Q1(S): суммарная часовая прибыль от эксплуатации ТС всех маршрутов (отвечает интересам муниципалитета и города в целом, поскольку обеспечивает высокий уровень налоговых поступлений в городской бюджет):
,
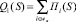Пi(S) – прибыль от эксплуатации i-го маршрута, i∈wa.
2. Показатель Q2 (S): удельная часовая прибыль всех частных транспортных организаций в расчете на 1 ТС/час (отвечает интересам владельцев частных транспортных средств):
,
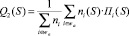ni(S) – количество транспортных средств, обслуживающих i-й маршрут, i∈wa.
3. Показатель Q3(S): значение суммарного (по всем маршрутам) количества ТС/час (отвечает интересам управления дорожным движением):
.
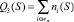4. Показатель Q4(S): средневзвешенная (по числу ТС/час на маршрутах) плата за проезд (отвечает интересам пассажиров):
,
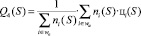цi(S) – стоимость проезда, которую устанавливает владелец на i-го маршрута, i∈wa.
5. Показатель Q5(S): минимальное значение максимальной (по всем маршрутам) платы за проезд (вариант отвечает интересам владельцев маршрута, поскольку направлен на смягчение конкуренции между маршрутами):
.
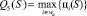Соответственно задача определения значений S искомых переменных, отвечающих компромиссу между частично противоречивыми интересами различных социальных групп, формулируется как задача оптимизации вектора показателей Q(S):
{Q(S) = [Q1 (S),… Q5 (S)]T}.
Подход, предложенный для решения задачи векторной оптимизации, содержит 2 этапа. На этапе 1 решается 5 однокритериальных задач, в каждой l-й из которых l = 1,…,5, рассчитываются оптимальные значения искомых переменных S* и соответствующее им оптимальное значение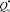 
(S*) соответствующего показателя Qv(S), выбираемого в качестве критерия. Значения остальных показателей Qm, m = 1,…,5, m ≠ v, будут в общем случае иметь значения, не только отличающиеся от оптимальных, но и (возможно) окажутся неприемлемыми для других социальных групп. Критерии Q1(S), Q2(S) подлежат максимизации, остальные критерии – минимизации.
На этапе 2 решается задача нахождения компромиссного решения с использованием двух подходов. Первый базируется на скаляризации вектора Q(S), которая проводится одним из следующих способов:
– нахождение решения, доставляющего минимум средневзвешенному значению нормированных отклонений показателей от их оптимальных значений:
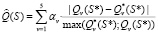. (1)
Веса av каждого из компонентов рассчитываются исходя из численности горожан, заинтересованных в соответствующем критерии;
– использование принципа чебышёвского выравнивания, при котором минимизируется единая граница z нормированных отклонений показателей от оптимальных значений:
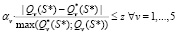. (2)
Расчеты для компромиссных критериев (1), (2) должны быть выполнены как для различных, так и для равных значений весовых коэффициентов av. Поскольку показатели Qv, v = 1,…,5 не полностью противоречат друг другу, можно было ожидать, что решения не будут сильно зависеть от выбора весов av, что и подтвердилось в расчетах.
Второй подход состоит в оптимизации показателя Q1(S), а для учета интересов отдельных групп горожан предусматриваются различные способы участия муниципалитета в управлении частными транспортными организациями.
В статье [8] представлена формализованная модель статической оптимизации структуры пассажирского транспорта небольшого города. В данной работе описаны примеры использования разработанных математических моделей для повышения эффективности транспортной системы г. Камышина, имеющего 19 маршрутов и 78 остановок. Характеристика масштаба оптимизационных задач: число искомых переменных 200, число ограничений-равенств 100, число ограничений-неравенств 400.
Результаты исследования и их обсуждение
В таблице приведены результаты решения частных оптимизационных задач с критериями во всех вариантах 1...5 на системе ограничений блока 1 (как отмечалось выше, эти ограничения соответствуют почти рыночному варианту работы частной транспортной системы).
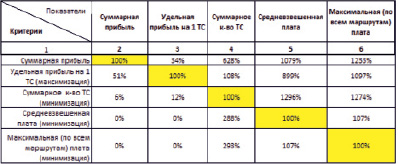
Результаты оптимизации частных критериев
В таблице за 100 % принято оптимальное значение каждого из частных критериев, перечисленных в столбце 1; остальные показатели в строке, соответствующей оптимизации частного критерия, рассчитаны в процентах экстремума, который был бы достигнут при выборе каждого из этих показателей в качестве критерия. Хотя расчеты оказываются полезными для прогноза тенденций, которые порождает принятие каждого из частных критериев, нужно отметить, что все варианты, показанные в таблице, являются неприемлемыми.
1. Ориентация на максимальную сумму налоговых поступлений (критерий Q1(S)) приводит к резкой дифференциации маршрутов по значению прибыли. Суммарное количество ТС/час превзойдет на 20 % существующее значение, которое эксперты считают завышенным. Средневзвешенная плата за проезд более чем в 2 раза превысит существующую с разбросом значений от 0,5 до 3,8 значений действующей платы. Данный вариант не может устроить ни частные транспортные организации, ни управление дорожным движением, ни пассажиров.
2. Ориентация на учет интересов владельцев частных транспортных средств (критерий Q2(S)) может привести к резкому сокращению количества ТС/час до минимально допустимого. На 80 % маршрутов количество ТС окажется на уровне минимально допустимого, и лишь на маршрутах с напряженным пассажиропотоком на концевых участках количество ТС/час будет незначительно больше минимально допустимого. Средневзвешенная плата за проезд превысит существующую в 2,5 раза с разбросом значений от 0,8 до 3,4 значений действующей платы. Суммарная прибыль частных транспортных организаций сократится в 2 раза по сравнению с вариантом 1; 20 % маршрутов окажутся бесприбыльными. Данный вариант противоречит интересам пассажиров и муниципалитета как выразителя интересов горожан в целом.
3. Ориентация на учет интересов управления дорожным движением (критерий Q3(S)) приведет к сокращению количества ТС/час на всех участках до допустимого минимального значения. Поэтому можно ожидать, что возрастет как время ожидания пассажиров на остановках, так и плата за проезд (в среднем в 3,7 раза при незначительном разбросе между маршрутами). 50 % маршрутов окажутся бесприбыльными; общая прибыль транспортных организаций может сократиться до 6 % значения по варианту 1. Данный вариант противоречит интересам частных транспортных организаций и города в целом.
4. Ориентация на учет интересов пассажиров (критерий Q4(S)) приведет к тому, что частная транспортная система станет бесприбыльной. Компенсация затрат частной транспортной системы может быть обеспечена при средневзвешенной плате за проезд в размере 30 % существующей при разбросе от 27 % до 34 % существующей платы за проезд. Этот вариант, привлекательный не только для пассажиров, но и для управления дорожным движением, не может быть реализован, т.к. противоречит принципам частного предпринимательства.
5. Ориентация на выравнивание платы за проезд (критерий Q5(S)) приводит к тем же последствиям, что и предыдущий вариант, с небольшим сокращением разброса платы: от 29 % до 31 % существующей платы.
Приведенный анализ показал, что в рамках двухуровневой структуры управления частным общественным автотранспортом не удастся обеспечить компромисс между интересами различных социальных групп, заинтересованных в работе транспортной системы. Результаты оптимизации по вариантам скаляризации векторного критерия приведены в отдельной статье.
Работа выполнена при финансовой поддержке РФФИ, проект 15-47-02321.