В настоящее время сфера применения криптографических методов защиты информации постоянно увеличивается. Это связано с тем, что системы шифрования играют важную роль в сохранении и передаче конфиденциальных данных. Симметричные алгоритмы по сравнению с асимметричными алгоритмами шифрования обладают целым рядом достоинств, таких как более простая аппаратная и программная реализации, а также высокая скорость зашифрования и расшифрования [1]. Среди симметричных шифров особое место занимают SPN-шифры, в которых используют подстановочно-перестановочную сеть. Однако в процессе работы шифраторы SPN-шифров могут быть подвергнуты атакам типа сбоев. Это приводит к нарушению работы шифратора и снижению степени защиты данных. Поэтому разработка алгоритмов, позволяющих устранить эти последствия, является актуальной задачей.
Цель исследования
В настоящее время для повышения надежности работы SPN-шифр-систем предлагается использовать дублирование, маскирование ошибок методом «2 из 3», а также использовать многократный просчет. Однако данные методы устранения последствий сбоев в работе шифратора характеризуются значительными схемными затратами. Это связано с тем, что они не в полной степени используют математическую основу SPN-шифров, реализованных в полях GF(28). В качестве перспективного направления решения данной проблемы можно отметить использование корректирующих кодов, реализованных в полях Галуа. Поэтому целью работы является повышение надежности SPN-криптосистем за счет применения новых принципов кодирования модулярных кодов полиномиальной системы классов вычетов (ПСКВ).
Материалы и методы исследования
Одним из наиболее известных их представителей является шифр AES. Это итерационный блочный шифр, который реализует схему «квадрат». Блочный шифр AES нашел широкое применение благодаря хорошему сочетанию таких показателей, как криптографическая стойкость, производительность и относительно низкие схемные затраты.
С целью повышения надежности работы его шифратора в [10] предлагается свести шифрование из поля GF(28) к шифрованию в конечных полях меньшего порядка. В этом случае элементы поля Галуа GF(28) представляются в виде элементов полей GF(24). Такой переход позволяет использовать код ПСКВ с двумя информационными основаниями.
В полиномиальной системе классов вычетов двоичный код А = 10…11 представляется в полиномиальной форме A(z) = zm +…+ z + 1, а затем этому полиному в соответствие ставится набор остатков, полученных при делении этого кода на полиномы-основания [8, 9]:
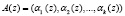, (1)
где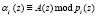 
; 
.
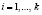Данный набор оснований кода ПСКВ образует рабочий диапазон
.
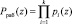Так как сравнения по одному и тому же модулю можно почленно складывать, вычитать и умножать, то для двух полиномов A(z) и B(z), имеющих соответственно коды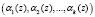 
и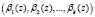 
, справедливо соотношение:
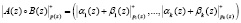. (2)
Параллельность обработки данных по основаниям ПСКВ позволяет обеспечить высокую скорость выполнения модульных операций. Благодаря этому свойству коды ПСКВ нашли широкое применение в системах реального масштаба времени [3–5]. При этом параллельная и независимая обработка остатков служат идеальной основой для построения процедур обнаружения и коррекции ошибок, возникающих из-за сбоев в работе системы [2, 6, 7].
Для коррекции ошибок с помощью модулярных кодов необходимо расширить рабочий диапазон до величины полного диапазона:
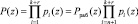. (3)
Для этого вводят избыточные основания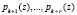 
, выбираемые из условия
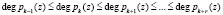, (4)
где deg pi(z) – степень неприводимого полинома pi(z); k – количество рабочих оснований.
Чтобы провести такую процедуру в модулярных кодах, применяют различные позиционные характеристики. Если основания ПСКВ являются основаниями обобщенной полиадической системы (ОПС), то имеем, что
.
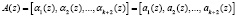Тогда, используя коэффициенты ОПС, можно представить
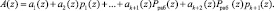(5)
Из равенства (5) видно, что если код ПСКВ принадлежит рабочему диапазону, то старшие коэффициенты ОПС, соответствующие контрольным основаниям, должны равняться нулю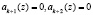 
. В работе [7] представлен алгоритм вычисления данной ПХ.
В работе [2] предлагается обнаруживать и корректировать ошибки на основе ПХ-интервала. В этом случае данная позиционная характеристика определяется
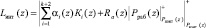, (6)
где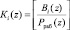 
; 
; 
.
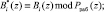
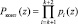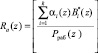В работе [6] представлен алгоритм вычисления ПХ – невязки контрольных остатков. Для получения данной ПХ вычисляют разность между значениями остатков α k + 1(z), αk + 2(z) по контрольным основаниям кода ПСКВ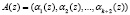 
и результатам вычисления остатков 
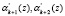с использованием рабочих оснований:
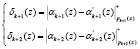, (7)
где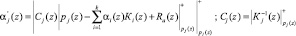 
; Ra(z) – ранг A(z) в безызбыточной ПСКВ; 
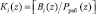; j = k + 1, k + 2.
Анализ рассмотренных алгоритмов показал, что классические принципы построения корректирующих модулярных кодов невозможно использовать для повышения надежности SPN-криптосистем. Это связано с тем, что для коррекции однократной ошибки в кодах ПСКВ используют два контрольных модуля. А в SPN-криптосистеме контрольным модулем может быть только полином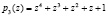 
. Значит, для проведения коррекции ошибок необходимо разработать новые принципы построения избыточных кодов ПСКВ.
Очевидно, что для коррекции однократной ошибки в модулярном коде необходимо наличие как минимум двух контрольных остатков αk + 1(z) и αk + 2(z). Первый остаток αk + 1(z) должен указывать глубину ошибки, т.е.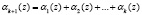 
. Если ошибка произошла по i-му основанию кода ПСКВ, то получаем
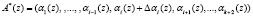, (8)
где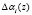 
– глубина ошибки по i-му основанию кода ПСКВ.
Тогда получаем, что
.
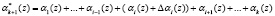Чтобы определить глубину ошибки, необходимо сложить эти остатки. Получаем
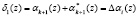. (9)
Второй остаток αk + 2(z) должен указать номер отказавшего основания. Тогда
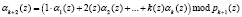, (10)
где i(z) – полиномиальная форма двоичного представления числа i.
Если ошибка произошла по i-му основанию кода ПСКВ, то остаток αk + 2(z) равен
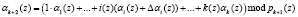. (11)
Чтобы определить номер отказавшего основания необходимо сложить эти остатки.
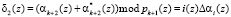. (12)
Очевидно, что если разделить значение δk + 2(z) на δk + 1(z), то результат дает i(z) – полиномиальную форму двоичного представления отказавшего канала. Таким образом, разработанный новый принцип построения избыточного кода ПСКВ с одним контрольным модулем позволяет корректировать ошибки, возникающие в процессе работы SPN-криптосистем.
Результаты исследования и их обсуждение
Шифр AES реализуется в GF(28) с использованием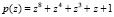 
. Предлагается вместо него использовать код ПСКВ с двумя основаниям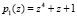и 
и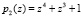 
. В качестве контрольного основания – 
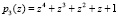. Рассмотрим применение разработанного принципа при проведении операции MixColums. В этом преобразовании столбцы состояния рассматриваются как многочлены над GF(28) и умножаются по модулю двучлена z4 + 1 на многочлен
.
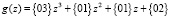При этом умножение байтов массива State на {02} и на {03} выполняются по модулю p(z). Пусть на вход преобразователя MixColums поступил 32-битовый столбец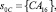 
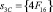
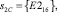
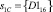. В избыточном коде ПСКВ эти байты, представленные в 16-ричной системе счисления, имеют вид {CA16} = (D, 2, F, 9), {D116}=(5,0,5,5), {E216} = (3, 1, 2,1), {4F16} = (3, 0, 3, 3). Рассмотрим получение нового значения байта:
.
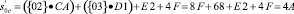При умножении первого байта СА на значение константы {02} получается байт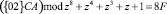 
. Представим данное произведение в коде ПСКВ с двумя информационными основаниям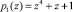и 
и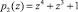 
. Получаем 
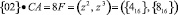. Вычислим значения двух контрольных остатков:
,
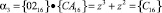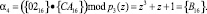
Тогда произведение можно записать в виде кода ПСКВ в следующем виде:
.
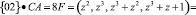
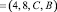Рассмотрим, как будет получен аналогичный результат с использованием соответствующих таблиц. Информационные остатки первого байта CA = (D, 2) поступают на входы табл. 1 и табл. 2. Представленная часть табл. 1 содержит остатки результата умножения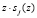 
, приведенной по модулям 
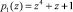. На пересечении второй строки и столбца D располагается 
.
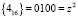Табл. 2 содержит результат умножения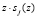 
по модулю 
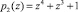. На пересечении второй строки и столбца D располагается остаток 
.
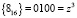Кроме того, информационные остатки первого байта CA = (D, 2) поступают на входы табл. 3 и табл. 4. Табл. 3 содержит данные о сумме остатков информационных оснований ПСКВ. На пересечении 2-й строки и столбца D находится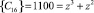 
.
В табл. 4 представлены данные о втором контрольном остатке. На пересечении второй строки и столбца D таблицы находится остаток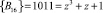 
.
Таким образом, после выполнения операции умножения первого байта имеем
.
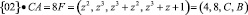Рассмотрим умножение второго байта состояния {D116} = (5, 0, 5, 5) на коэффициент на {03}. Получаем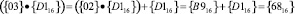 
. Тогда
; 
.
; 
.
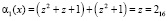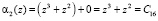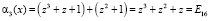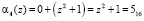Тогда результат умножения на константу {03} имеет вид
.
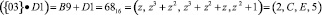При перемешивании столбцов MixColums получили новое состояние
.
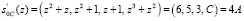Проведем проверку контрольных оснований. Получаем
; 
.
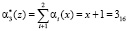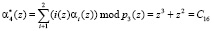Тогда синдром ошибки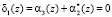 
; 
.
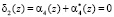Пусть из-за сбоя произошло искажение первого слагаемого на величину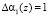 
. Тогда с выхода табл. 1 снимается 
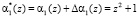, то есть комбинация
.
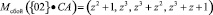В результате получили новое состояние:
.
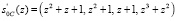Тогда остатки равны
; 
.
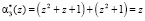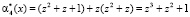Синдром ошибки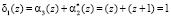 
; 
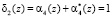. По значению синдрома ошибк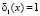и 
и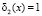 
из памяти берется вектор ошибки, который равен 
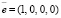, с помощью которого ошибка исправляется:
.
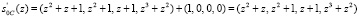Таблица 1
Остатки результата умножения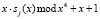 
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
F |
9 |
6 |
8 |
7 |
1 |
E |
E |
1 |
7 |
8 |
6 |
9 |
F |
0 |
|
1 |
D |
2 |
4 |
B |
5 |
A |
C |
3 |
3 |
C |
A |
5 |
B |
4 |
2 |
D |
|
2 |
D |
2 |
4 |
B |
5 |
A |
C |
3 |
3 |
C |
A |
5 |
B |
4 |
2 |
D |
|
3 |
… |
… |
… |
|||||||||||||
|
F |
D |
2 |
4 |
B |
5 |
A |
C |
3 |
3 |
C |
A |
5 |
B |
4 |
2 |
D |
Таблица 2
Остатки результата умножения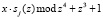 
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
C |
C |
0 |
0 |
C |
C |
0 |
C |
0 |
0 |
C |
C |
0 |
0 |
C |
|
1 |
E |
2 |
2 |
E |
E |
2 |
2 |
E |
2 |
E |
E |
2 |
2 |
E |
E |
2 |
|
2 |
8 |
4 |
4 |
8 |
8 |
4 |
4 |
8 |
4 |
8 |
8 |
4 |
4 |
8 |
8 |
4 |
|
3 |
… |
… |
… |
|||||||||||||
|
F |
B |
7 |
7 |
B |
B |
7 |
7 |
5 |
7 |
B |
B |
7 |
7 |
B |
B |
7 |
Таблица 3
Первый контрольный остаток α3(z)
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
3 |
5 |
6 |
8 |
B |
D |
E |
2 |
1 |
7 |
4 |
A |
9 |
F |
C |
|
1 |
3 |
0 |
6 |
5 |
B |
8 |
E |
D |
1 |
2 |
4 |
7 |
9 |
A |
C |
F |
|
2 |
5 |
6 |
0 |
3 |
D |
E |
8 |
B |
7 |
4 |
2 |
1 |
F |
C |
A |
9 |
|
3 |
… |
… |
… |
|||||||||||||
|
F |
6 |
5 |
3 |
0 |
E |
D |
B |
6 |
4 |
7 |
1 |
2 |
C |
F |
9 |
A |
Таблица 4
Второй контрольный остаток α4(z)
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
8 |
E |
6 |
8 |
0 |
6 |
E |
9 |
1 |
7 |
F |
1 |
9 |
F |
7 |
|
1 |
E |
6 |
0 |
8 |
6 |
E |
8 |
0 |
7 |
F |
9 |
1 |
F |
7 |
1 |
9 |
|
2 |
2 |
A |
C |
4 |
A |
2 |
4 |
C |
B |
3 |
5 |
D |
3 |
B |
D |
5 |
|
3 |
… |
… |
… |
|||||||||||||
|
F |
4 |
C |
A |
2 |
C |
4 |
2 |
9 |
D |
5 |
3 |
B |
5 |
D |
B |
3 |
Обобщая полученные результаты, можно сделать вывод о том, что разработанный алгоритм поиска и коррекции ошибок с помощью избыточного кода ПСКВ требует меньших схемных затрат на реализацию. Так, троированная мажоритарная система требует использования трех пар табл. 1 и 2 для маскирования ошибок, вызванных сбоями в шифраторе AES. А разработанные принципы построения избыточных кодов ПСКВ позволяет корректировать однократную ошибку с использованием четырех таблиц, приведенных в статье.
Заключение
Проведенный анализ известных алгоритмов обнаружения и исправления ошибок в модулярных кодах показал, что они не могут быть применены для повышения надежности работы SPN-криптосистем, так используют два контрольных основания. Исходя из особенностей реализации SPN-криптосистем в полях GF(24), в работе осуществлена разработка и исследование новых принципов построения избыточных кодов полиномиальной системы классов вычетов, позволяющих корректировать ошибки на основе использования одного контрольного основания. Показана возможность применения данных принципов при разработке новых модулярных кодов ПСКВ, способных корректировать ошибки, возникающие в процессе работы криптосистемы AES. Проведенные исследования показали, что применение разработанного алгоритма позволяет вычислять местоположение и глубину ошибки при меньших схемных затратах по сравнению с методом маскирования ошибок «2 из 3».
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-50081.