Экспериментальные исследования механических свойств наноматериалов показали, что предел прочности многих металлов (Pd, Сu, Ag, Ni и др.) значительно выше, чем в соответствующих массивных аналогах [1, 4]. Увеличение твердости и прочности с уменьшением размера зерна до некоторого критического размера практически характерно для всех кристаллов. Это вытекает из уравнения Холла – Петча, что предел текучести σТ зависит обратно пропорционально от среднего размера зерна d [4]:
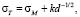 (1)
(1)
где σМ – предел прочности монокристалла, k – некоторый размерный коэффициент.
Соотношение (1) достаточно хорошо выполняется в широком диапазоне значений d вплоть до 1 мкм. Значения σТ, полученные экстраполяцией в область размера d < 100 нм, в 2–3 раза превышают таковые для традиционных материалов [1, 4]. Экспериментальные результаты, полученные на нанокристаллах, показывают, что они значительно прочнее крупнозернистых аналогов. Нанофазные Cu, Pd, Fe с размером зерна – 5 нм, полученные компактированием ультрадисперсных порошков, показали значения твердости в 2–5 раз выше, чем у образцов с обычным размером зерна.
Можно констатировать, что твердость металлов и керамических материалов возрастает по мере того, как размер зерна переходит в нанофазную область. Однако величина размера зерна, до которой происходит упрочнение, зависит от ряда факторов и природа этого явления не совсем ясна.
Прямой и обратный эффект Холла – Петча
Обычно соотношение Холла – Петча (1) выполняется для значительной части исследованных наноматериалов лишь до определенного размера зерна, а при более низких его значениях наблюдаются обратные эффекты: твердость (прочность) падает по мере снижения размера зерна.
В настоящее время не совсем ясно, соответствуют ли значения твердости, полученные для реальных компактированных наноматериалов, идеально плотным наносистемам. Поведение наноматериалов в данном случае может быть замаскировано вкладами от остаточной пористости – трещинами и другими дефектами, возникающими в наноматериалах вследствие особенностей методов их получения. Вопрос о природе микродефектов, возникающих в наноматериалах, и их роли в формировании свойств остается в значительной степени открытым. В частности, не совсем ясным является проявление дислокационного механизма в процессе деформации наноматериалов. Теоретическая трактовка уравнения Холла – Петча основывается на рассмотрении границ как барьеров для сдвига от зерна к зерну. Однако в наноразмерных зернах могут не реализовываться скопления дислокаций, достаточных для реализации сдвигового механизма деформации.
Несмотря на большое количество работ по исследованию влияния размерного фактора на механические свойства наноструктур, физические механизмы этого влияния остаются предметом продолжающихся дискуссий.
В работе [12] для предела текучести получено
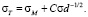 (2)
(2)
Уравнение (2) по форме совпадает с уравнением Холла – Петча (1). Однако коэффициенты пропорциональности в обеих формулах различаются. В рассматриваемом случае поведение предела текучести малых частиц определяется также величиной их поверхностного натяжения σ.
Поверхностное натяжение – основная характеристика процессов, связанных с участием поверхностей или границ раздела фаз. Поверхностное натяжение определяет свободную энергию (работу), которую необходимо затратить, чтобы образовать единицу площади поверхности или раздела фаз.
Наличие поверхностного натяжения обусловлено тем, что атомы на поверхности жидкости или твердого тела обладают большей потенциальной энергией, чем атомы или ионы внутри их, поэтому поверхностную энергию обычно рассматривают как избыток энергии, приходящейся на единицу площади.
Экспериментальное определение поверхностного натяжения твердых тел затруднено тем, что их молекулы (атомы) лишены возможности свободно перемещаться. Исключение составляет пластическое течение металлов при температурах, близких к точке плавления. Вследствие анизотропии кристаллов поверхностное натяжение на разных гранях кристалла различно. Понятия поверхностного натяжения и свободной поверхностной энергии для твердых тел не тождественны. Дефекты кристаллической решётки, главным образом дислокации, рёбра и вершины кристаллов, границы зёрен поликристаллических тел, выходящие на поверхность, вносят свой вклад в свободную поверхностную энергию. Поверхностное натяжение твердых тел обычно определяют косвенно, исходя из межмолекулярных и межатомных взаимодействий. В работе [13] предложены прямые методы определения поверхностного натяжения наночастиц и нанопленок.
Для малых d А.И. Русанов получил асимптотическую линейную зависимость [8]:
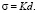 (3)
(3)
Здесь К – коэффициент пропорциональности. Формула (3) получена на основе термодинамического рассмотрения и должна быть применима к малым объектам различной природы. В этом случае уравнение (2) принимает вид
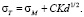 (4)
(4)
Уравнение (4) представляет собой обратный эффект Холла – Петча.
Критический радиус
Рассмотрим теперь вопрос о размере металлической наночастицы, начиная с которого прямой эффект Холла – Петча сменяется на обратный, т.е. упрочнение наночастиц сменяется их разупрочнением. Из уравнения (2) следует, что уравнение Холла – Петча начинает нарушаться с того момента, когда начинает проявляться размерная зависимость поверхностного натяжения. Экспериментально критический радиус наночастицы можно определить по размерной зависимости ее температуры плавления [13] или по размерной зависимости какого-либо другого физического свойства [14]. Рассчитанные в работе [13] значения критического радиуса для большинства металлов таблицы Менделеева приведены в табл. 1.
Из табл. 1 видно, что критический радиус чистых металлов не превышает 10 нм. Например, для вольфрама критический радиус равен 8,4 нм, т.е. в пределах ошибок эксперимента он совпадает с экспериментальным значением, приведенным в работе [5].
Влияние границ зерен на механические свойства наноматериалов
Значительное влияние на механические свойства наноматериалов оказывают границы зерен. Прямые наблюдения методом просвечивающей электронной микроскопии высокого разрешения показали, что структура границ зерен наноматериалов подобна структype высокоугловых границ. Важным фактором, определяющим деформационное поведение наноматериалов, являются внyтpенние напряжения, наличие которых обусловлено большим числом близко расположенных границ зерен и тройных стыков зерен, а также особенностями методов получения наноматериалов. Прочность при растяжении нанокристаллического никеля (размер зерна 100 нм), полученного методом экструзии, превышает прочность крупнозернистого аналога в 1,7 раза. Прочность при растяжении нанокристаллического золота (размер зерна 36 нм), полученного методом конденсации из паровой фазы, превышает прочность крупнозернистого золота в три раза.
В работах [6, 10] рассмотрено несколько моделей:
– модель «скоплений», объясняющая влияние размера зерна на σт концентрацией напряжений в скоплениях дислокаций, моделирующих индивидуальные полосы скольжения;
– модели деформационного упрочнения, объясняющие соотношение (1) зависимостью плотности дислокаций или длины их пробега от размера зерна;
– модель, использующая представление об особенностях механизмов работы поверхностных или зернограничных дислокационных источников в процессе передачи скольжения от зерна к зерну;
– модель, базирующаяся на представлениях о двух типах дислокаций – статически запасенных и геометрически необходимых.
Указанные модели позволяют качественно объяснить степенной характер зависимости предела текучести от размера зерна в предположении о постоянстве параметра К. Вместе с тем, к настоящему времени накоплен большой объем экспериментальных данных, которые не удается интерпретировать в рамках традиционных представлений о постоянстве параметра К. В частности, в ряде экспериментальных работ обнаружена существенная зависимость коэффициента К от степени и скорости предварительной деформации, температуры и времени предварительного дорекристаллизационного отжига и т.д.
Вопрос о вкладе зернограничного проскальзывания в общую долю деформации НМК металлов (при комнатной температуре) также весьма неоднозначен и спорен и до настоящего времени остается открытым.
В работе [5] показано, что существует около десятка различных моделей, которые не до конца могут объяснить нарушение закона Холла – Петча при размерах зерен меньше критического. Считается, что традиционная деформация по дислокационному механизму в материалах с размером зерна меньше 30 нм невозможна ввиду малой вероятности появления подвижных дислокаций.
Нарушение закона Холла – Петча экспериментально исследовано в работе [11] и теоретически в работе [3], а также во многих других работах.
Примером компьютерного моделирования является работа [7], где в рамках инженерии границ зерен выявлены два типа ротационно-волновых потоков, которые определяются углом разориентации смежных зерен. Первый тип зернограничных потоков развивается в малоугловых границах и генерирует в объем зерен дислокации, определяющие прямой эффект Холла – Петча. Второй тип зернограничных потоков развивается в большеугловых границах и приводит к обратному эффекту Холла – Петча.
Таблица 1
Критический радиус частиц чистых металлов (М)
|
М |
r, нм |
М |
r, нм |
М |
r, нм |
М |
r, нм |
М |
r, нм |
М |
r, нм |
М |
r, нм |
|
Li |
1,4 |
Sr |
8,3 |
Sn |
2,0 |
Cd |
1,9 |
Fe |
3,1 |
Gd |
7,6 |
Ac |
7,1 |
|
Na |
2,1 |
Ba |
8,9 |
Pb |
2,6 |
Hg |
0,8 |
Co |
2,8 |
Tb |
7,5 |
Th |
9,6 |
|
K |
3,7 |
Al |
2,2 |
Se |
1,9 |
Cr |
3,8 |
Ni |
2,7 |
Dy |
7,6 |
U |
4,2 |
|
Rb |
4,2 |
Ga |
0,9 |
Te |
3,5 |
Mo |
6,5 |
Ce |
5,4 |
Ho |
7,8 |
Np |
2,6 |
|
Cs |
5,2 |
In |
1,6 |
Cu |
2,3 |
W |
8,4 |
Pr |
6,0 |
Er |
7,8 |
Pu |
2,7 |
|
Be |
1,8 |
Tl |
2,4 |
Ag |
3,1 |
Mn |
2,8 |
Nd |
6,4 |
Tm |
7,4 |
Am |
6,4 |
|
Mg |
3,1 |
Si |
4,9 |
Au |
3,3 |
Tc |
5,1 |
Sm |
6,3 |
Yb |
6,5 |
Bk |
5,2 |
|
Ca |
7,0 |
Ge |
4,0 |
Zn |
1,5 |
Re |
7,1 |
Eu |
8,3 |
Lu |
8,2 |
– |
– |
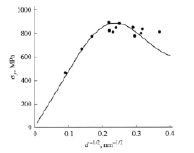
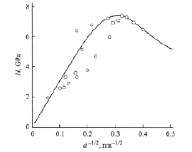
а)б)
Соотношение Холла – Петча для предела текучести нанокристаллической меди (а) и микротвердости никеля (б) [2]
Таблица 2
Предельная текучесть микро- и наночастиц некоторых металлов
|
Металл |
σ0, МПа [9] |
σ, Дж/м2 |
σ Т, МПа d = 16 нм |
σТ, МПа d = 64 нм |
σТ, МПа d = 100 нм |
σТ, МПа d = 225 нм |
|
Алюминий |
22 |
0,653 |
38 |
30 |
28 |
26 |
|
Бериллий |
230 |
1,091 |
257 |
244 |
241 |
237 |
|
Ванадий |
106 |
1,512 |
144 |
125 |
121 |
112 |
|
Вольфрам |
760 |
2,587 |
825 |
792 |
786 |
777 |
|
Гафний |
500 |
1,754 |
544 |
529 |
518 |
507 |
|
Железо |
170 |
1,268 |
202 |
186 |
189 |
178 |
|
Золото |
40 |
0,936 |
64 |
56 |
49 |
44 |
|
Иридий |
90–100 |
1,917 |
138–148 |
122–132 |
109–119 |
98–108 |
|
Ниобий |
210 |
1,919 |
258 |
242 |
229 |
218 |
|
Палладий |
60 |
1,279 |
92 |
81 |
73 |
65 |
|
Платина |
70 |
1,429 |
106 |
94 |
84 |
76 |
|
Родий |
70–100 |
1,567 |
109–139 |
96–126 |
86–116 |
76–106 |
|
Рутений |
300–400 |
1,825 |
346–446 |
331–431 |
318–418 |
307–407 |
|
Серебро |
20–30 |
0,865 |
42–52 |
35–45 |
29–39 |
23–33 |
Расчет предела текучести изолированных металлических наночастиц
На рисунке показаны зависимости Холла – Петча (ХП) для меди и никеля.
Обработка кривых рисунка с помощью соотношения (2) дала значение постоянной С:
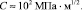 (5)
(5)
Необходимо отметить следующее: постоянная С имеет одно и то же значение для большинства металлов периодической системы элементов. Это позволяет объяснить наблюдаемую зависимость коэффициента К в уравнении (2) от типа металла через различие в величине поверхностного натяжения для различных металлов.
Используя табличные данные по величине σМ [9] и определяя величину поверхностного натяжения по методике [13], мы можем рассчитать предел текучести для тех металлов, для которых известна величина σМ.
Для ряда металлов результаты таких расчетов приведены в табл. 2.
Из табл. 2 следует, что предел текучести для частиц размером (0,3–0,5) микрон практически совпадает с соответствующей величиной для массивного образца.
Заключение
В настоящее время механические свойства наночастиц и наноматериалов экспериментально исследуются интенсивно, благодаря развитию методов атомно-силовой микроскопии и наноиндентирования. Эти методы позволяют определять твердость наночастиц и наноматериалов, модули упругости и Юнга, предел текучести и т.д.
Особенно большой интерес к исследованию механических свойств наночастиц появился в последнее время в связи с конструированием композиционных материалов и оптимизацией их характеристик, которые определяются на основе свойств наноэлементов, входящих в их состав. Поэтому нахождение упругих свойств, структурно-масштабных и энергетических параметров наночастиц представляет собой фундаментальный и практический интерес.
Работа выполнена по программе МОН РК 055 «Научная и/или научно-техническая деятельность», подпрограмма 101 «Грантовое финансирование научных исследований».



