Техническая эксплуатация оборудования системы электроснабжения (СЭС) предполагает поддержание показателей надежности на требуемом уровне за счет своевременного обнаружения неисправностей и их дальнейшего устранения, выявления степени ухудшения эксплуатационных показателей, проведение предупредительных ремонтов. Оптимальная система эксплуатационного обслуживания элементов СЭС позволяет установить объем и сроки проведения работ, связанных с поддержанием готовности системы при минимальных затратах.
В настоящее время система технической эксплуатации СЭС основана на жесткой стратегии технического обслуживания и ремонта (ТО и Р). Применение данной стратегии в современных условиях (возросшая надежность элементной базы, применение современных систем контроля и диагностирования, систем автоматизированного управления, возросшие требования к надежности СЭС и качеству электроэнергии, ограничения людских и материальных ресурсов) приводит к неоправданному простою оборудования, росту числа эксплуатационно-ремонтного персонала, ухудшению технико-экономических показателей электрооборудования. Все это делает актуальным вопрос пересмотра существующей системы эксплуатации и перехода к гибкой системе ТО [5]. Данный переход обеспечивается возможностями применения элементов технологии SMART GRID, на базе которых в рамках энергетической стратегии России до 2030 года планируется создание высокоинтегрированных интеллектуальных сетей [1].
Определения значений параметров технического обслуживания (ТО) СЭС, таких как периодичность работ по ТО, количество и тип средств, выводимых на ТО, предполагает сравнение различных вариантов организации ТО СЭС по ряду показателей, характеризующих величину затрат и достигаемые при этом полезные результаты. В качестве таких показателей целесообразно использовать следующие основные группы показателей, описываемые векторами: 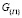 – вектор показателей надежности СЭС, ее функциональных подсистем и отдельных средств;
– вектор показателей надежности СЭС, ее функциональных подсистем и отдельных средств; 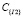 – вектор стоимостных показателей, характеризующих затраты на реализацию процедур ТО СЭС.
– вектор стоимостных показателей, характеризующих затраты на реализацию процедур ТО СЭС.
Целесообразность выбора того или иного варианта проведения ТО обусловливается требованиями, предъявляемыми к СЭС в целом. При этом стремятся к тому, чтобы обеспечивать как можно лучшие значения по всем показателям качества и при этом значения ни одного из показателей не оказались хуже заданных предельно допустимых значений.
Решение данной задачи целесообразно осуществлять с помощью нахождения множества эффективных (Парето-оптимальных) решений и последующего выбора компромиссного варианта.
Будем считать заданными:
– 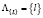 – множество дат начала ТО обслуживаемой СЭС, где l – даты начала очередного ТО,
– множество дат начала ТО обслуживаемой СЭС, где l – даты начала очередного ТО, 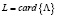 – мощность множества
– мощность множества 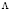 ;
;
– 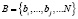 – множество обслуживаемых элементов СЭС;
– множество обслуживаемых элементов СЭС;
– N – количество обслуживаемых элементов СЭС;
– Ni – множество элементов СЭС i-го вида, 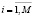 ;
;
– М – количество видов элементов СЭС с однотипными операциями ТО;
– vi – производительность бригад обслуживающего персонала (максимально допустимое количество обслуживаемых элементов СЭС i-го вида за один день).
Введем булеву переменную xlj, являющуюся переменной в задаче выбора значений ТО:
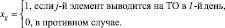
Необходимо выбрать такой вариант значений параметров ТО 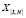 , при котором достигаются оптимальные значения выбранных показателей качества функционирования (ПКФ):
, при котором достигаются оптимальные значения выбранных показателей качества функционирования (ПКФ):
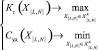 (1)
(1)
При ограничениях:
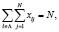 (2)
(2)
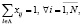 (3)
(3)
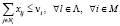 . (4)
. (4)
Задача выбора оптимальных значений параметров ТО в постановке (1–4) относится к классу многокритериальных задач целочисленного программирования, а точнее, к задаче комбинаторного булева программирования. Для ее решения необходимо выполнить следующие этапы:
1. Сужение множества анализируемых вариантов.
2. Формирование множества Парето-оптимальных решений.
3. Выбор компромиссного варианта значений параметров ТО.
Алгоритм сужения множества анализируемых вариантов значений ТО
Для нахождения оптимального значения 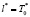 по каждому из введенных критериев необходимо решить относительно T0 уравнения
по каждому из введенных критериев необходимо решить относительно T0 уравнения
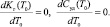 (5)
(5)
Для решения данной задачи предлагается использовать метод, основанный на сочетании методов «золотого сечения» и параболической интерполяции [2, 6].
В результате формируется множество дат ТО 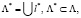 где l* – календарный день начала ТО элемента СЭС, при котором достигается оптимальное значение показателей качества функционирования. Далее из множества
где l* – календарный день начала ТО элемента СЭС, при котором достигается оптимальное значение показателей качества функционирования. Далее из множества 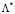 исключаются даты, в которые вывод элемента СЭС на ТО запрещен.
исключаются даты, в которые вывод элемента СЭС на ТО запрещен.
На следующем этапе группируются элементы СЭС с однотипными операциями ТО. Для этого осуществляется перегруппировка множества номеров столбцов матрицы 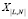 , таким образом, чтобы
, таким образом, чтобы 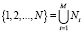 , – множество видов элементов СЭС с однотипными операциями ТО.
, – множество видов элементов СЭС с однотипными операциями ТО.
Таким образом формируется сложное множество вариантов значений параметров ТО 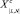 . В дальнейшем за L принимается мощность суженного множества возможных дат начала очередных ТО элементов СЭС
. В дальнейшем за L принимается мощность суженного множества возможных дат начала очередных ТО элементов СЭС 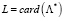 .
.
Формирование множества Парето-оптимальных вариантов значений параметров ТО
Определение множества эффективных решений 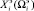 можно формально записать следующим образом:
можно формально записать следующим образом:
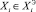 ,
,
если
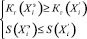 , (6)
, (6)
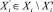 , и хотя бы одно из неравенств (6) окажется строгим.
, и хотя бы одно из неравенств (6) окажется строгим.
Нахождения множества эффективных решений на основе метода последовательного сужения множества альтернатив [6] осуществляется в несколько этапов:
На подготовительном этапе осуществляется выбор решения 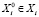 для построения множества
для построения множества 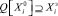 . Точка
. Точка 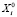 выбирается из множества
выбирается из множества 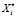 :
:
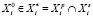 ,
,
где
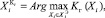
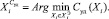
Этап № 1. Строится множество 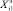 . Процедуры выполняются итеративно, число итераций на каждом этапе конечно, но заранее неизвестно.
. Процедуры выполняются итеративно, число итераций на каждом этапе конечно, но заранее неизвестно.
Начальная итерация: полагаем 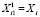 . j-я итерация: находим множество
. j-я итерация: находим множество
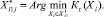
Из множества 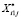 выделяем подмножество
выделяем подмножество 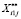 , содержащее все точки, удовлетворяющие условиям.
, содержащее все точки, удовлетворяющие условиям.
Формируем множество 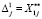 . Сужаем множество альтернатив
. Сужаем множество альтернатив 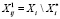 .
.
Поскольку 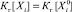 , то переходим ко второму этапу, принимая в качестве множества альтернатив
, то переходим ко второму этапу, принимая в качестве множества альтернатив 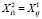 .
.
Этап № 2. Начальная итерация: решаем задачу:
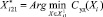 .
.
Находим
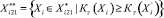 .
.
Присваиваем переменной Кгmax значение Кг(Xi)
 .
.
Формируем множество 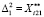 .
.
Поскольку 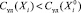 , то переходим ко второй итерации, j = 2
, то переходим ко второй итерации, j = 2
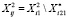 .
.
Решаем задачу
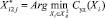 .
.
Формируем множество
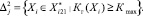
Если 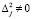 , то присваиваем переменной значение
, то присваиваем переменной значение
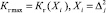 .
.
Сужаем множество альтернатив
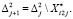
Если 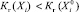 , то j = j + 1.
, то j = j + 1.
Если 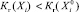 , то
, то 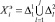 .
.
Таблица 1
Перечень оборудования СЭС
|
Исходные данные |
Высоковольтные выключатели, 24 шт. |
АВР, 4 шт |
Трансформаторы, 25 шт. |
Автоматические высоковольтные переключатели, 25 шт. |
Рубильники низковольтные, 25 шт. |
|
Среднее кол-во отказов N |
21 |
15 |
19 |
18 |
21 |
|
τВ, час |
1,89 |
2,12 |
2,29 |
2,11 |
2,4 |
|
τТО, час |
4 |
5 |
3 |
5 |
5 |
|
Тотк, час |
329 |
400 |
398 |
401 |
415 |
Отметим, что на каждой итерации решаются оптимизационные задачи с использованием алгоритма целенаправленного перебора вариантов, причём на каждой итерации происходит сужение множества альтернатив, т.е.
card(Xij) < card(Xi(j-1)).
Выбор компромиссного варианта значений параметров ТО
Компромиссным решением многокритериальной задачи дискретной оптимизации является такое эффективное решение, для которого взвешенные относительные потери (отклонения от оптимумов) по всем частным показателям одинаковы и минимальны [3], т.е.
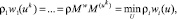 (7)
(7)
где М – множество частных показателей качества, ρi – весовые коэффициенты относительной важности частных показателей эффективности функционирования системы в целом, удовлетворяющие условиям 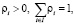
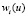 – относительные отклонения от оптимумов показателей качества функционирования на значениях параметров
– относительные отклонения от оптимумов показателей качества функционирования на значениях параметров 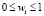 .
.
Относительные отклонения от оптимумов определяются следующим образом:
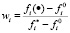 , (8)
, (8)
где 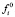 и
и 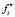 – соответственно оптимальное и наихудшее значения i-го показателя качества, достигаемые на множестве вариантов решений с учетом ограничений.
– соответственно оптимальное и наихудшее значения i-го показателя качества, достигаемые на множестве вариантов решений с учетом ограничений.
Определение весовых коэффициентов относительной важности является самостоятельной задачей. В данной работе они предполагаются заданными.
Согласно [3] нахождение компромиссного решения может быть сведено к решению следующей задачи:
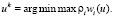 (9)
(9)
Таким образом, решением задачи определения варианта значений параметров ТО СЭС является такой набор значений параметров ТО, при котором максимальное взвешенное отклонение от оптимума на множестве показателей является минимальным.
Анализ эффективности предложенной методики определения объемов и моментов начала ТО был проведен на основе сравнения значений коэффициента готовности и средних удельных затрат на эксплуатацию за 12 месяцев при различных стратегиях обслуживания СЭС на одном из действующих объектов. В качестве исходных данных для проведения расчетов взята статистика по отказам элементов СЭС, накопленная за 12 месяцев эксплуатации. Эти данные приведены в табл. 1.
Результаты сравнения приведены в табл. 2.
Таблица 2
Результаты перехода к стратегии технического обслуживания по состоянию
|
ПКФ |
Стратегии ТО |
|
|
Жесткая |
Гибкая |
|
|
Кг |
0,9834 |
0,993 |
|
Трудозатраты, чел/час |
48 |
19,2 |
|
Матер. средства, усл/ед. |
6 |
1 |
Из табл. 2 видно, что при переходе к гибкой стратегии технического обслуживания значения выбранных показателей качества функционирования системы эксплуатации СЭС возрастают.
Заключение
Полученные результаты свидетельствуют о возможности перехода к гибким стратегиям технического обслуживания СЭС на основе предлагаемого подхода. Реализация данной стратегии позволяет экономить людские и материальные ресурсы, а также удовлетворять требованиям, предъявляемым к надежности функционирования СЭС объектов.



