В настоящее время продолжает быть актуальной проблема решения многокритериальных оптимизационных задач. В таких задачах необходимо учесть достаточно большое количество критериев или параметров, причем не просто учесть, а выстроить их в каком-либо порядке – ранжировать или определить приоритетность. Как правило, такого рода задачи встречаются при аналитическом планировании, построении систем принятия решения, оценке инновационных проектов, предварительном проектировании систем различного назначения [7, 9].
При решении вышеуказанных задач хорошо зарекомендовал себя метод анализа иерархий (МАИ), разработанный американским математиком Томасом Саати [3, 13]. Данный метод основан на парном сравнении критериев или параметров на каждом уровне иерархии и, соответственно, выстраивании локальных векторов приоритетов, а затем формировании на их основе глобального или обобщенного вектора приоритетов.
Достоинством МАИ является высокая универсальность, наглядность, способность учитывать любое количества критериев или параметров, а также возможность безболезненно для общего решения рассматриваемой задачи добавлять и убирать факторы либо критерии. МАИ достаточно популярен. На его основе пишутся различные программные продукты, к примеру «MPRIORITY 1.0» [12].
Однако наличие в МАИ элементов, зависящих от субъективного мнения экспертов, в конечном итоге вносит некоторую неточность. Также могут возникнуть трудности с согласованностью выдаваемых экспертами оценок, коэффициентом конкордации и, наконец, с тем, как множество оценок экспертов «привести к общему знаменателю». Если рассматривать согласованность и коэффициент конкордации, то здесь все зависит от того, насколько качественно подобрана группа экспертов, а также насколько они компетентны в рассматриваемом вопросе. Что касается «приведения к общему знаменателю», то обычно эта проблема решается усреднением значений, другими словами, складываются все оценки и делятся на количество экспертов, участвующих в опросе.
Авторами статьи предлагается модификация известного метода анализа иерархий, которая будет заключаться во введении индекса достоверности (ИД) и дифференцированной шкалы относительной важности. Всем известно, что на мыслительную деятельность человека и возможность принятия им адекватных решений влияют различные факторы. Эксперт не является исключением. В связи с этим, для повышения точности получаемых результатов, предлагается ввести индекс достоверности. Он будет формироваться на основе индекса согласованности, отвечающего за числовую и транзитивную согласованность. Также предлагается заменить шкалу относительной важности, разработанную Т. Саати, на дифференцированную шкалу, оценки в которой будут получаться из прямых или обратных отношений характеристик или параметров, посчитанных для той или иной альтернативы.
Так как в целом МАИ предназначен для поиска глобального приоритета, то в общем виде его можно представить как решение задачи максимизации. Другими словами, глобальный вектор приоритетов определяет максимально выгодное значение среди возможных альтернатив. В таком случае, если брать прямые отношения характеристик или параметров альтернатив, то в результате всех операций в приоритете будут те альтернативы, которые обладают наибольшими показателями характеристик или параметров. Как же быть, если необходимо выделить в приоритет альтернативы с меньшими показателями, т.е. решить задачу минимизации. В таком случае, когда применяется дифференцированная шкала относительной важности, авторами статьи предлагается производить транспонирование матрицы оценок, для того чтобы альтернативы с минимальными показателями характеристик или параметров оказывались в приоритете.
Предложенную модификацию метода анализа иерархий предлагается рассмотреть на примере решения многокритериальной задачи по поиску оптимальной структуры энергетической системы перспективной гидравлической установки для наземного технического обслуживания летательных аппаратов различного типа. В данном случае под энергетической системой будут подразумеваться все элементы, участвующие в преобразовании энергии от источника до потребителя. К примеру, в качестве источника может выступать двигатель внутреннего сгорания, а конечным потребителем будет гидравлический насос. Условия задачи требуют выбрать структуру энергетической системы перспективной гидравлической установки с минимальной потребляемой мощностью, минимальной стоимостью и массой, а также с максимальной удельной мощностью и коэффициентом полезного действия (КПД).
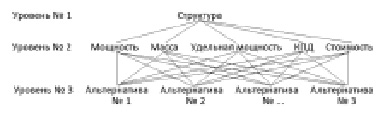
Рис. 1. Декомпозиция решаемой задачи на уровни и представление в виде доминантной иерархии
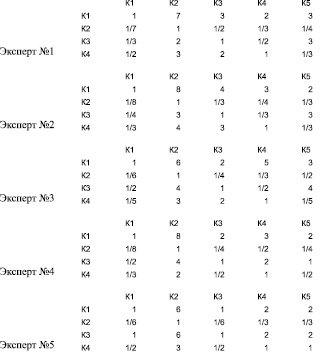
Рис. 2. Матрицы 2-го уровня оценок экспертов. Примечание. К1 – мощность, К2 – масса, К3 – удельная мощность, К4 – КПД, К5 – стоимость
Проведем декомпозицию задачи и представление её в виде иерархии, где на первом (высшем) уровне находится цель – структура энергетической системы перспективной гидравлической установки. На втором уровне пять критериев, уточняющих цель, и на третьем уровне располагаются альтернативные варианты структур, которые будут оценены по отношению к критериям второго уровня (рис. 1) [6].
Составляем матрицу парных сравнений 2-го уровня по пяти критериям. Так как в нашем примере на данном уровне иерархии невозможно определить степень важности одного критерия над другим, например стоимости над мощностью, то необходимо прибегнуть к опросу группы экспертов с целью получения оценок по шкале относительной важности, разработанной Т. Саати [8, 10, 11]. Коллективом экспертов из пяти человек, были выставлены следующие оценки относительной важности критериев (рис. 2).
Каждая из полученных матриц обладает индексом согласованности (ИС), который дает информацию о степени нарушения кардинальной (численной) и транзитивной (порядковой) согласованности [5]. ИС вычисляется по следующей формуле:
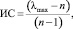(1)
где λmax – максимальное собственное значение матрицы, n – размерность матрицы.
Как известно, измерения подвержены как объективным, так и субъективным погрешностям. В целом наличие такого рода погрешностей может привести к несогласованным (противоречивым) выводам. К примеру, при взвешивании предметов измерения могут показать, что А тяжелее, чем Б, Б тяжелее В, однако В тяжелее А. Такое может произойти, когда веса предметов близки, а измерительный прибор недостаточно точен. Или другой случай, когда эксперт, отвечая на вопрос: «Какова приоритетность критерия мощности над критерием массы?», присваивает ему значение 6/1. Затем отвечая на вопрос: «Какова приоритетность критерия мощности над критерием КПД?», присваивает ему значение 2/1. Далее, ответив еще на десяток подобных вопросов, скорее всего, не учтет соотношений 6/1, 2/1 и на вопрос «Какова приоритетность критерия КПД над критерием массы?» ответит, исходя из каких-то внутренних (подсознательных) соображений, например, 2/1. Однако, если к данному вопросу подойти строго математически, то необходимо было ответить 3/1, так как
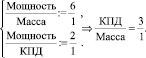(2)
Таким образом, чем большее факторов, мешающих эксперту ответить максимально точно и сосредоточенно, а также, чем меньшее он компетентен в конкретном вопросе, тем больше у него будет величина ИС. Поэтому ИС логичнее было назвать индекс рассогласованности, но это прерогатива автора МАИ – Т. Саати. Так же необходимо упомянуть об индексе отношения согласованности (ОС) – это тот же ИС, но отнесенный к индексу случайной согласованности матрицы (СС). Индекс СС представляется табличными значениями и посчитан для матриц различной размерности, заполненных случайными числами. К примеру, если ОС составляет более 20 %, с учетом необходимой точности решения поставленной задачи, рекомендуется пересмотреть ответы данные экспертом и скорректировать их в сторону уменьшения ОС до значений хотя бы меньших 20 %.
Предлагаемая авторами статьи модификация направлена на снижение влияния ответов экспертов с большим индексом согласованности на конечный результат многокритериальной оптимизационной задачи. Уменьшение указанного влияния предлагается осуществлять через введение индекса достоверности. Получать данный индекс предлагается следующим образом:
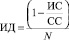, (3)
где ИД – индекс доверия, ИС – индекс согласованности, СС – индекс случайной согласованности, N – количество экспертов, участвовавших в опросе.
Теперь рассмотрим, как же встраивается предложенный индекс достоверности (ИД) в общий алгоритм МАИ. Из группы матриц 2-го уровня, полученных в результате опроса экспертов, формируем набор локальных приоритетов оценок экспертов, которые выражают относительное превосходство одних критериев над другими в соответствии с мнением конкретного эксперта. Получаем следующие векторы локальных приоритетов оценок экспертов:
|
Эксперт № 1 |
Эксперт № 2 |
Эксперт № 3 |
Эксперт № 4 |
Эксперт № 5 |
|
|
|
|
|
|
Мы не будем вдаваться в подробности, как из матрицы оценок получить вектор приоритетов, так как это достаточно хорошо описано в работах [1–4], поэтому продолжим рассмотрение задачи далее. В классическом варианте МАИ из пяти полученных векторов локальных приоритетов оценок экспертов необходимо получить один обобщенный вектор путем усреднения:
. (4)
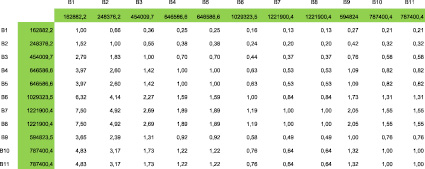Рис. 3. Матрица парных сравнений альтернатив по критерию стоимости
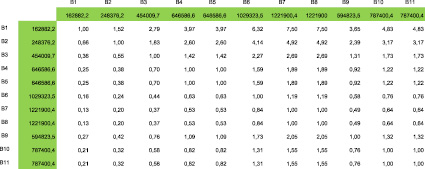
Рис. 4. Транспонированная матрица оценок альтернатив по критерию стоимости
Однако авторами статьи предлагается следующая модификация МАИ. Сначала необходимо подсчитать ИС для каждой матрицы оценок соответствующего эксперта. Вычисление ИС достаточно трудоемкий итерационный процесс, в первую очередь связанный с необходимостью вычисления максимального собственного числа матрицы. В связи с этим в рамках данной статьи подсчет ИС нецелесообразен, поэтому мы его пропустим и представим готовые значения для каждой матрицы оценок экспертов соответственно: ИС № 1= 0,19; ИС № 2 = 0,23; ИС № 3 = 0,31; ИС № 4 = 0,005; ИС № 5 = 0. Далее используя (3) и табличное значение индекса случайной согласованности (для матриц размерностью 5×5 СС = 1,12), получим индексы достоверности, из которых сформируем вектор доверия:
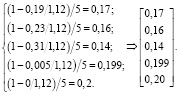(5)
Затем из векторов локальных приоритетов оценок экспертов формируем матрицу m×n, где m – число строк равное числу строк в векторе локального приоритета оценок соответствующего эксперта, а n – число столбцов равное числу экспертов, участвовавших в опросе. После чего умножаем получившуюся матрицу на вектор доверия и получаем общий локальный вектор приоритетов оценок экспертов скорректированный с учетом индекса достоверности:
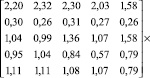
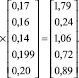(6)
Вектор локальных приоритетов оценок экспертов (4) и вектор (6), уточненный индексом достоверности, приблизительно равны. Однако вектор (6) представлен значениями со сниженным уровнем влияния оценок экспертов, у которых относительно большой индекс согласованности. Тем самым повышается точность обобщенного локального вектора приоритетов оценок экспертов в десяти- или двадцатипроцентном «коридоре» в зависимости от условий решаемой задачи.
Далее рассмотрим применение дифференцированной шкалы относительной важности при сравнении альтернатив в матрице 3-го уровня по пяти критериям. Как отмечалось выше, в МАИ на всех уровнях иерархии применяется шкала относительной важности, разработанная Т. Саати. В таких случаях распределение приоритетности альтернатив зависит лишь от мнения эксперта. С целью снижения влияния субъективности мнений экспертов авторами статьи предлагается вместо оценок экспертов использовать оценки, получаемые посредством взятия прямых и обратных отношений характеристик или параметров сравниваемых альтернатив. Такой подход позволяет управлять степенью влияния ЛПР на конечный результат. Здесь под степенью влияния подразумевается, какие данные в таблице парных сравнений будет использовать ЛПР. Возможно, оно будет в большей степени опираться на данные, полученные от субъективных высказываний приглашенных экспертов, и в меньшей – на статистические данные, параметры и характеристики. Также возможна обратная ситуация, когда ЛПР попытается максимально снизить влияние субъективных мнений экспертов и по возможности работать с сухими статистическими данными. Шкалу относительной важности в таком случае целесообразно назвать дифференцированной, так как она формируется по каждому критерию отдельно, исходя из минимального и максимального значения параметра или характеристики соответствующей альтернативы. Построим матрицу 3-го уровня, в которой сравниваются альтернативы по критерию стоимости, применяя дифференцированную шкалу относительной важности (рис. 3).
Исходя из представленной на рис. 3 матрицы получаем следующий вектор локального приоритета по критерию стоимости:
(7)
Как видно из рис. 3 и вектора (7), в приоритет выдвигается альтернатива с максимальной стоимостью, что является в общем виде следствием реализации классического подхода МАИ к решению задачи максимизации. Для того, чтобы выдвинуть в приоритет альтернативу с меньшей стоимостью, при решении задачи с использованием дифференцированной шкалы относительной важности необходимо провести транспонирование полученной матрицы оценок альтернатив (рис. 4).
После транспонирования вектор локального приоритета по критерию стоимости примет вид
(8)
Как видно из вектора (8), приоритеты перераспределились и максимальное значение стало принадлежать альтернативе с минимальной стоимостью, что и требовалось по условию задачи. В остальном решение задачи принимает классический вид МАИ и поэтому в рамках данной статьи не требует дальнейшего рассмотрения.
Таким образом, предложенная модификация известного метода анализа иерархий в части введения индекса достоверности позволяет скорректировать оценки экспертов и тем самым повысить точность получаемых результатов при формировании обобщенного локального приоритета экспертов. В свою очередь использование дифференциальной шкалы относительной важности с операцией транспонирования дает возможность решить в комплексе задачу максимизации и минимизации, что отсутствовало в классическом варианте МАИ. При этом на третьем уровне иерархии при сравнении альтернатив исключаются элементы субъективности, возникавшие из оценок экспертов.