Одним из путей повышения надежности функционирования систем электроснабжения (СЭС) является широкое внедрение в процесс их эксплуатации средств и методов диагностирования электрооборудования (ЭО), позволяющих выявлять возникающие в нем дефекты на ранних стадиях их развития и оценивать техническое состояние оборудования в периодах между ремонтами, в том числе и без вывода его из эксплуатации. При этом возникает необходимость предварительной оценки влияния вводимых мероприятий по диагностированию ЭО на надежность функционирования системы электроснабжения в целом.
Одним из способов предварительной оценки влияния вводимых мероприятий по диагностированию электрооборудования на надежность функционирования СЭС является проведение анализа изменения значений комплексных показателей надежности. В качестве таких показателей можно использовать коэффициент готовности (КГ) и коэффициент технического использования (КТИ).
Цель исследования
Определение функциональной зависимости выбранных показателей надежности от периодов диагностирования электрооборудования и качества проведения работ по диагностическому контролю.
Исходные предположения и допущения метода исследования
Для определения коэффициента готовности и коэффициента технического использования сложной системы, какой является СЭС, обычно учитывают только два крайних состояния системы – исправное и состояние отказа – и не анализируют процесс перехода из одного крайнего состояния в другое [5, 7]. В отличие от этой схемы, реальный процесс функционирования системы сопровождается постепенным накоплением нарушений, т.е. появлением дефектов.
В работе [2] построена полумарковская модель функционирования системы электроснабжения, которая в моменты времени, соответствующие смене состояний системы, является однородной цепью Маркова, вложенной в процесс η(t). Разработанная модель включает в себя: ориентированный граф состояний и переходов электрооборудования, матрицу вероятностных переходов, а также формулы вероятности переходов из состояния Si в состояние Sj. Схема смены состояний СЭС приведена в виде графа, изображенного на рисунке. На графе случайное время перехода из состояния в состояние обозначено греческой буквой t, а детерминированное – латинскими буквами t или Т.
Задачу отыскания коэффициента готовности (КГ) и коэффициента технического использования (КТИ) с помощью разработанной модели будем решать через определение средней доли времени пребывания процесса η (t) в каждом из состояний Si, i = 1, 2, …, 6. Напрямую из процесса η (t) найти эти характеристики не представляется возможным, поэтому для их определения будет использован метод вложенных цепей Маркова [8].
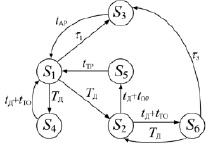
Ориентированный граф смены состояний СЭС в процессе его эксплуатации, где S1 – СЭС находится в состоянии исправной работы; S2 – ЭО диагностируется, находясь в неисправном состоянии; S3 – СЭС отказала, проводится аварийный ремонт; S4 – ЭО диагностируется, находясь в исправном состоянии; S5 – в СЭС проводится текущий ремонт; S6 – СЭС работает при наличии дефекта
Разработка модели
Практика показывает, что ЭО эксплуатируется в течение времени, значительно превосходящего период Тд его диагностирования. При таком условии формально можно рассматривать процесс его функционирования на бесконечном интервале времени. Будем считать, что нахождение ЭО в работоспособном состоянии приносит определенный доход, в этом случае качество функционирования оборудования можно измерить средним удельным доходом, который согласно [3], будет равен
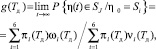 (1)
(1)
где g(Tд) – относительная доля времени, которую процесс находится в состояниях множества SJ;
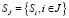 – множество состояний процесса, приносящих доход от эксплуатации ЭО;
– множество состояний процесса, приносящих доход от эксплуатации ЭО;
η0 – состояние процесса h(t) в момент времени t = 0;
πi(Tд) – финальные вероятности цепи 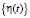 ;
;
ωi(Tд) – средний доход (полезное время) для i-го состояния;
νi(Tд) – усредненное математическое ожидание (МО) длительности одного шага процесса h(t), состоящего в переходе из Si в какое-то новое состояние Sj, j = 1, 2, …, 6.
Для вычисления величины среднего удельного дохода получим выражения для характеристик νi(Tд) и ωi(Tд).
Введем понятия, необходимые для определения νi(Tд). Переходным интервалом (переходом) 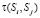 будем называть промежуток времени между моментом попадания ЭО в состояние Si и моментом попадания в Sj при следующем переходе [6]. Тогда, усредняя математическое ожидание длительности перехода из Si в Sj по всем возможным переходам, получим
будем называть промежуток времени между моментом попадания ЭО в состояние Si и моментом попадания в Sj при следующем переходе [6]. Тогда, усредняя математическое ожидание длительности перехода из Si в Sj по всем возможным переходам, получим
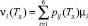 , (2)
, (2)
где 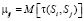 – МО длительности одного шага процесса, начинающегося в Si и заканчивающегося в Sj;
– МО длительности одного шага процесса, начинающегося в Si и заканчивающегося в Sj;
pij(Tд) – вероятность перехода из Si в Sj за один шаг.
Математическое ожидание 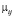 определяется выражением
определяется выражением
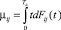 , (3)
, (3)
где Fij(Tд) – функция распределения (ФР) длительности пребывания полумарковского процесса в состоянии Si при условии последующего перехода в состояние Sj.
Подставив формулу (3) в выражение (2), получим
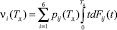 . (4)
. (4)
Перейдем к определению ωi(Tд) и ФР, входящих в νi(Tд). Если в момент времени t ЭО находится в состоянии S1 и на интервале (t, t + Tд) не произойдет отказа, то оно все время Tд будет находиться в состоянии S1. Если же произойдет отказ, то в состоянии S1 ЭО в среднем находится время t1, где t1 – МО времени, в течение которого не произошел отказ. Тогда согласно определению дохода и функции F1(t) получаем
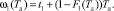 (5)
(5)
Аналогично
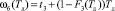 , (6)
, (6)
где t3 – МО времени, в течение которого не произойдет отказ ЭО с дефектом. Для выбранного правила диагностирования ЭО по определению дохода и множества SJ имеем:
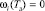 , i = 2, 3, 4, 5. (7)
, i = 2, 3, 4, 5. (7)
Так как рассматривается функционирование ЭО за один период Tд, то
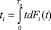 , i = 1, 3. (8)
, i = 1, 3. (8)
Формулы (5), (6) с учетом (8) принимают вид
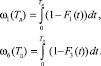 (9)
(9)
Отнесем понятие усредненной длительности перехода ЭО из состояния Si за период времени Tд к номеру состояния i. Определим время пребывания в состоянии Si до перехода в следующее состояние Sj как случайную величину t с ФР Fij(t). Для удобства можно говорить, что ЭО находится в состоянии Si, готовясь перейти в Sj. Будущее состояние процесса и переходный интервал определяются совместно с помощью двумерного распределения [1]:
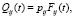 (10)
(10)
где Qij(t) выражает вероятность того, что при исходном состоянии Si процесс перейдет за один шаг в состояние Sj, время пребывания процесса в Si не превзойдет величины t, т.е.
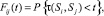
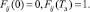 (11)
(11)
Введем в соответствии с (10) и (11) ФР длительности пребывания процесса в состоянии Si при условии его перехода в Sj на интервале времени от t до t + Tд. Выражения для определения данных ФР имеют вид
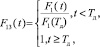 (12)
(12)
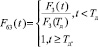 . (13)
. (13)
Так как переходы 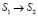 ,
, 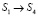 ,
, 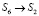 всегда происходят за постоянное время, равное периоду Tд диагностирования, то Fij(t) для этих состояний можно записать [1]:
всегда происходят за постоянное время, равное периоду Tд диагностирования, то Fij(t) для этих состояний можно записать [1]:
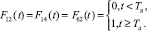 (14)
(14)
Точно так же введем ФР:
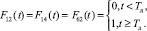 (15)
(15)
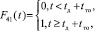 (16)
(16)
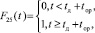 (17)
(17)
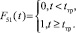 (18)
(18)
Подставляя в (4) вероятности pij(Tд) [3] и используя ФР (12), (13) для i = 1, получаем
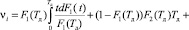
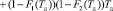 . (19)
. (19)
После преобразований (19) принимает вид
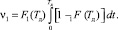 (20)
(20)
Аналогично находим
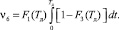 (21)
(21)
Остальные усредненные длительности переходов легко определяются из формул (14)–(18) и (4) для i = 2, 3, 4, 5:
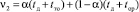 , (22)
, (22)
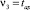 , (23)
, (23)
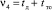 , (24)
, (24)
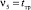 . (25)
. (25)
Теперь дадим надежностную интерпретацию среднего удельного дохода применительно к рассматриваемой нами модели функционирования ЭО. Так как под доходом (полезным временем) на рассматриваемом переходе мы условились понимать среднее время нахождения ЭО в работоспособном состоянии, поэтому обозначим через wi(Tд) получаемый средний доход для состояния Si за время Tд. Зависимость g(Tд) в формуле (1) от периода диагностирования Tд указывает на то, что рассматривается восстанавливаемое электрооборудование. При этом в зависимости от его назначения, принятого порядка его диагностирования и технического обслуживания выражение для g(Tд) может быть различным при одном и том же множестве состояний. Это связано с возможностью различного определения величины среднего дохода wi(Tд) для состояния Si, а также с определением множества состояний ЭО, которые приносят доход. Для определения g(Tд) важно также решить вопрос о порядке проведения диагностирования. Если ЭО диагностируется при его использовании по назначению, т. е. контроль при отсутствии отказа ведется параллельно с его работой, то время, в течение которого выполняется диагностирование, можно отнести в доход. Такое решение является правильным, так как здесь средний удельный доход отождествляется с надежностной характеристикой ЭО, а не с ее стоимостной единицей. Если же при выполнении диагностирования и при отсутствии отказа ЭО не используется, т.е. выводится из работы для проведения диагностических мероприятий, то время диагностирования в доход не включается.
Рассмотрим случай, когда ЭО с дефектом приносит доход до тех пор, пока не откажет, т.е. будем учитывать лишь его предрасположенность к отказам без учета снижения качества его функционирования. Перерывы в работе ЭО допускаются лишь при выполнении диагностирования и профилактических работ.
Пусть SJ – множество работоспособных состояний ЭО, приносящих доход. Тогда для рассматриваемого нами случая 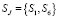 , так как доход будет приносить нахождение ЭО в исправном состоянии и в состоянии работы с дефектом. Формула (1) для модели, представленной на рисунке, принимает вид
, так как доход будет приносить нахождение ЭО в исправном состоянии и в состоянии работы с дефектом. Формула (1) для модели, представленной на рисунке, принимает вид
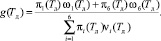 (26)
(26)
В соответствии с принятыми определениями g(Tд) выражает отношение МО времени пребывания ЭО в работоспособном состоянии за рассматриваемый период эксплуатации Tд к сумме МО времени пребывания ее в работоспособном состоянии, времени простоев, обусловленных проведением диагностирования, и временем ремонтов за тот же период. Согласно [4] g(Tд) есть коэффициент технического использования (КТИ) следовательно выражение (26) можно представить в виде
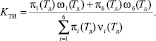 (27)
(27)
Перейдем к установлению зависимости КГ(Тд). Выразим КГ(Тд) через КТИ. Обозначим
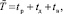 (28)
(28)
где tр, tд, tв – МО времени нахождения ЭО на интервале времени 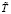 соответственно в состояниях работоспособности, диагностирования и восстановления. Тогда согласно [4]:
соответственно в состояниях работоспособности, диагностирования и восстановления. Тогда согласно [4]:
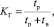 (29)
(29)
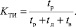 (30)
(30)
Решая совместно (29) и (30), получим
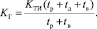 (31)
(31)
Элементарными преобразованиями приводим (31) к виду
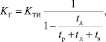 (32)
(32)
где слагаемое 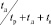 выражает долю времени, которую процесс находится в состоянии диагностирования. Тогда, повторяя рассуждения, проведенные выше, для состояния диагностирования ЭО и используя формулы (27), (32), получим
выражает долю времени, которую процесс находится в состоянии диагностирования. Тогда, повторяя рассуждения, проведенные выше, для состояния диагностирования ЭО и используя формулы (27), (32), получим
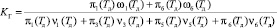 . (33)
. (33)
Результаты исследования и их обсуждение
Определены функциональные зависимости показателей надежности от периодов диагностирования электрооборудования и качества проведения работ по диагностическому контролю. С помощью выражений (27) и (33) можно определить числовые значения рассматриваемых показателей КГ и КТИ. Адекватность полученной модели подтверждается использованием апробированного математического аппарата.
Выводы
Эффективность использования средств диагностирования электрооборудования в процессе эксплуатации СЭС можно оценить, сравнив значения показателей надежности СЭС при действующей стратегии технического обслуживания и ремонта со значениями показателей надежности при введении постоянного (периодического) диагностирования ЭО. В случае повышения показателей надежности и выполнения экономического критерия можно принять положительное решение о целесообразности использования диагностического контроля.



