Актуальность исследования
В пятиуровневой системе автоматизации [1] уровень управления технологическими операциями (Control) представляется промышленными контроллерами (ПК), аналоговым или цифровым образом взаимодействующими с уровнем средств автоматического регулирования (Input/Output), в котором реализуются контурные регуляторы (КР) и технологическая автоматика с её защитами и блокировками. Косвенное управление [4] означает управление или регулирование посредством изменения настроечных параметров регуляторов, а в случае технологической автоматики – посредством изменения потока булевых переменных (рис. 1).
При организации цифрового регулирования в автоматизированной системе управления технологическими процессами (АСУТП) КР заменяют цифровыми контурными регуляторами (ЦКР) на основе коммерческих или специализированных микропроцессоров, координацию которых осуществляет ПК (уровня Control), направляя в ЦКР требуемый поток настроечных параметров в соответствующих обстоятельствах.
Если при такой организации согласованного функционирования цифровых контурных регуляторов результаты не обеспечат требуемую динамику регулирования, то ПК прерывает процесс регулирования и осуществляет переход к специальным программам защит и блокировок, отрабатывающих функции алгебры логики, временные логические функции или рекуррентные булевы функции первого и второго рода [2] для ограничения негативного воздействия нештатного функционирования регуляторов на технологические процессы и оборудование. Однако всякое прерывание процессов регулирования в связи с неподходящим функционированием регуляторов может существенно ухудшить показатели качества всей АСУТП, а переход к реализации мероприятий противоаварийного характера может и вовсе остановить соответствующие технологические процессы. Поэтому решение вопросов текущего (оперативного) корректирования (изменения) алгоритмов регулирования для достижения требуемого функционирования регуляторов представляется актуальным.
В силу специфики косвенного управления в работе предложен путь изменения алгоритмов регулирования посредством оперативной корректировки настроечных параметров в процессе регулирования.
Идея корректировки
При косвенном управлении в АСУТП традиционно ПК уровня Control координирует и взаимодействует с ЦКР нижнего уровня Input/Output как с локальными регуляторами передавая соответствующие потоки уставок и настроечных параметров (рис. 2), то есть структура взаимодействия двух уровней разделяет функции своих процессорных компонентов. Именно это разделение, по-видимому, провоцирует либо прерывание процессов регулирования при неподходящем функционировании ЦКР, либо внедрение отказоустойчивых структур регулирования при проектировании, что, безусловно, ведёт к значительному аппаратному усложнению. Чтобы избежать усложнений аппаратуры и прерывания процессов регулирования, учитывая возможность использования быстродействующих (высокопроизводительных) ПК, разделение функций ПК и ЦКР можно сделать временным или ситуационным, возложив дополнительно на ПК ведущую роль по восстановлению требуемой динамики регулирования в цепях ЦКР и оградив тем самым уровень Input/Output от возможной потери устойчивости регуляторами.
При оценке возможности потери устойчивости ЦКР ввиду не предполагаемых влияний среды ПК осуществляет его «захват» и управляющая программа ПК организует временный вычислительный комплекс «ПК – ЦКР» (с единой операционной системой) до момента восстановления требуемого функционирования. А восстановление требуемого функционирования ЦКР может быть проведено как поиск настроечных параметров и моделирование в ПК работы цепи регулирования с этими параметрами.
Тогда методика косвенного цифрового управления может быть представлена в следующем порядке:
1. Задание серий значений настроечных параметров:
1.1) задание значений коэффициента усиления пропорциональной составляющей:  ,
, 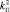 , …,
, …, 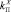 ;
;
1.2) задание значений коэффициента усиления интегрирующей составляющей: 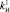 ,
, 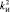 , …,
, …, 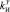 ;
;
1.3) задание значений коэффициента усиления дифференцирующей составляющей: 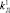 ,
, 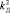 , …,
, …, 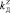 .
.
2. Моделирование для каждой модели ПИД-регулятора значения управляющего воздействия: 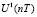 для
для 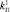 ,
, 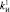 и
и 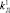 ;
; 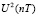 для
для 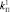 ,
, 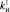 и
и 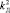 ; …;
; …; 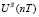 для
для 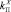 ,
, 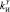 и
и 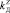
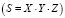 .
.
3. Верификация управляющего воздействия и выбор лучшего варианта закона регулирования:
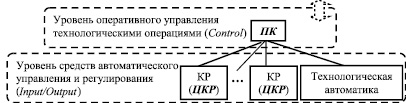
Рис. 1. Нижние уровни системы автоматизации при косвенном управлении, где: ПК – промышленный контроллер; КР – контурный регулятор; ЦКР – цифровой контурный регулятор
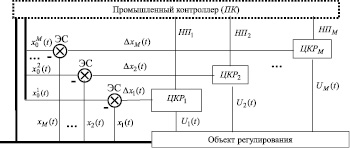
Рис. 2. Пример схематического взаимодействия уровней Control (ПК) и Input/Output (цифровые контурные регуляторы ЦКР1, ЦКР2, …, ЦКРМ) системы автоматизации промышленного предприятия, где: 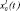 ,
, 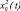 , …,
, …, 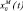 – задающие воздействия соответственно для ЦКР1, ЦКР2, …, ЦКРМ; х1(t), х2(t), …, ΔxM(t) – регулируемые величины; Δx1(t), Δx2(t), …, ΔxM(t) – рассогласования (отклонения, ошибки) в текущий момент, пропорциональные соответственно
– задающие воздействия соответственно для ЦКР1, ЦКР2, …, ЦКРМ; х1(t), х2(t), …, ΔxM(t) – регулируемые величины; Δx1(t), Δx2(t), …, ΔxM(t) – рассогласования (отклонения, ошибки) в текущий момент, пропорциональные соответственно 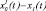 ,
, 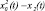 , …,
, …, 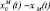 ;
; 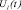 ,
, 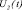 , …,
, …, 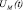 – управляющие воздействия, рассчитанные соответственно регуляторами ЦКР1, ЦКР2, …, ЦКРМ; НП1, НП2, …, НПМ – настроечные параметры соответственно для ЦКР1, ЦКР2, …, ЦКРМ;
– управляющие воздействия, рассчитанные соответственно регуляторами ЦКР1, ЦКР2, …, ЦКРМ; НП1, НП2, …, НПМ – настроечные параметры соответственно для ЦКР1, ЦКР2, …, ЦКРМ; 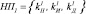 ,
, 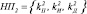 , …,
, …, 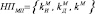 ; ЭС – элемент сравнения; утолщенная линия – шина, по которой осуществляется взаимодействие уровней
; ЭС – элемент сравнения; утолщенная линия – шина, по которой осуществляется взаимодействие уровней
3.1. Моделирование реакции объекта управления в момент времени 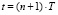 на соответствующее управляющее воздействие:
на соответствующее управляющее воздействие: 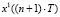 для
для 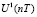 ,
, 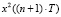 для
для 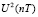 , …,
, …, 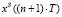 для
для 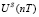 .
.
3.2. Вычисление рассогласований в момент времени 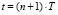 :
: 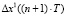 для
для 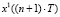 ,
, 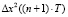 для
для 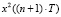 , …,
, …, 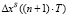 для
для 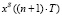 .
.
3.3. Поиск минимального рассогласования:
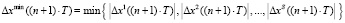 .
.
3.4. Выбор настроечных параметров для вычисления управляющего воздействия цифрового ПИД-регулятора:
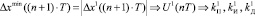 ;
;
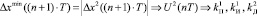 ; …;
; …;
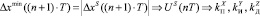 .
.
Алгоритм косвенного управления для классической итерационной модели цифрового ПИД-регулирования
Классическая итерационная формула расчета управляющего воздействия цифрового ПИД-регулятора (формула прямоугольника), предложенная профессором В.И. Мазуровым [3], имеет вид
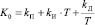 ,
, 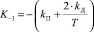 ,
,
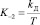 , (1)
, (1)
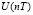 =
= 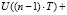
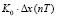 +
+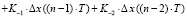 . (2)
. (2)
В качестве модели объекта управления в алгоритме используем модель токового контура двигателя постоянного тока:
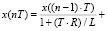
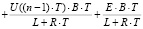 , (3)
, (3)
где R – сопротивление обмотки якоря; L – индуктивность цепи якоря; B – коэффициент передачи датчика тока; E – ЭДС самоиндукции.
Алгоритм корректировки настроечных параметров цифровых регуляторов для формулы прямоугольника по предложенной методике косвенного цифрового управления сводится к реализации мероприятий:
1. Задание значений настроечных параметров:
1.1) задание значений коэффициента усиления пропорциональной составляющей, например 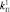 ,
, 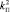 ,
, 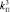 ;
;
1.2) задание значений коэффициента усиления интегрирующей составляющей, например 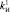 ,
, 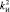 ,
, 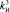 ;
;
1.3) задание значений коэффициента усиления дифференцирующей составляющей, например 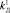 ,
, 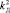 ,
, 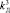 .
.
2. Моделирование по каждой модели ПИД-регулятора значения управляющего воздействия по формулам (1) и (2):
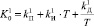 ,
, 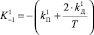 ,
,
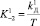 ,
,
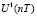 =
= 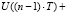
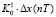 +
+
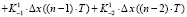 ;
;
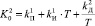 ,
, 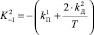 ,
,
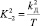 ,
,
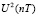 =
= 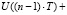
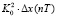 +
+
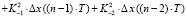 ; …;
; …;
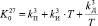 ,
, 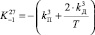 ,
,
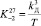 ,
,
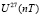 =
= 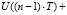
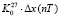 +
+
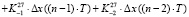 .
.
3. Верификация управляющего воздействия и выбор лучшего варианта закона регулирования:
3.1. Моделирование реакции объекта управления в момент времени 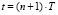 на соответствующее управляющее воздействие по математической модели (3):
на соответствующее управляющее воздействие по математической модели (3):
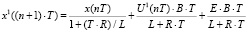 ,
,
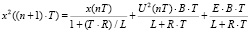 , …,
, …,
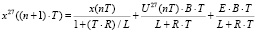 .
.
3.2. Вычисление рассогласований в момент времени 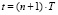 :
:
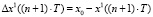 ,
, 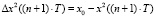 , …,
, …,
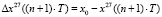 .
.
3.3. Поиск минимального рассогласования:
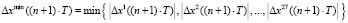 .
.
3.4. Выбор настроечных параметров для вычисления управляющего воздействия цифрового ПИД-регулятора:
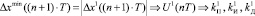 ;
;
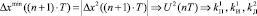 ; …,
; …,
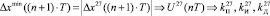 .
.
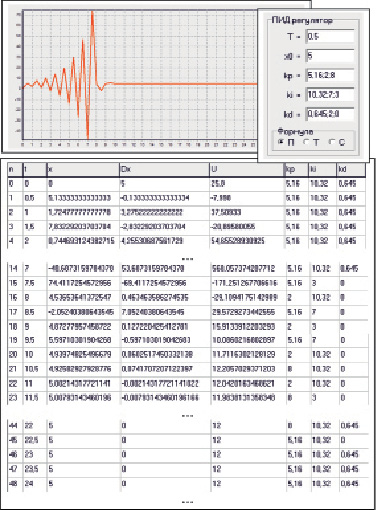
Рис. 3. Моделирование алгоритма косвенного управления для серий настроечных параметров 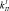 = 5,16,
= 5,16, 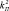 = 2,
= 2, 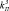 = 8,
= 8, 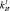 = 10,32,
= 10,32, 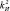 = 7,
= 7, 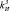 = 3,
= 3, 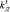 = 0,645,
= 0,645, 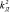 = 2,
= 2, 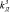 = 2, модели регулятора (1)–(2) и модели объекта управления (3)
= 2, модели регулятора (1)–(2) и модели объекта управления (3)
Моделирование предложенного алгоритма косвенного управления для настроечных параметров 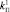 = 5,16,
= 5,16, 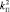 = 2,
= 2, 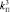 = 8,
= 8, 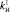 = 10,32,
= 10,32, 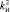 = 7,
= 7, 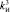 = 3,
= 3, 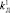 = 0,645,
= 0,645, 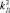 = 2,
= 2, 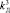 = 2 продемонстрировано на рис. 3. Цифровой ПИД регулятор уровня Input/Output настроен на настроечные параметры kП = 5,16, kИ = 10,32 и kД = 0,645, рассчитанные методом Зиглера – Николса [5]. Моделирование показывает расходящуюся динамику регулируемого параметра с выбранными настроечными параметрами. Начиная с t = 7,5 моделируется захват цифрового ПИД-регулятора промышленным контроллером уровня Control и отработка предложенного алгоритма промышленным контроллером. Начиная с t = 23 ПИД-регулятор уровня Input/Output отрабатывает требуемую динамику регулируемого параметра на изначально заданных настроечных параметрах в связи с чем происходит отключение косвенного управления (рис. 3).
= 2 продемонстрировано на рис. 3. Цифровой ПИД регулятор уровня Input/Output настроен на настроечные параметры kП = 5,16, kИ = 10,32 и kД = 0,645, рассчитанные методом Зиглера – Николса [5]. Моделирование показывает расходящуюся динамику регулируемого параметра с выбранными настроечными параметрами. Начиная с t = 7,5 моделируется захват цифрового ПИД-регулятора промышленным контроллером уровня Control и отработка предложенного алгоритма промышленным контроллером. Начиная с t = 23 ПИД-регулятор уровня Input/Output отрабатывает требуемую динамику регулируемого параметра на изначально заданных настроечных параметрах в связи с чем происходит отключение косвенного управления (рис. 3).
Выводы
Модельные эксперименты предложенного процесса корректировки настроечных параметров показали продуктивность использования идеи изменения алгоритмов регулирования посредством оперативной корректировки настроечных параметров в процессе регулирования.
Исследование выполнено при поддержке ОГУ имени И.С. Тургенева по теме «Разработка программной системы поддержки процесса управления в предаварийных состояниях для восстановления нормальной работы», приказ № 7-н/26 от 23.10.2013 г.



