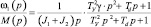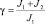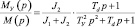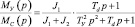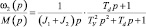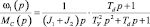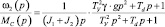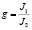В технической литературе имеются ряд рекомендаций по настройке параметров регуляторов в системах электропривода с учетом упругих связей [1, 3, 4]. Но эти методики, как правило, излишне усложнены и не получили распространения в инженерной практике. Ниже приводятся достаточно наглядные и простые инженерные методы синтеза параметров регуляторов в системах электропривода с учетом упругих связей [5].
Структурная схема двухмассовой упруго-вязкой механической системы хорошо известна (рис. 1).
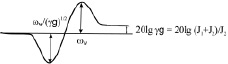
В данной структуре два входных воздействия (М, Мс) и три выходных координаты (w1, w2, Му ). Передаточные функции для этой структуры сведены в табл. 1. В таблице приведены также ЛАЧХ той части передаточной функции, которая отражает влияние упругости.
Во всех передаточных функциях в знаменателе один полином второго порядка, отражающий влияние упругости
,
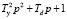где
= 
,
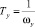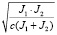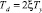(ξ – коэффициент затухания).
Комплексные корни полинома:
.
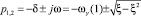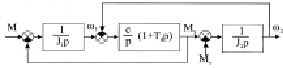
Рис. 1. Структурная схема двухмассовой упруго-вязкой механической системы
Таблица 1
Математическое описание двухмассовой механической системы
|
Передаточная функция |
Частотные характеристики звеньев, учитывающие влияние упругости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В подобных системах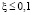 
, поэтому 
.
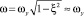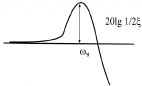
Амплитуда резонансного пика колебательного звена
.
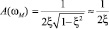Как влияют упруго-вязкая система и САР скорости друг на друга?
Возможны три случая:
1) 
;
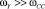2) 
;
3) 
,
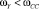где ωсс – частота среза оптимизированного контура скорости, оптимизированного на МО или СО.
В первом случае влиянием упругости при расчете параметров регуляторов можно пренебречь.
Во втором и третьем случаях синтез регулятора скорости следует вести с учетом влияния упругости.
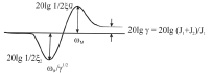
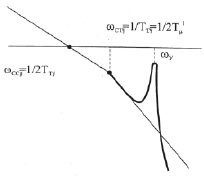
Предлагается следующее правило настройки для 2-го случая (ωY ≈ ωCC): Резонансный пик ЛАЧХ разомкнутой САР скорости с учетом влияния упругости должен лежать ниже оси абсцисс не менее чем на 6 дб (рис. 2).
Если резонансный пик пересекает ось абсцисс, система становится неустойчивой (САР скорости входит в режим автоколебаний).
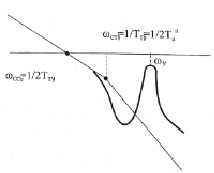
На рис. 2 представлены ЛАЧХ разомкнутой системы при обратной связи по скорости механизма или двигателя с учетом упругой связи. Причем частота среза контура скорости ωCC и контура тока wСТУ снижены с тем, чтобы обеспечить на частоте ωY опускание резонансного пика ниже оси абсцисс на 6 дб. Соотношение между частотами среза контура тока и контура скорости остается неизменной – (ωСТУ/ωССУ = 2).
Новые малые постоянные времени с учетом влияния упругости для расчета параметров контура тока и скорости в этом случае равны:
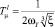(о.с. по w2),
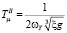(о.с. по w1).
Новые частоты среза контуров тока и скорости в этих условиях равны:
o.с. по w2 :
;
;
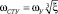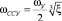o.с. по w1 :
;
.
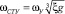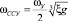а)
б)
Рис. 2. ЛАЧХ разомкнутой САР скорости с учетом упруго-вязкой системы: а) при о.с. по скорости механизма; б) при о.с. по скорости двигателя
Из выражений для частоты среза контура скорости следует, что при g > 1 (при моменте инерции двигателя меньше, чем приведенный момент инерции механизма) при о.с., по скорости механизма можно получить большее быстродействие, чем при о.с. по скорости двигателя.
Но всегда частота среза контура скорости получается меньше частоты упругих колебаний. В этом случае можно говорить о слабой электромеханической связи [3]. Быстродействие контуров скорости и тока приходится снижать, чтобы система электропривода была устойчивой и влияние упругости на контуры слабо сказывалось. Физически это означает, что механические колебания не развиваются от воздействия момента двигателя. Но колебания, могущие возникнуть от воздействия статического момента, слабо демпфируются системой электропривода.
Рассмотрим третий случай – ωУ < ωCC
При обратной связи по скорости механизма настройка производится по тем же правилам, что и во втором случае (резонансный пик на ЛАЧХ должен быть ниже оси абсцисс на 6 дб). Реальную частоту среза приходится снижать по условиям устойчивости. Всегда ωссу < ωCC. Демпфирование колебаний от статического момента со стороны электропривода незначительно.
В случае обратной связи по скорости двигателя при q > 1 оказывается возможным увеличить демпфирующую способность электропривода. Настройку параметров регуляторов следует вести по корням характеристического полинома.
В подобной системе можно пренебречь малой постоянной времени Тст скоростного контура и внутренним демпфированием Тd в механической системе. Тогда из первоначальной передаточной функции разомкнутого контура скорости при П-РС получаем
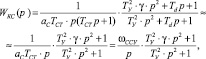
где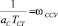 
– новая частота среза контура скорости с учетом упругости.
Тогда передаточная функция замкнутого контура скорости
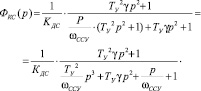
Исследуем характеристический полином
.
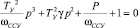При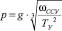 
получим
.
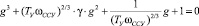Имеем нормализованный вид характеристического полинома
,
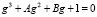где
;
; 
.
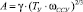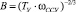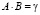По диаграмме Вышнеградского для характеристического полинома 3-го порядка можно выбрать коэффициенты А и В в зависимости от величины γ. Практика настроек показывает, что наиболее рационально принять А = В. Тогда получается частота среза
.
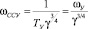Уже при γ > 1,5 можно получить ξ = 0,2÷0,3. При γ = 4 ξ = 0,5.
При γ > 9 получаются апериодические переходные процессы. Так как γ > 1, то ωССУ всегда меньше ωУ, как и в предыдущих настройках.
Настройка позволяет выбрать такую частоту среза контура скорости, при которой обеспечивается наилучшее демпфирование упругих колебаний за счет замкнутого контура скорости.
Если оставить ωСС >> ωУ (не уменьшать частоту среза контура скорости), получаем так называемую «жесткую» электромеханическую связь. Скорость двигателя будет изменяться в соответствии с заданием и не имеет практически колебаний. Масса механизма находится в режиме слабо затухающих колебаний по отношению к массе двигателя (при независимости статического момента от скорости).
Учитывая рост полосы пропускания современных электроприводов наилучшее демпфирование упругих колебаний за счет электропривода вполне достижимо. Пример такого решения приведен в [2].
Рассмотрим колебания упругого момента при переходных процессах по заданию скорости в системе электропривода. Если принять, что время нарастания момента (тока) двигателя равно Т (рис. 18.2), то коэффициент динамичности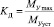 
будет зависеть от соотношения 
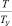(рис. 3).
Чтобы ограничить динамические перегрузки в механических передачах, нужно обеспечить KД на уровне 1,2÷1,4. Для этого необходимо обеспечить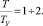 
Время первого согласования в контуре тока, настроенном на МО, равно 4,7 ТМ. Поэтому малая постоянная токового контура, выбранная из условия минимизации динамических усилий в передачах, должна быть
.
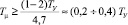Настройки параметров регуляторов тока и скорости, рекомендуемые выше, обеспечивают данное условие.
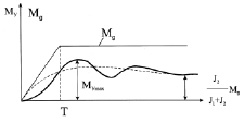
Рис. 3. Переходная характеристика упругого момента в передаче при линейном нарастании момента двигателя Мд
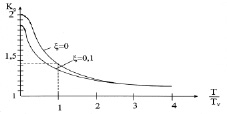
Рис. 4. Зависимость коэффициента динамичности КД от соотношения Т/ ТУ
Чтобы ограничить динамические перегрузки в механической части производственного механизма при воздействии статического момента, следует также по возможности ограничивать темп нарастания нагрузки на валу механизма.