В настоящее время наблюдается интенсивное развитие применения нечеткой логики для целей управления. Увеличение практического применения нечетких методов управления главным образом было обусловлено ростом сложности математических моделей реальных объектов, при которых применение традиционных методов построения моделей уже не приводило к удовлетворительным результатам. В большинстве случаев технология нечеткого моделирования применяется для синтеза систем управления при недостаточной информации об объекте управления, неточном и неполном описании решаемой проблемы, поскольку не требует для синтеза регуляторов модели объектов управления. Однако и при наличии модели объекта управления применение нечеткой логики является весьма продуктивным, в частности при проектировании нестационарных систем управления. Во многих видах систем управления необходимо уделять особое внимание различным режимам работы. В таких системах для автоматизации удобно использовать нечеткое управление, поскольку можно использовать однотипные правила для каждого режима.
Реальные технические объекты обладают изменяющимися во времени параметрами, т.е. являются нестационарными. Решение задач управления такими объектами требует построения нестационарных систем управления, а значит, и проектирования динамических регуляторов. В качестве корректирующих устройств в системах автоматического управления (САУ) наиболее часто используемыми на практике являются ПИД-регуляторы. Настоящая статья посвящена исследованию применения классических и нечетких ПИД-регуляторов в нестационарных системах управления.
Рассмотрим математическое описание нестационарной САУ с цифровым регулятором. Схема системы управления приведена на рис. 1. Нестационарный объект управления описывается линейными дифференциальными уравнениями, коэффициенты которых являются функциями времени.
Переменность коэффициентов дифференциальных уравнений, описывающих поведение систем автоматического управления, порождается многими факторами, а именно:
– физическими процессами, протекающими в элементах систем;
– линеаризацией нелинейных систем около опорных траекторий;
– статистической линеаризацией при подаче на вход нестационарных сигналов [5].
Рассмотрим синтез классического и нечеткого ПИД-регуляторов для нестационарного объекта, представленного фильтром второго порядка (колебательным звеном) [2]. Параметрическая передаточная функция выбранного нестационарного объекта управления в нулевом приближении:
,
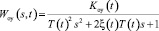где Kоу (t) – коэффициент передачи объекта управления, T – постоянная времени, ξ – коэффициент демпфирования.
Зависимость параметров объекта управления от времени представим следующими выражениями:
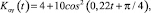
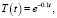
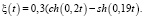
Для приводов характерны ограничения по величине вырабатываемого сигнала, поэтому в упрощенном виде он может быть представлен нелинейной зависимостью типа «насыщение» или в линеаризованном виде передаточной функцией интегрирующего звена:
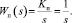
Применив для нестационарных параметров объекта разложение в ряд Тейлора передаточную функцию обобщенного объекта управления запишем в следующем виде:
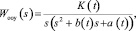
где
,
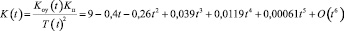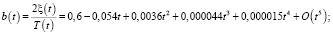
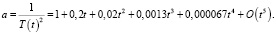
Задающее воздействие представим функцией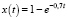 
.
Передаточная функция классическогоцифрового ПИД-регулятора:
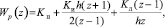
где Kп, Kи, Kд – коэффициенты пропорциональной, интегральной и дифференциальной составляющих соответственно, h – шаг квантования.
p>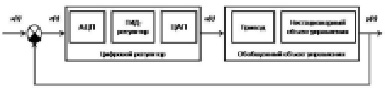
Рис. 1.Обобщенная схема нестационарной САУ с цифровым регулятором
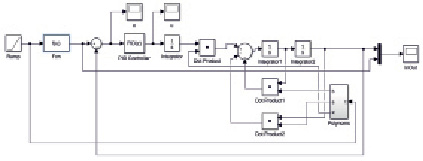
Рис. 2. Структурная схема САУ с цифровым ПИД-регулятором
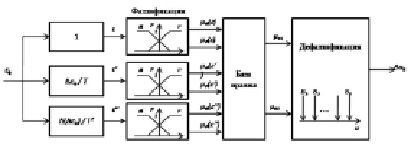
Рис. 3. Обобщенная структура нечеткой части регулятора
Структурная схема для исследования одноконтурной системы с классическим цифровым ПИД-регулятором с использованием MATLAB/SIMULINK представлена на рис. 2. После настройки параметров регулятора на шаге дискретизации h = 0,0001, получены следующие коэффициенты Kп = 1,61, Kи = 36,58, Kд = 6,68.
Рассмотрим построение для описанного объекта нечеткого ПИД-регулятора. Отличие ПИД-регулятора с контроллером, основанным на нечеткой логике, от классического заключается в том, что коэффициенты усиления в пропорциональной, интегрирующей и дифференцирующих цепях регулятора не являются статическими, т.е. зависят от состояния системы в текущий момент времени. Это позволяет сделать процесс управления более адаптивным. При построении нечетких ПИД-регуляторов чаще всего используются методики прямого или инкрементного регулирования [4]. В варианте прямого регулирования на каждом шаге дискретизации вычисляется значение управляющего сигнала uk, в инкрементном варианте – только величина приращения управляющего сигнала Δuk. Для реализации модели выбран инкрементный вариант.
Структура нечеткой части регулятора показана на рис. 3. Статическая часть нечеткого регулятора включает блок фаззификации, блок формирования логического решения (правил) и блок дефаззификации. В приведенной схеме в качестве входных параметров системы нечеткого вывода использованы три лингвистические переменные: ошибка системы, а также ее первая и вторая производные. В качестве выходной переменной выбран сигнал управления (управляющее воздействие). Для фаззификации каждого из входных сигналов выбраны два нечетких терм-множества N (Negative) и P (Positive), что обеспечивает простейшую структуру регулятора [1]. В этом случае полная база правил будет состоять из восьми элементов вида «если – то».
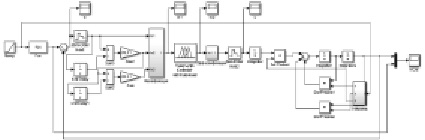
Рис. 4. Структурная схема САУ с нечетким ПИД-регулятором
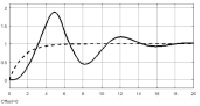
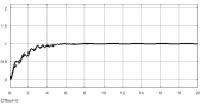
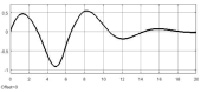
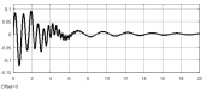
Рис. 5. Процессы в системах управления с цифровым классическим ПИД-регулятором (левый столбец) и нечетким регулятором (правый столбец)
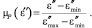
Функции принадлежности лингвистических переменных выражены в виде
; 
;
; 
;
; 
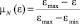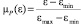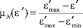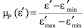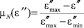Функции принадлежности управляющего воздействия:
,
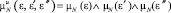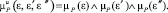
В качестве схемы нечеткого вывода применяется алгоритм Мамдани, методом активации для которого являетя min. В логическом выводе min функция принадлежности вывода отсекается по высоте, соответствующей степени истинности правила, формируя тем самым нечеткие подмножества. Полученные нечеткие подмножества объединяются вместе для формирования результирующей функции принадлежности для управляющего воздействия. В качестве метода агрегирования используется операция mах-дизъюнкции, при которой результирующее нечеткое подмножество конструируется как поточечный максимум по всем нечетким полученным подмножествам.
Функция принадлежности управляющего воздействия нечеткому множеству N ограничена сверху значением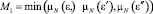 
. Функция принадлежности управляющего воздействия нечеткому множеству P ограничена сверху значением 
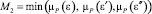. Результирующая функция принадлежности получается формированием максимума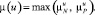 
В блоке дефаззификации полученная результирующая функция принадлежности преобразуется в числовую величину. Для определения конкретного значения приращения управляющего воздействия воспользуемся методом определения абсциссы «центра тяжести» фигуры, образованной результирующей функцией принадлежности [3]:
,
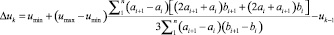где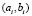 
– координаты точек результирующей фигуры.
Система, реализующая нечеткий ПИД-регулятор, разработана при помощи приложения MATLAB/FUZZY LOGIC TOOLBOX и представлена на рис. 4. Нечеткий регулятор в системе управления состоит из аналого-цифрового преобразователя АЦП, представленного фиксатором Zero-Order Hold, блоков оценки первой и второй производных ошибки системы, блоков нормировки входных (normin) и выходного (normout) сигналов, центрального блока нечеткого регулятора Fuzzy Logic Controller и выходного цифроаналогового преобразователя, представленного фиксатором Zero-Order Hold 1. В центральном блоке нечеткого регулятора Fuzzy Logic Controller задаются функции принадлежности базы правил. В редакторе функций принадлежности присутствуют одиннадцать типовых форм функций, из которых в системах управления наиболее целесообразно использовать пары симметричных друг относительно друга треугольных, колоколообразных, гауссовых и экспоненциальных функций [6]. В работе использованы треугольные функции принадлежности для входов и выхода fuzzy-регулятора.
На рис. 5 представлены результаты моделирования поведения системы управления. На рисунке приведены процессы в системах управления: слева – в системе с настроенным цифровым ПИД-регулятором; справа – в системе с настроенным нечетким регулятором.
Приведенные характеристики подтверждают эффективность применения нечетких ПИД-подобных регуляторов для управления нестационарными объектами. Анализируя характеристики процессов, можно заключить, что как классический ПИД-регулятор, так и нечеткий регулятор в системе управления обеспечивают устойчивое слежение с достаточно малыми ошибками рассогласования, при этом система с нечетким регулятором обеспечивает ошибку рассогласования почти на порядок меньше, чем ошибка рассогласования в системе с классическим ПИД-регулятором. При недостаточной точности управления целесообразно увеличить количество терм-множеств, используемых при синтезе нечеткого регулятора, при увеличении диапазона изменения параметров нестационарных объектов – применение многоканальных нечетких регуляторов, где каждый канал настроен на определенный участок диапазона изменения параметров объекта.