Термодинамика процесса дегидроксилации слюд
На основании анализа литературных и собственных экспериментальных данных можно полагать, что при нагревании природной слюды в ее составе происходят изменения, связанные с удалением из межслоевого пространства не только молекулярной воды (дегидратация), но и гидроксильных ионов (дегидроксилация) [10, 14]. Суммарный процесс удаления различных форм воды можно представить совокупностью отдельных стадий. Для мусковита такими стадиями являются:
1. Стадия удаления молекулярной воды
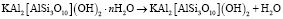 (1)
(1)
гидрослюда слюда
2. Стадия удаления конституционной воды
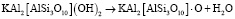 (2)
(2)
слюда дегидроксилат
Совершенно очевидно, что равновесие между гидратированной слюдой и слюдой (уравнение 1) определяется закономерностями сорбционных явлений, детальные аспекты которых для минеральных слоистых материалов рассмотрены в специальной литературе [2]. В связи с этим отметим лишь следующие положения.
Известно [2], что скорость адсорбции ωαqcc определяется величиной давления (Р) и степенью заполнения поверхности сорбируемым веществом Q, т.е.
Qaqc = k1(1 – Q)P, (3)
где Q – степень заполнения поверхности в долях единицы.
Скорость десорбции воды ωqec прямо пропорциональная степени заполнения, т.е.
ωqec = k1Q, (4)
где k1 и k2 – константы скорости процесса сорбции и десорбции воды соответственно.
В условиях равновесия, которые рассматривает термодинамика, скорости этих двух взаимопротивоположных процессов становятся одинаковыми, т.е.
ωαqc = ωqec. (5)
Тогда на основании уравнений (3) и (4) имеем
k1(1 – Q)P = k2Q. (6)
Следовательно,
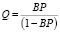 , (7)
, (7)
где В – новая переменная величина, равная
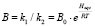 , (8)
, (8)
Haqc – теплота адсорбции молекулярной воды поверхностью слюды;
B0 – постоянная для данной температуры.
Процесс дегидроксилации соответствует уравнению (2), из которого следует, что константа равновесия между фазой мусковита и его безводной формой – дегидроксилатом определяется только величиной парциального давления паров воды
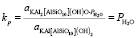 , (9)
, (9)
где kp – константа равновесия реакции (2); 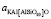 – активность дегидроксилата;
– активность дегидроксилата; 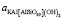 – активность слюды;
– активность слюды; 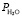 – парциальное давление воды.
– парциальное давление воды.
Положение равновесия реакции (2) характеризуется величиной константы равновесия (уравнение (9) и зависит от температуры (уравнение Вант-Гоффа):
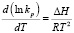 , (10)
, (10)
где kp – константа равновесия; ΔH – энтальпия реакции; R – универсальная газовая постоянная. Таким образом, количество гидроксилата, как и количество воды, образующейся из гидроксильных ионов, входящих в структуру алюмо-кремниевых тетраэдров, также является функцией температуры.
Из уравнения (9) и (10) следует, что:
1. Рассматриваемая система при постоянной температуре является моновариантной. Это значит, что каждой данной температуре соответствует одно определенное значение равновесного давления.
2. Чем ниже величина парциального давления паров воды и чем выше температуры процесса, тем полнее будет протекать реакция.
3. Молекулярная вода сохраняется в межслоевом пространстве слюды до тех пор, пока сохраняется неразложившаяся слюда. Это значит, что межслоевая вода удаляется во всем процессе дегидроксилации, однако ее количество зависит от температуры.
4. О положении равновесия реакции (2) о количестве образовавшейся воды и дегидроксилата можно судить по величине константы равновесия.
5. Парциальное давление воды и его изменение во времени может служить одним из контролируемых параметров при изучении кинетики процесса дегидроксилации.
Для оценки положения равновесия реакции (2) необходимо определить функциональную зависимость константы равновесия от температуры k(T). Константа равновесия химической реакции K связана с изменением свободной энергии Гиббса ΔG: ΔG = – RT?nk. Энергия Гиббса – функция состояния термодинамической системы, равная разности между энтальпией и произведением температуры на энтропию.
G = H – TS = A + PV.
По определению, энергия Гиббса (или потенциал Гиббса, или термодинамический потенциал) равна
G = U + PV – TS,
где U – внутренняя энергия, P – давление, V – объем, T – абсолютная температура, S – энтропия. Термодинамический потенциал Гиббса – G определяет полную химическую энергию системы. Дифференциал энергии Гиббса для системы с постоянным числом частиц:
dG = VdP – SdT.
Отсюда следует, что при = ConstΔG = ΔH – TΔS.
В химических процессах одновременно действуют два противоположных фактора – энтропийный (TΔS) и энтальпийный (ΔH). Суммарный эффект этих противоположных факторов в процессах, протекающих при постоянном давлении и температуре, определяет изменение энергии Гиббса (G):
ΔG = ΔH – TΔS.
Убыль энергии Гиббса в равновесном процессе, протекающем при P, T = Const, равна максимальной полезной работе, произведенной системой. Из обобщенного уравнения первого и второго начал термодинамики следует неравенство
TdS ≥ dU + PdV,тогда для постоянных P и T: d(U + PV –TS) ≤ 0 или d(G) ≤ 0.
Важно, что величина ΔG является критерием направленности самопроизвольного процесса в закрытой системе при P, T = Const. При ΔG < 0 процесс идет в прямом направлении, при ΔG > 0 – в обратном, при ΔG = 0 реализуется состояние равновесия.
Таким образом, для реакции дегидроксилации справедливо соотношение:
ΔG = ΔH – TΔS, (11)
где ΔG – изменение энергии Гиббса в процессе дегидроксилации, ΔH – изменение энтальпии этого процесса, ΔS – изменение энтропии, T – термодинамическая температура.
Термодинамические характеристики дегдроксилата можно оценить по известным характеристикам микроклина и корунда, на которые он разлагается и для которых они приводятся в соответствующей литературе [1, 3, 4]. Найденные таким образом значения гидроксилатов являются очевидно максимально допустимыми. Поэтому в качестве исходных данных приняты соответствующие значения (табл. 1).
Таблица 1
Исходные термодинамические характеристики [1, 7, 8]
|
Вещество |
ΔG ° кДж/моль |
ΔН ° кДж/моль |
?S ° Дж/моль град |
|
Мусковит |
– 5586 |
– 5963,7 |
296,5 |
|
Микроклин |
– 3733,6 |
– 3958,2 |
213,7 |
|
Флогопит |
– 5826,3 |
– 6209,6 |
318,9 |
|
Санидин |
– 3730,9 |
– 3950,1 |
232,2 |
|
Корунд |
– 1578,5 |
– 1670,3 |
50,8 |
|
Дегидроксилат мусковита |
– 5312 |
– 5629,9 |
264,5 |
|
Дегидроксилат флогопита |
– 5646,3 |
– 5758,4 |
375 |
|
Периклаз |
– 567,9 |
– 601,3 |
26,9 |
|
Вода |
– 228 |
– 241,2 |
188,3 |
|
Каолинит |
– 3796,7 |
– 4090,5 |
203,1 |
|
Силлиманит |
– 2440,2 |
– 2583,2 |
95,7 |
|
Кварц |
– 848,1 |
– 898,7 |
46,8 |
|
Калисилит |
– 2018,9 |
– 2106,7 |
133,1 |
|
Лейцит |
– 2654,3 |
– 3013,8 |
200 |
|
Шпинель |
– 2187,8 |
– 3954,3 |
80,5 |
|
Серпентин |
– 8071,1 |
– 8719,5 |
441,4 |
|
Энстатит |
– 1466,3 |
– 1567,5 |
67,8 |
|
Оливин |
– 2051,4 |
– 2169,4 |
95,1 |
Для реакции дегидроксилации мусковита (уравнение 2) имеем
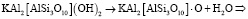
Мусковит Дегидроксилат мусковита Вода
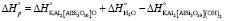
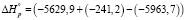 кДж/моль = 92,5 кДЖ/моль
кДж/моль = 92,5 кДЖ/моль
или
ΔН ° = 92,5 кДЖ/моль. (12)
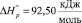
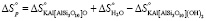
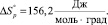 (13)
(13)
Используя уравнение (11), определяем величину энергии Гиббса процесса дегидроксилации мусковита при интересующей температуре. Результаты расчетов представлены в табл. 2.
Таблица 2
Температурная зависимость константы равновесия реакции дегидроксилации мусковита
|
T, °K |
ΔG, кДж/моль |
kp |
|
|
298 |
46,44 |
– 8,14 |
– |
|
373 |
34,78 |
– 4,88 |
– |
|
473 |
19,35 |
– 0,14 |
– |
|
573 |
3,89 |
– 0,35 |
– |
|
673 |
– 11,58 |
0,90 |
7,91 |
|
773 |
– 27,04 |
1,83 |
67,30 |
|
873 |
– 42,51 |
2,55 |
351,56 |
|
973 |
– 57,98 |
3,12 |
1303,16 |
|
1073 |
– 73,86 |
3,58 |
3784,43 |
|
1173 |
– 88,90 |
3,96 |
9162,20 |
|
1273 |
– 104,37 |
4,29 |
19319,68 |
Результаты термодинамических расчетов (табл. 2) достаточно хорошо согласуются с экспериментальными данными авторов [5, 6, 13], изучавших разложение мусковита при повышенных температурах. Полученные данные свидетельствуют о том, что дигидроксилация мусковита начинается при температуре, превышающей 400 °C. В результате дальнейшего повышения температуры степень дегидратации очень быстро растет. Это значит, что нагревание слюды до 400 °С приводит лишь к удалению молекулярной воды, в том числе и сорбированной, в то время как химически связанная вода, представленная гидроксильными ионами, остается в мусковите практически в неизменном виде.
Тот факт, что каждому значению температуры соответствует вполне определенная равновесная величина парциального давления воды, дает основание утверждать, что любые факторы, приводящие к понижению парциального давления паров воды, будут неизбежно вызывать снижение температуры гидроксилации мусковита.
Аналогичные расчеты дегидроксилации флогопита по уравнению
Флогопит Дегидроксилат флогопита Вода
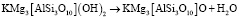 (14)
(14)
приводят к следующим результатам:
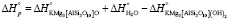
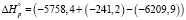 кДж/моль = 209,96 кДЖ/моль
кДж/моль = 209,96 кДЖ/моль
или
ΔН ° = 209,96 кДЖ/моль. (15)
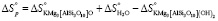 , (16)
, (16)
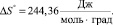
Сравнивая полученные данные по дегидроксилации флогопита с данными для мусковита, становится ясным, что флогопит является более высокотемпературным минералом. Его заметная дегидроксилация происходит примерно на 180–220 °С выше, чем дегидроксилация мусковита, что согласуется с экспериментальными данными других авторов [5, 9–12], включая данные ЯМР.
Таким образом, результаты термодинамических расчетов позволяют сделать следующие выводы:
1. Определены условия дегидроксилации флогопита и мусковита при повышенных температурах.
2. Показано, что процесс дегидроксилации флогопита происходит при температуре на 180–220 °С выше, чем у московита. Результаты термодинамических процессов согласуются с экспериментальными данными (табл. 3).
Таблица 3
Температурная зависимость константы равновесия реакции дегидроксилации флогопита
|
T, °K |
ΔG, кДж/моль |
lg kp |
|
|
298 |
137,73 |
– 24,15 |
– |
|
373 |
119,55 |
– 16,76 |
– |
|
473 |
96,30 |
– 10,53 |
– |
|
573 |
71,02 |
– 6,48 |
– |
|
673 |
46,82 |
– 3,64 |
– |
|
773 |
22,57 |
– 1,51 |
– |
|
873 |
– 1,67 |
0,10 |
1,26 |
|
973 |
– 25,92 |
1,40 |
24,72 |
|
1073 |
– 50,16 |
2,44 |
277,97 |
|
1173 |
– 7440 |
3,31 |
2074,91 |
|
1273 |
– 98,65 |
4,05 |
1271,97 |




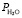 , Па
, Па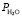 , Па
, Па