В настоящее время в области анализа и проектирования устройств аналоговой электроники (устройства отображения информации, системы автоматического управления, аналоговые фильтры) наблюдаются попытки перехода на уровень выпуска системных микросхем, однако отсутствие единого общепризнанного математического аппарата решения задач анализа и синтеза сдерживают развитие данного направления. Выход из создавшегося положения наметился в работе [2], где за естественнонаучную базу аналоговой микроэлектроники принята математическая теория систем дифференциальных уравнений (ДУ) в обобщенной форме. Переход к естественнонаучным представлениям позволяет сформировать новый элементный базис. Необходимым шагом перехода на новую элементную базу является замена модели радиоэлектронного устройства в виде принципиальной электрической схемы на равноценную модель в виде структурной схемы, которая должна состоять только из элементарных звеньев предлагаемой элементной базы [2, 9]. Важным шагом перехода на предлагаемую элементную базу является обоснование процедуры синтеза электронного устройства: выбор структуры дифференциального уравнения; расчет его коэффициентов и сборка синтезируемого устройства. Всё это, вместе взятое, определяет новый подход к анализу и синтезу электронных устройств на элементарных звеньях. На основе вновь введенной элементной базы возможно сформировать как МАБИС (матричные аналоговые большие интегральные схемы), так и ПАИС (программируемые аналоговые интегральные схемы). Такая возможность обусловлена малочисленностью элементов в базе и позволяет спроектировать уникальный чип для данной МАБИС, или единый перепрограммируемый элемент для ПАИС [2].
Однако те большие возможности, которые открываются введением предлагаемой элементной базы, требуют обширной предварительной работы, связанной с исследованием особенностей проектирования различных типов аналоговых устройств. В настоящей статье предлагается алгоритм синтеза таких широко применяющихся устройств, как фильтры. Для синтеза фильтров предлагается использовать аппарат матричных операторов, который хорошо зарекомендовал себя для решения задач управления для класса линейных стационарных и нестационарных систем [1, 3, 7], а в последнее время нашел развитие и на класс нелинейных систем [4, 5, 6, 10, 13]. Рассмотрим алгоритм решения задачи синтеза оптимального фильтра на конкретном примере. Предположим, что система задана следующей структурной схемой (рис. 1).
Рис. 1. Структурная схема системы
Динамика объекта описывается уравнением
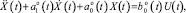(1)
где
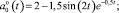
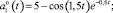
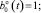
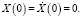
На вход системы поступает аддитивная смесь центрированных не коррелированных сигналов m(t) (полезный сигнал) и n(t) (помеха) с известными корреляционными функциями
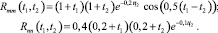(2)
Требуется синтезировать последовательное корректирующее устройство (фильтр), которое устранило бы влияние помехи на выходной процесс X(t) системы на промежутке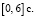 
Решение поставленной задачи представим в виде последовательности этапов.
Этап 1. Выберем в качестве ортонормированного базиса (ОНБ) ортонормированные на промежутке [0, 6] полиномы Лежандра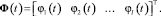 
Этап 2. Проведем статистический анализ системы без фильтра. Структурная схема системы в операторной форме представлена на рис. 2 (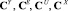
– спектральные характеристики входного сигнала, сигнала ошибки, управления и выходного сигнала соответственно; Аф, А0 – матричные операторы фильтра и объекта).
Рис. 2. Структурная схема системы в операторном виде
Задав размер базиса l = 12, одним из способов, изложенных в [11, 12], найдем матричный оператор объекта А0 в выбранном базисе. Далее определяем матричный оператор всей системы без регулятора: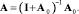 
Применяя двумерное преобразование Фурье, рассчитываем спектральные характеристики корреляционных функций полезного сигнала и помехи:
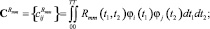
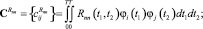
По следующим зависимостям определяем спектральные характеристики корреляционной функции выходного сигнала, обусловленные действием: полезного сигнала и помехи –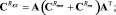 
полезного сигнала – 
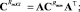помехи – 
.
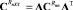При синтезе фильтра спектральную характеристику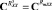 
(обусловленную действием только полезного сигнала) будем использовать в качестве желаемой (эталонной). По формуле
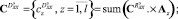
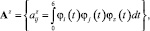
рассчитаем спектральную характеристику желаемой дисперсии выходного процесса.
Найдем автокорреляционные функции, дисперсии и среднеквадратическое отклонение (СКО) выходного сигнала, обусловленные действием:
– полезного сигнала и помехи
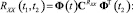
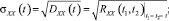
– полезного сигнала
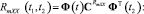
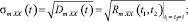
– помехи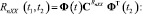 
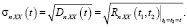
Графики СКО выходного сигнала, обусловленные совместным действием полезного сигнала и помехи, а также действием отдельно помехи и полезного сигнала, представлены на рис. 3.
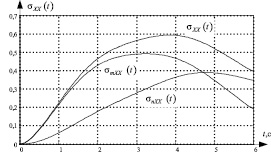
Рис. 3. Графики СКО выходного сигнала системы без фильтра
Этап 3. Расчет оптимального матричного оператора фильтра. Вычислим матричный оператор фильтра относительно двух критериев: критерия близости корреляционных функций и критерия близости дисперсий. Матричный оператор системы с фильтром имеет вид
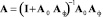. (3)
Оптимальные матричные операторы найдем из следующих зависимостей:
- критерий близости корреляционных функций:
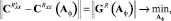(4)
где
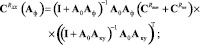
- критерий близости дисперсий:
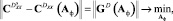(5)
где
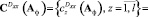
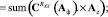
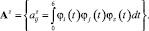
Выбрав евклидову норму матриц (4), (5), получим следующие целевые функции, подлежащие минимизации относительно элементов матрицы Аф:
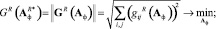
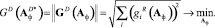
Положив в качестве начального приближения Аф = I, (I – единичная матрица) методом Гаусса – Ньютона вычисляем оптимальные матричные операторы фильтра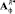 
, 
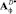, при этом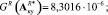 
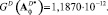
Этап 4. Построение математической модели оптимального фильтра в форме дифференциального уравнения по известным матричным операторам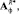 
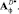Имеется несколько подходов к решению этой задачи, один их них основан на использовании понятия порождающих функций [11]. В случае если порядок ДУ невысокий, можно предложить следующий способ. Зададим следующую структуру ДУ, описывающее динамику фильтра:
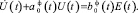(6)
Определим коэффициенты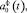 
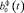в виде разложения по ОНБ так, чтобы матричный оператор уравнения (6) Аф как можно точнее совпадал с 
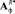в одном случае и с 
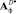в другом. Матричные операторы правой 
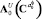и левой 
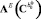частей уравнения (6) можно представить следующим образом (см. переход о ДУ к соответствующему интегральному уравнению в [11]):
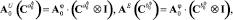
где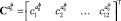 
– спектральная характеристика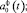 
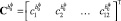– спектральная характеристика 
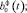элементы матрицы 
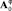согласно вычисляются следующим образом:
,
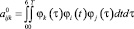а ее структура имеет размер (12*122):
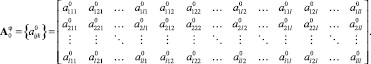
Тогда матричный оператор фильтра определяется следующим образом:
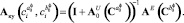(7)
Оптимальные параметры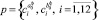 
найдем исходя из следующих зависимостей:
– критерий близости корреляционных функций:
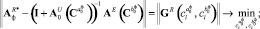(8)
– критерий близости дисперсий:
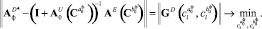(9)
Задавшись евклидовой нормой для матриц (8), (9), получим следующие целевые функции, подлежащие минимизации:
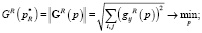
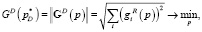
где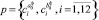 
– совокупность искомых параметров.
В результате минимизации целевых функций методом Гаусса – Ньютона были найдены: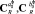 
– спектральные характеристики соответствующих коэффициентов фильтра, найденные по критерию (8); 
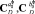– спектральные характеристики, найденные по критерию (9).
Целевые функции при оптимальных параметрах принимают следующие значения:
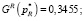
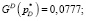
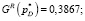
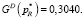
Этап 5. Анализ системы с найденными фильтрами. Матричные операторы всей системы:
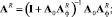
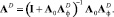
Спектральные характеристики выходного сигнала, обусловленные воздействием полезного сигнала и помехи:
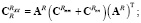
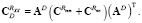
Автокорреляционные функции, дисперсии и СКО выходного сигнала, обусловленные действием полезного сигнала и помехи:
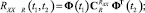
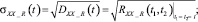
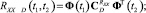
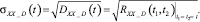
На рис. 4 представлены графики СКО выходного сигнала с фильтром, построенным на основе равенства корреляционных функций выходного и эталонного процессов (фильтр 1) и на основе равенства дисперсий выходного и эталонного процессов (фильтр 2). В случае получения результата с недостаточной точностью, необходимо на этапе 4 задать более сложную структуру фильтра.
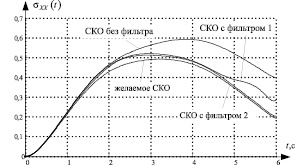
Рис. 4. Графики СКО выходного сигнала системы
Предложенный подход к построению фильтров, основанный на методе матричных операторов, позволяет найти ДУ оптимальных фильтров, как для класса стационарных, так и нестационарных случайных процессов, причем нет ограничений и на стационарность объекта. Все это позволяет широко использовать элементный базис аналоговой микроэлектроники для сборки синтезируемого устройства.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Калужской области (гранты № 14-48-03013, № 16-41-400701).