Пространственные объекты отличаются своей сложностью и разнородностью. Также неоднороден и характер расположения данных объектов. При этом пространственные объекты в той или иной степени взаимосвязаны между собой. Например, дорога «упирается» в здание или дорога огибает здание. От того, насколько точно и полно хранится информация в геоинформационной системе (ГИС) о взаимоотношении объектов, зависит качество решения многих задач. В настоящее время многие ГИС решают данную проблему неэффективно, т.к. отношения между объектами в них не описаны или малоинформативны. Для более полного решения задач необходимо использовать новые подходы и методы описания взаимодействия объектов.
Цель работы
В данной работе анализируются способы описания топологических отношений между пространственными объектами на основе принципов интеллектуализации геоинформационных систем.
Результаты исследования и их обсуждение
Основой описания взаиморасположения картографических объектов являются топологические отношения. Топология делает возможным проведение расширенного пространственного анализа и играет фундаментальную роль в обеспечении качества данных ГИС. Если топологические отношения между объектами ГИС отличаются от отношений между реальными объектами, это существенно снижает качество карты.
Топологические отношения используются в картографии, на транспорте, при описании инженерных сетей. Например, наличие топологических отношений позволяет оперативно найти отключающие или изолирующие устройства (краны, задвижки) при аварии на трубопроводе.

а) б)
Рис. 1. а) Трубопровод соединен с основной магистралью (наличие топологических отношений); б) Трубопровод не соединен с основной магистралью (отсутствие топологических отношений)
Два наиболее общих типа топологических запросов в геоинформационных системах:
- Найти все объекты, находящиеся в топологическом отношении R с данным объектом;
- В каком топологическом отношении находятся объекты А и В?
Существуют различные подходы к описанию данных отношений. Наиболее общим является теоретико-множественный подход [3], в котором топология базируется на таких понятиях, как непрерывность, граница, замкнутость и множество внутренних точек, которые могут быть определены посредством соотношения окрестностей точек пространственных объектов. Бинарные топологические отношения между двумя объектами А и В на плоскости R2 основаны на пересечении границы (∂A), внутренней (A0) и внешней (A–) области объекта А с границей (∂B), внутренней (B0) и внешней (B–) областью объекта В. Матрица девяти пересечений шести частей объектов определяет топологические отношения и может быть кратко представлена следующим образом:
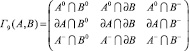 .
.
Рассматривая значения «пусто» (0) и «непусто» (1), можно выделить 29 = 512 бинарных топологических отношений. Для двухмерной области, вложенной в R2, можно представить восемь отношений, обеспечивающих полное, взаимно исключающее покрытие. Этими отношениями являются непересекающийся, соприкасаться, перекрывать, равный, содержит, внутри, покрывает и покрыт. Указанная модель топологических отношений полностью описывает пространственные отношения между объектами на уровне констатации факта отношения, но не содержит средств описания характера отношения. Например, если два региона касаются в двух точках, в модели будет зафиксирован только факт касания.
Во многих известных ГИС анализируется взаимное влияние посредством координатной составляющей [1]. Однако многие тематические карты одной и той же территории могут иметь различные масштабы, также в зависимости от типа и времени съемки может возникнуть несоответствие между пространственными объектами.
Также для описания топологических отношений пространственных объектов широко применяют графовые модели [8, 10]. В этих моделях могут быть использованы разные виды отношений. При этом следует отличать пространственный граф, который содержит пространственную топологию от описательного графа, который содержит дополнительное описание. То есть цифровая карта, имеющая топологическую структуру, представляет собой пространственный граф, т.е. набор точек на местности (узлов), соединенных ломаными линиями – дугами. А дугам описательного графа может быть поставлено в соответствие некоторое число – одна из характеристик объекта, например качество дорожного покрытия.
Следует тщательно планировать пространственные отношения объектов в ГИС. Некоторые правила топологии управляют отношениями объектов в пределах одного класса объектов, другие – управляют отношениями между объектами в двух различных пространственных классах.
В ГИС наиболее распространены три типа топологий [7]:
- Точечная;
- Сетевая;
- Полигональная.
Точечная топология строится из точечных объектов (рис. 2). На рис. 2 точечная топология образована адресами пунктов потребителей.
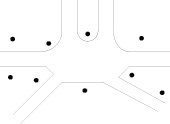
Рис. 2. Точечная топология пунктов потребителей
Точечная топология описывается классом объектов 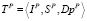 , свойствами которого являются IP – имя топологии; SP – тип; DpP – число точек.
, свойствами которого являются IP – имя топологии; SP – тип; DpP – число точек.
Сетевая топология строится из линейных объектов и может включать точечные объекты. Наиболее распространенная область применения сетевой топологии – анализ транспортных сетей. Сетевые топологии позволяют решать некоторые оптимизационные задачи из теории графов: определение степени связности, кратчайшего расстояния и др.
Сетевая топология устанавливает, чтобы внутри одного класса пространственных объектов не было совпадающих линий, линии не пересекались, не имели висячих узлов и т.д.
На рис. 3 для примера изображен участок городской транспортной сети.
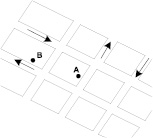
Рис. 3. Сетевая топология автодорог
При решении задач управления материальными потоками поиска кратчайшего пути описание транспортной сети сетевой топологией дает возможность задать смежность участков дорог (с учетом разрешающих поворот дорожных знаков) и определить направление (на рис. 4 показано стрелками) движения. Если участок описан как сетевая топология, с помощью соответствующего метода класса может быть найден и построен на карте кратчайший путь между указанной парой точек сети А и В (рис. 4).
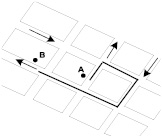
Рис. 4. Кратчайший путь между точками А и В на сети
Сетевая топология описывается классом объектов 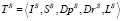 , свойствами которых являются: IS – имя топологии; SS – тип; DpS – число точек; DrS – число ребер, соединяющих пары точек; LS – длина ребер.
, свойствами которых являются: IS – имя топологии; SS – тип; DpS – число точек; DrS – число ребер, соединяющих пары точек; LS – длина ребер.
Полигональная топология строится из двумерных объектов. Данный вид топологии используется при моделировании земельных участков, административно-территориальных единиц, различных тематических зон (например, зон функционирования супермаркетов и торговых центров). Пример полигональной топологии приведен на рис. 5.
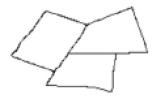
Рис. 5. Полигональная топология «соседства» земельных участков
Полигональная топология описывается классом объектов
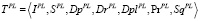 ,
,
свойствами которого являются: IPL – имя топологии; SPL – тип; DpPL – число точек; DrPL – число ребер, соединяющих пары точек; DplPL – число полигонов; PrPL – периметр; SqPL – площадь.
Полигональная топология требует, чтобы полигоны в пространственном классе не перекрывали друг друга, не имели разрывов и т.д. Например, можно убедиться, что все полигоны участков образуют замкнутые контуры, что они не перекрываются и что между участками нет промежутков.
Можно также использовать топологию для проверки пространственных отношений между объектными классами. Например, можно удостовериться, что линии границ землеотводов в созданной модели данных имеют общую совпадающую геометрию с границами земельных участков.
Однако в связи с интеллектуализацией ГИС понятие топологии приобретает новый смысл. Интеллектуальные ГИС должны обеспечивать комплексный анализ и интерпретацию разнородных данных, поддержку принятия решений и моделирование рассуждений о пространственной ситуации с учетом различных НЕ-факторов [4, 6]. Под интеллектуальной ГИС (ИГИС) будем понимать сложный программный продукт, включающий как непосредственно саму ГИС, так и различные элементы искусственного интеллекта для решения задач, содержащих неполноту, неоднозначность, неточность информации [2, 5]. Основной частью интеллектуальной ГИС является база знаний, которая представляет собой хранилище экземпляров абстракций реальных объектов и связей между ними.
Следующим важным компонентом ИГИС является экспертная система, включающая в себя машину логического вывода и набор логических правил. Обычно она представляет собой ориентированную на правила систему, предназначенную для обработки знаний, хранящихся в базе знаний. Правила-продукции являются частью экспертной системы и имеют следующий вид:
IF Условие THEN Действие.
Здесь Условие – четкое или нечеткое высказывание, Действие – четкая или нечеткая команда на поиск или изменение.
Для получения выводов, продукции могут образовывать сложные цепочки. Описания правил так же могут храниться в базе знаний, как часть описания предметной области. Экспертная система служит для решения двух задач в ИГИС. Первая из них традиционна для экспертных систем и заключается в выдаче рекомендаций в сложных для принятия решения ситуациях. Вторая задача – управление сложными режимами моделирования.
Интеграция геоинформационной системы и экспертной системы расширяет круг решаемых ими задач и открывает путь для более гибкого и комплексного анализа отношений между пространственными объектами, основанного на правилах и логических выводах.
Процесс анализа топологических отношений в некоторых областях пространства базируется на оценке различных характеристик объектов [9], например:
- форма пространственных объектов одинакова, однако размер разный;
- объекты совпадают по форме и размеру, однако расстояние между ними различно и т.д.
Поэтому в ГИС при описании топологических отношений необходимо учитывать следующие их составляющие:
- функциональные (определяют влияние одних объектов на другие);
- количественные (далеко, близко);
- пространственные (за, под, над…);
- атрибутивные (иметь свойство, иметь значение);
- логические (И, ИЛИ, НЕ);
- концептуальные (задают правила образования топологии).
Таким образом, под топологическим отношением пространственных объектов в ГИС понимаем отношение xRy, в котором R = <F, Pr, At, Kv, L, Con>, где F = {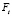 },
}, 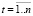 – множество функциональных составляющих; Pr = {
– множество функциональных составляющих; Pr = {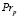 },
}, 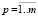 – множество пространственных взаимоотношений; At = {
– множество пространственных взаимоотношений; At = {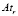 },
}, 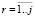 – множество атрибутивных значений; Kv = {
– множество атрибутивных значений; Kv = {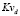 },
}, 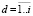 – множество количественных отношений; L = {
– множество количественных отношений; L = {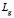 },
}, 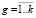 – множество логических правил; Con = {
– множество логических правил; Con = {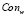 },
}, 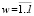 – множество концептуальных правил.
– множество концептуальных правил.
Данный подход описания топологических отношений позволяет оценивать также степень близости и связанности пространственных объектов. Анализ топологических отношений происходит на основе правил экспертной системы.
Например, пространственный объект Obj1 находится справа (Pr1) от Obj2 на расстоянии Kv1 и Obj3 располагается под (Pr3) Obj2 на расстоянии Kv2. Таким образом, правило топологии имеет вид
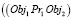 и
и 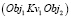 и
и 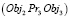 и
и 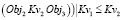 =>
=>
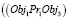 и
и 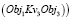 ;
;
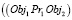 и
и 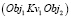 и
и 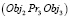 и
и 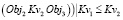 =>
=>
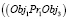 и
и 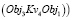 .
.
Другой пример: пространственный объект Obj1 размещается над (Pr4) объектом Obj2 на расстоянии Kv3 и Obj3, располагается под (Pr3) Obj2 на расстоянии Kv4. То правило топологии будет иметь вид
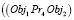 и
и 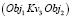 и
и 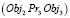 и
и 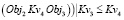 =>
=>
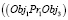 и
и 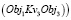 ;
;
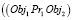 и
и 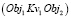 и
и 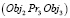 и
и 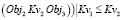 =>
=>
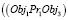 и
и 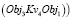 .
.
Выводы
Таким образом, топологические отношения являются основой работы любой ГИС. Их использование позволяет качественно структурировать пространственно-распределенные данные. При помощи топологии пространственным данным присваивается поведение реальных ГИС-объектов. Использование различных составляющих при описании топологических отношений позволяет на качественно новом уровне моделировать поведение пространственных объектов. Правила-продукции вывода топологий являются структурной составляющей интеллектуальной оболочки ГИС.



