Существует ряд подходов и разработано множество моделей, моделирующих движение дискретных многомассовых систем в вибрирующем контейнере [2].
Существенным недостатком разработанных моделей является то, что процедура моделирования даже двух секунд процесса выполняется от двух часов и более. Поэтому снижение времени моделирования – это очень актуальная задача. Снижение времени предполагается выполнить за счет распараллеливания вычислений, что в свою очередь требует построения специальной модели и алгоритма системы. Автором предлагается следующий подход к моделированию многомассовых систем, при котором параллельно, при помощи видеокарт NVIDIA, с использованием архитектуры вычислений CUDA отслеживаются параметры движения отдельных частиц, их упругое взаимодействие друг с другом и со стенками контейнера и выполняется визуализация процесса.
Теоретический анализ
В 2000 г. профессором С.Н. Шевцовым и А.А. Петряевым была разработана программа моделирования динамики быстрых движений гранулированных сред GranMos [3, 5].
Система GranMoS предназначена для моделирования динамики гранулированных сред при воздействии на них внешнего механического возбуждения со стороны границ. Сконструировав систему, т.е. задав размеры и физико-механические свойства сферических гранул, форму ограничивающего контейнера и закон его движения, законы взаимодействия гранул друг с другом и с границами, системе предоставляют возможность развиваться в соответствии с законами динамики.
Процесс моделирования в этой программе может занимать от нескольких минут до десятков часов. Завершив моделирование, можно увидеть движение системы частиц в реальном времени, поле скоростей и плотности частиц. Система используется для проектирования технологических машин, работающих с гранулированными средами: вибростанков, транспортеров, сепараторов, сит.
Материалы и методы исследования
В настоящей статье предлагается осуществить сокращение машинного времени моделирования за счет разработки эффективного вычислительного метода, использующего распараллеливание на базе многоядерных графических процессоров. Для этого были решены следующие задачи:
а) определены затраты времени на вычислительные процедуры на каждом этапе вычисления;
б) определены резервы сокращения времени;
в) оптимизированы алгоритм вычисления с распараллеливанием;
г) разработан эффективный вычислительный метод программы моделирования с распараллеливанием.
В связи с тем, что эффект сокращения времени моделирования наблюдается при большом количестве частиц, в настоящей работе для определения затрат времени используется контейнер и деталь круглой формы. Это позволяет исключить влияние формы контейнера и детали на ускорение вычислений (рис. 1).
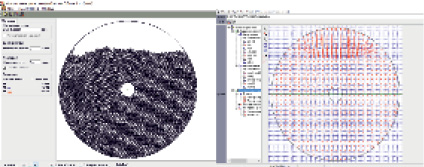
Рис. 1. Фрагмент интерфейса программы исследования процесса виброударного упрочнения детали и контейнера круглой формы
Для определения затрат времени выбирались контейнеры, форма которых представляет собой сплайн 1-й степени, с количеством сегментов в диапазоне от 200 до 800 и числом частиц инструментальной среды в диапазоне от 500 до 10000.
В результате исследования времени выполнения одного шага интегрирования системы выяснилось, что наиболее длительные (от 80 до 90 %) затраты времени «расходуются» на функцию расчета скоростей и ускорений для состояния ансамбля частиц. Остальные процедуры, включающие в себя процедуру обновления границы контейнера, а также функции предиктора, корректора в совокупности занимают не более 20 % процедуры шага интегрирования.
Одним из важных моментов исследования является то, что время моделирования одного шага интегрирования прямопропорционально количеству частиц инструментальной среды (рис. 2). На каждом шаге интегрирования движения ансамбля частиц для каждой частицы выполняются вычисления, не зависящие от результатов вычислений для остальных частиц ансамбля. В этом случае необходимо применить распараллеливание вычислений, которое даст значительное сокращение общего времени выполнения моделирования. Это подтверждается еще тем, что структура программы состоит из этапов, напрямую зависящих от количества частиц ИС и количества сплайнов.
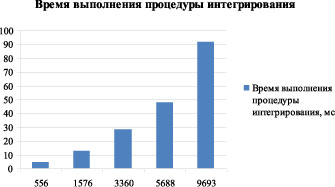
Рис. 2. Время выполнения процедуры интегрирования в зависимости от количества частиц ИС
Результаты исследования и их обсуждение
Рассматривается алгоритм интегрирования двумерной многомассовой системы, состоящей из n частиц и m сегментов сплайновых кривых, методом Адамса 4 порядка с предикт-коррекцией без распараллеливания (рис. 3). Вся процедура выполняется с использованием центрального процессора (ЦП) и ОЗУ хоста.
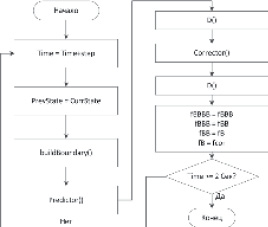
Рис. 3. Алгоритм процедуры интегрирования без распараллеливания
Шаг 1. В начале каждой итерации процедура интегрирования принимает значение времени time = time + step, где step – шаг по времени. Его характерное значение равно 10-6 с. Таким образом, для моделирования 1 секунды динамики многомассовой системы необходимо выполнить порядка миллиона итераций!
Шаг 2. Осуществляется копирование состояния предыдущего состояния ансамбля инструментальной среды в текущее состояние prevstate = currstate.
Шаг 3. Получение состояния сплайновой границы в момент времени time, при помощи вызова функции buildboundary. Здесь последовательно для каждого сегмента границы контейнера рассчитывается его положение в текущий момент time на основе его кинематической функции движения. Сложность шага O(m).
Шаг 4. Последовательное вычисление предиктора для каждой частицы инструментальной среды. Сложность шага O(n).
Шаг 5. Последовательное вычисление ускорений и скоростей для «предсказанного» состояния ансамбля частиц: fpr = D(time, currstate). Сложность шага линейно зависит от n и m.
Шаг 6. Последовательное вычисление корректора для каждой частицы инструментальной среды. Сложность шага O(n).
Шаг 7. Последовательное вычисление ускорений и скоростей для «скорректированного» состояния ансамбля частиц: fcor = D(time, currstate). Сложность шага аналогична шагу 6.
Шаг 8. Переопределение временных слоев.
Шаг 9. Переход к шагу 1, либо завершение работы при достижении заданного модельного времени.
Анализ алгоритма показывает, что, во-первых, самыми длительными по времени являются шаги 5 и 7, так как именно здесь происходит расчет сил, действующих на все элементы системы и между ними, и, во-вторых, вычисления на шагах 3, 4 и 6 можно легко распараллелить. Так как количество элементов системы лежит в диапазоне от нескольких сотен до нескольких десятков тысяч, то необходимо при распараллеливании вычислений применить аппаратные средства, которые могут генерировать примерно такое же количество потоков. В качестве таких средств в настоящей работе используются видеокарты с поддержкой технологии NVidia CUDA.
Процедура интегрирования двумерной многомассовой системы с распараллеливанием выполняется на основной системе (называемой термином хост), к которой подключен GPU – сопроцессор для массивно-параллельных вычислений, который по отношению к хосту называют устройством. CUDA-программа задействует CPU, где выполняется последовательная часть кода и подготовительные стадии для GPU вычислений, а параллельные участки кода переносятся на GPU, где будут выполняться большим множеством нитей [1, 4]. Исходный код программы прямого моделирования реализован в среде Delphi. Для того чтобы применить распараллеливание при помощи NVIDIA CUDA, необходимо текст кода с распараллеливанием операций реализовать в среде C++. Cвязано это с тем, что на текущий момент времени компилятор CUDA поддерживает только языки С, С++ и Fortran для ускорения приложений с помощью графических процессоров NVIDIA с массивно параллельной архитектурой. Все функции, написанные на С++, реализуются в форме динамической библиотеки, которая подключается к исходной программе моделирования на языке Pascal.
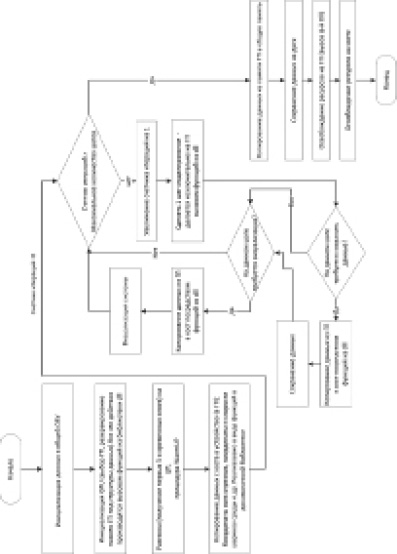
Рис. 4. Алгоритм процедуры интегрирования с распараллеливанием
Алгоритм моделирования с распараллеливанием (рис. 4) отличается тем, что процедура инициализации, которая производится вызовом функций из динамической библиотеки, выполняется как в общей ОЗУ хоста, так и устройства. Затем после выполнения процедуры разгонки «warmup», выполняющейся на CPU, осуществляется копирование всех данных, необходимых для моделирования системы (координат всех сплайнов, координаты и скорости частиц инструментальной среды и т.д.) с хоста на устройство и последующие 100 итераций интегрирования выполняются на устройстве посредством вызова функций из динамической библиотеки. Каждая из вызываемых функций реализована в виде вызова ядер CUDA, код в которых выполняется параллельно, т.е. внутри ядра одновременно происходят вычисления для каждой из частиц инструментальной среды и каждого сегмента детали. Таким образом, распараллелены вычисления на наиболее длительных шагах 3–7 (рис. 3).
При необходимости визуализации или сохранения данных или достижения счетчиком итераций максимального количества шагов, происходит копирование данных из памяти устройства в ОЗУ хоста, а затем освобождение ресурсов на хосте и устройстве.
Рассмотрим модель, содержащую 1576 гранул и 432 сплайна. Траектория движения контейнера по оси Ox и Oy задаются, как гармоническая осцилляция. Частицы инструментальной среды представляют собой стальные шарики. Время моделирования процесса виброударного упрочнения составило 685 с в реализации вычислений с распараллеливанием в сравнении с 7200 с без распараллеливания, что соответствует уменьшению времени моделирования в 10 раз.



