В настоящее время отсутствует объективная методика оценки численного соотношения между компонентами заполнителя, внесенного в рабочий зазор электромагнитных порошковых муфт (ЭПМ). В этой связи исследования физико-механических процессов, происходящих в магнитоожиженном слое ферропорошка под действием электромагнитного поля при относительном смещении поверхностей ЭПМ при различных коэффициентах заполнения рабочего зазора ферромагнитной составляющей являются актуальными. Актуальность исследования критерия для объективной оценки ферромагнитной составляющей заполнителя рабочего зазора ЭПМ также не вызывает сомнений при рассмотрении ряда эмпирических формул, характеризующих величину силы взаимодействия между ведущей и ведомой частями ЭПМ при различных значениях индукции Bδ в их рабочих зазорах [2, 3]. Представленные в статье результаты исследований имеют практическую значимость и могут быть использованы при проектировании надежно работающих ЭМП в аппаратурно-технологических системах АПК.
Целью исследования является разработка методики объективной оценки количества ферромагнитной составляющей в рабочем зазоре электромагнитных порошковых муфт (ЭПМ).
Материалы и методы исследований
Объективный критерий оценки количества ферромагнитной составляющей в рабочем зазоре ЭПМ. Использованы экспериментально-статистические методы исследований.
Результаты исследования и их обсуждение
Основным фактором, определяющим вращающий момент, передаваемый ЭПМ, является удельное усилие сдвига (τ или f), величина которого зависит от магнитной индукции Bδ в рабочем зазоре, величины рабочего зазора δ, сорта заполнителя, его состава и ряда конструктивных факторов [1, 4, 5, 6]. Ферромагнитный порошок пропорционально магнитному полю увеличивает свою вязкость благодаря образованию связок, ориентированных вдоль магнитных силовых линий, и осуществляет, таким образом, сцепление полумуфт и передачу момента (рис. 1). Сухие порошковые муфты (смесь ферромагнитного порошка с тальком, графитом и т.п.) имеют диаметр зерен в пределах 0,5–10 мкм. Передача момента осуществляется за счет сил трения, развиваемых в слое скольжения (или в зоне разрушения) структурных построений между ферротелами. Такая трактовка процессов в рабочем зазоре ЭПМ согласуется с полученными экспериментальными данными, выполненными на макетах, моделирующих рабочий объем исследуемых аппаратов. Угол разрыва связок θ0 является в действительности углом деформации структурных построений из ферротел заполнителя. Экспериментально установлено, что угол θ0 достигает величины 16–20 ° при индукции в рабочем зазоре B = 0,3 – 0,4 Тл.
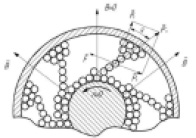
Рис. 1. Организация связок из ферропорошка заполнителя в зазоре ЭПМ: В – индукция магнитного поля; n – частота вращения вала, F – силы взаимодействия между частицами ферропорошка заполнителя; τ – тангенциальное усилие сдвига; ν – угол деформации связок из ферропорошка заполнителя
В настоящее время для определения составляющей удельного усилия сдвига (тангенциальная составляющая τ или f) [7, 8] используют следующие выражения:
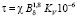; (1)
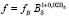, (2)
где KV – отношение объема материала магнитного порошка ко всему объему рабочего зазора; fB – постоянный коэффициент, зависящий от концентрации смеси, величины рабочего зазора и свойств ферромагнитной составляющей.
Естественно, что при различном заполнении (концентрации) рабочего зазора ферромагнитным заполнителем величины τ и f , определенные по выражениям (1) и (2), при прочих равных условиях будут различными. Поэтому весьма важно однозначно характеризовать степень заполнения рабочего зазора заполнителем и, в частности, его ферромагнитной составляющей.
До сих пор еще нет единого объективного подхода к определению степени заполнения объема рабочего зазора тем или иным заполнителем. Этим, очевидно, можно объяснить то, что в исследованиях используют формулу Лихтенеккера, характеризующую зависимость начальной магнитной проницаемости магнитодиэлектрика от концентрации соответствующего карбонильного порошка
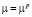, (3)
где µ – проницаемость магнитодиэлектрика;
p – объемная концентрация ферромагнитной основы.
Применительно к определению средней магнитной проницаемости заполнителя объемная концентрация ферромагнитной основы представлена в следующем виде:
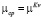, (4)
где µ – значение магнитной проницаемости вещества ферромагнитных частиц;
KV – коэффициент объемного заполнения магнитной средой.
По сравнению с экспериментом формула (4) дает ошибку при KV = 0,5 больше 15–70 %. При этом под насыпным весом заполнителя подразумевают вес его единичного объема, не меняющегося при его свободной утряске, т.е. утряске под действием собственного веса. Такой подход к определению связи между весом и объемом, заполняемым частицами заполнителя, является необъективным и вносит ошибку субъективного характера в определение величины коэффициента KV.
При этом коэффициент заполнения KV рабочего зазора определяют по выражению
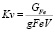, (5)
где GFe – вес ферромагнитных частиц в смеси;
gFe – удельный вес материала частиц ферромагнитной составляющей;
V – объем заполнителя.
Эта рекомендация для определения KV также носит субъективный характер. В зависимости от интенсивности встряхивания заполнитель может занимать различный объем. В основном это определяется формой частиц заполнителя (его компонентов) и способами его уплотнения в данном объеме. При этом не учитывается величина объема рабочего зазора, в который вносится заполнитель (с учетом изоляции его от внутренних полостей ЭПМ).
Следует, по-видимому, пользоваться двумя различными по содержанию понятиями «коэффициент заполнения рабочего зазора».
Коэффициент заполнения объема рабочего зазора ферромагнитной составляющей заполнителя – это понятие, которое можно применить к заполнителю на любой основе. Именно ферромагнитная составляющая в основном характеризует свойства заполнителя рабочего зазора. Коэффициент заполнения объема рабочего зазора ферромагнитной составляющей заполнителя KVFe предлагается определить по следующей формуле:
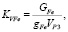(6)
где GFe – вес ферромагнитной составляющей заполнителя, внесенного в рабочий зазор;
gFe – удельный вес ферромагнитной составляющей заполнителя;
VРЗ – объем, отделенный от внутренних полостей ЭПМ.
Формулу (5) целесообразно применять только при рабочем зазоре, изолированном от внутренних полостей ЭПМ, так как лишь в этом случае можно говорить о стабильном значении коэффициента KVFe.
Определенный по формуле (6) коэффициент заполнения KVFe будет однозначно характеризовать магнитные свойства рабочего зазора, в частности его магнитное сопротивление в статических условиях. Эта формула удобна для определения коэффициента KVFe на жидкой основе. В этом случае подразумевается, что почти весь объем рабочего зазора заполнен ферромагнитной составляющей в смеси с каким-либо маслом и с учетом температурного коэффициента объемного расширения последнего при повышении его температуры в процессе работы со скольжением [9, 10].
Для характеристики магнитного состояния заполнителя в рабочем зазоре при использовании твердой основы необходимо также располагать значением коэффициента заполнения. В этом случае должна быть учтена форма частиц ферромагнитной составляющей и твердой основы заполнителя. Появляется (и косвенно учитывается с помощью специально вводимых коэффициентов) третья компонента заполнителя рабочего зазора – воздух в промежутках между частицами заполнителя.
Коэффициент заполнения рабочего зазора на твердой основе определяется по формуле
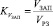, (7)
где VЗАП – объем заполнителя на твердой основе.
Объем порошкового заполнителя складывается из объемов по крайней мере двух порошкообразных компонентов:
VЗАП = (VK1 + VK2) K3, (8)
здесь VK1 – объем первой компоненты (ферромагнитной составляющей);
VK2 – объем второй компоненты (твердая основа);
K3 – коэффициент, учитывающий различие в форме частиц компонентов заполнителя.
Коэффициент K3 характеризует плотность заполнения заполнителем единичного объема.
Объем, занимаемый частицами первой компоненты, определяется по формуле
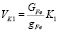, (9)
где K1 – коэффициент, учитывающий влияние формы частиц ферромагнитного порошка на величину занимаемого им объема.
Численное значение коэффициента K1 определяется по известным формулам для частиц сферической и неправильной формы.
Объем, занимаемый частицами второй компоненты, определяется по выражению
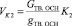, (10)
где GТВ.ОСН. – вес твердой основы;
gТВ.ОСН. – удельный вес материала твердой основы;
K2 – коэффициент, учитывающий влияние формы частиц на величину занимаемого ими объема.
Объем, занимаемый заполнителем, составленным из двух компонентов, определяется выражением
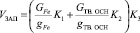. (11)
На основании изложенного можно утверждать, что коэффициент заполнения рабочего зазора заполнителем на твердой основе целесообразно вычислять по формуле
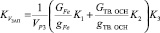. (12)
Формулой (12) имеет смысл пользоваться лишь при рабочем зазоре, изолированном от внутренних полостей ЭПМ. Анализ проведенных экспериментальных исследований показал, что величина, определенная по формуле (12), не зависит от субъективных действий экспериментатора. В этом случае таблицы, составленные для значений f (или τ) и µ для ряда заполнителей при коэффициентах, определенных по формуле (12), будут содержать (при прочих разных условиях) их единственные значения.
Установлено, что магнитное сопротивление рабочего зазора при многократном его заполнении заполнителем без учета значения коэффициента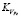 
будет различным. Проведены исследования магнитных характеристик заполнителей на твердой основе (тальк, слюда) с различными ферромагнитными компонентами. Заполнитель составлялся в каждом случае из двух компонентов. Зависимость тангенциальной составляющей сил взаимодействия между частицами ферропорошка от индукции в рабочем зазоре исследовалась на модели рабочего зазора ЭПМ для статических испытаний (рис. 2).
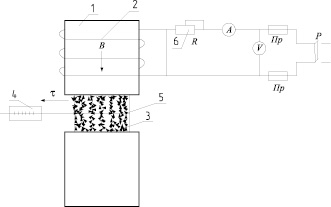
Рис. 2. Схема экспериментальной установки «Электромагнит ФЛ-1» для статических испытаний физико-механических процессов в рабочем зазоре ЭПМ: 1 – сердечник с подвижными полюсами электромагнита; 2 – обмотка управления; 3 – емкость с исследуемым заполнителем; 4 – стальная лента с динамометром; 5 – связки из ферропорошка; 6 – регулировочный реостат; А и V – соответственно амперметр и вольтметр в цепи обмотки управления
Расстояние между рабочими поверхностями соответствовало ширине рабочего зазора ЭПМ. В рабочий зазор VРЗ вносилось соответственно 35; 52; 70 г ферромагнитной составляющей, тщательно размешанной с порошкообразной слюдой, обеспечивающей достаточно полное заполнение рабочего зазора. Это соответствовало значениям коэффициентов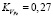 
; 
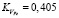и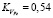 
. Скорость протяжки стальной ленты на макете, моделирующем рабочий зазор ЭПМ, и линейная скорость диска на уровне рабочего зазора с заполнителем относительно заторможенной части устанавливались одного порядка.
Определение величин B и H в рабочем зазоре производилось баллистическим методом. В результате исследований при оптимальном значении коэффициента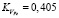 
[7] получена эмпирическая формула для исследуемой зависимости B = φ1(H). Для аналитического выражения кривой намагничивания заполнителя использована гиперболическая зависимость
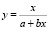
или
; 
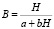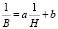. (13)
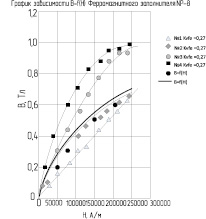
Спрямление зависимостей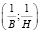 
, представленных на рис. 3, подтверждает, что данные опытной зависимости B = φ1(H) могут быть уложены в предлагаемое аналитическое выражение. Зависимость B = φ1(H) опишем аналитически для значений индукции (B = 0,1 – 0,6 Тл), т.е. для рабочего диапазона изменения индукции в рабочем зазоре ЭПМ. Величины постоянных коэффициентов a и b, входящих в формулу (12), определены методом наименьшей ошибки. Можно записать, что
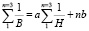
здесь n = 3.
В результате произведенных вычислений получаем, что а = 0,305; b = 0,4*10-4. Эмпирическая формула, описывающая зависимость B = φ1(H) заполнителя с порошком № Р-8 при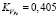 
, будет иметь следующий вид:
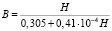. (14)
Значения индукции B, вычисленные по формуле (13), дают хорошее совпадение с соответствующими точками на опытной кривой B = φ1(H), представленной на рис. 3.
|
|
|
|
Рис. 3. График зависимости В-Н ферромагнитного заполнителя |
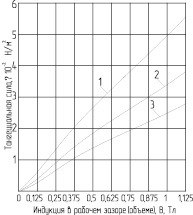
Рис. 4. Зависимость тангенциальной составляющей сил взаимодействия между феррочастицами заполнителя от индукции в рабочем зазоре В при высоте рабочего зазора (объема) М: 1 – δ = 0,25 мм; 2 – δ = 0,5 мм; 3 – δ = 1,5 мм |
Учитывая неоднородность и дискретность фрикционных контактов, тангенциальная составляющая силы Pτ взаимодействия между феррочастицами заполнителя в слое разрыва связок (между плоскостями) равна сумме элементарных сил трения Δτ, возникающих на отдельных площадках касания. Зависимость Pτ от индукции в рабочем зазоре В исследовалась на модели рабочего зазора ЭПМ для статических испытаний. Результаты экспериментальных исследований представлены на рис. 4.
Заключение
На основании результатов исследований физико-механических процессов, происходящих в магнитоожиженном слое ферропорошка под действием постоянного по знаку и регулируемого по величине электромагнитного поля при относительном смещении поверхностей, ограничивающих рабочий зазор ЭПМ, составлена методика объективной оценки численного соотношения между компонентами заполнителя электромагнитных порошковых муфт (ЭПМ). Представлены экспериментальные зависимости тангенциальной составляющей сил взаимодействия между феррочастицами заполнителя от индукции в рабочем зазоре ЭМП. Представленные в статье результаты исследований имеют практическую значимость и могут быть использованы при проектировании надежно работающих ЭМП в аппаратурно-технологических системах АПК.