Линейные электродвигатели находят достаточно широкое применение в различных отраслях промышленности и на транспорте. Поэтому работы по исследованию, разработке и внедрению таких машин интенсивно ведутся как в России, так и в других странах.
По конструктивным и экономическим соображениям вторичный элемент линейного асинхронного двигателя с двухсторонним индуктором (ДЛАД) выполняется из сплошной немагнитной полосы. В транспортных системах с ДЛАД вторичный элемент часто бывает смещён в поперечном направлении относительно индуктора, что обусловлено односторонним креплением вторичного элемента к путевой структуре и рабочим смещением в процессе эксплуатации.
В ряде случаев оказывается целесообразным искусственно смещать вторичный элемент в поперечном направлении относительно индуктора для изменения тягового усилия и скорости движения. Возникающее при этом поперечное усилие может быть использовано как рабочее в некоторых устройствах специального назначения [1–4].
Ограниченность ширины индуктора и вторичного элемента ДЛАД приводит к неравномерному распределению электромагнитного поля в поперечном направлении. Неравномерность распределения поля ещё больше возрастает при поперечном смещении вторичного элемента относительно индуктора.
При ограниченной ширине индуктора и вторичного элемента возникают поперечные усилия F1 и F2, показанные на рис. 1. Эти усилия обусловлены взаимодействием продольных составляющих индуцированного во вторичном элементе тока с нормальной составляющей магнитной индукции в зазоре, возбуждаемой обмоткой индуктора. Результирующее поперечное усилие в этом случае оказывается равным нулю.
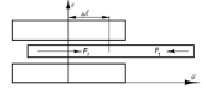
Рис. 1. Поперечное усилие при смещении вторичного элемента
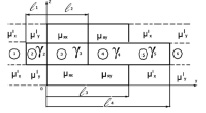
Рис. 2. Расчетная модель ДЛАД при поперечном смещении вторичного элемента
Поперечное смещение немагнитного вторичного элемента приводит к асимметрии индуцированных токов и магнитных полей по ширине вторичного элемента. Поэтому усилие F1 становится больше, чем усилие F2, и появляется неуравновешенное поперечное усилие Fп = F1 – F2, которое всегда будет направлено в сторону смещения вторичного элемента.
Для аналитического исследования характеристик ДЛАД при поперечном смещении вторичного элемента относительно индуктора была разработана расчетная модель, позволяющая учесть реальный характер электромагнитного поля в боковых зонах. Эта модель показана на рис. 2.
В основу расчетной модели положены следующие допущения:
1. Длина ДЛАД достаточно велика и продольный краевой эффект отсутствует.
2. Наличие пазов на поверхности индуктора учитывается соответствующим увеличением зазора.
3. Вторичный элемент полностью заполняет эквивалентный зазор δ′, имеет расчетные электропроводности γ2 – γ5 и движется с постоянной скоростью в направлении оси x. Ось Х перпендикулярна плоскости рисунка.
4. Магнитная проницаемость в зонах 1–6 по направлению оси Z равна µ0, а по направлению осей X и Y принята равной нулю [5]. При этом в зазоре будет только одна составляющая магнитной индукции, совпадающая по направлению с осью Z.
5. Магнитная проницаемость ярма индуктора по направлению оси Z равна бесконечности, а в продольном и поперечном направлении имеет значения µяx и µяy.
6. Магнитное поле в боковой зоне полностью замыкается по бесконечно длинным расчетным шунтирующим участкам. Магнитная проницаемость шунтирующих участков по оси Z равна бесконечности, а по направлению осей X и Y определяются из условия, чтобы магнитное поле в боковых зонах было близким к реальному [5].
µ′x = µ0 /(α·hя), µ′y = µ0 (1 + hп/hя),
где α = π/τ;
hп, hя – высота паза и ярма индуктора;
τ – длина полюсного деления.
При таком допущении магнитное поле боковых зон равномерно распределяется по высоте шунтирующих участков, что значительно упрощает расчеты. В расчетной модели различная ширина и смещение вторичного элемента относительно индуктора учитывается соответствующим изменением ширины и электропроводности зон (2–5).
Согласно принятым допущениям среда во всех зонах расчетной модели является магнито-анизотропной. На базе основных уравнений электромагнитного поля, используя граничные условия между зазором и индуктором, получены дифференциальные уравнения векторного потенциала в проводящей среде зазора с учётом анизотропных магнитных свойств ярма и скалярного потенциала электрического поля [5].
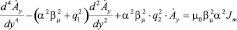, (1)
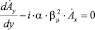, (2)
где
; 
; 
; 
.
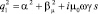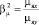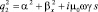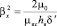Решения уравнений (1) и (2) для составляющих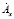 
, 
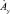в виде табулированных функций комплексного аргумента.
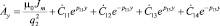, (3)
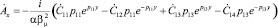, (4)
где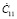 
, 
, 
, 
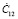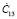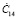– постоянные интегрирования;
p11, p13 – корни характеристического уровня.
Уравнения (1) и (2) описывают электромагнитное поле в электропроводящих зонах (2–5) расчетной модели. В зонах 1 и 6 проводящая среда отсутствует и скалярный потенциал φ равен нулю, поэтому в этих зонах электромагнитное поле описывается более простыми уравнениями.
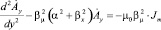. (5)
Решение уравнения
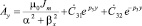, (6)
где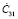 
, 
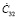– постоянные интегрирования;
p3 – корень характеристического уравнения.
Значение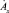 
находят из (2).
Постоянные интегрирования определялись из граничных уравнений. В качестве граничных условий использовались равенства касательных составляющих векторного потенциала, напряженности электрических и магнитных полей, а также условие непрерывности индуцированного тока в проводящей среде.
, 
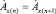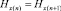, (7)
, 
,
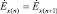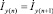где (n) и (n + 1) – номера соседних зон.
Параметры электромагнитного поля и интегральные характеристики ДЛАД достаточно просто определяются через потенциалы поля.
Магнитная индукция в зазоре
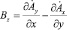. (8)
Напряженность электрического поля вторичного элемента
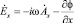; (9)
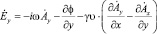. (10)
Ток, индуцированный во вторичном элементе
, 
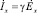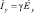. (11)
Электромагнитная мощность
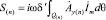. (12)
Тяговое усилие
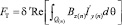, (13)
где Q(n) – площадь зоны n.
Электромагнитное поле, мощности и тяговое усилие при поперечном смещении вторичного элемента рассчитываются по выражениям (8–13), а поперечные усилия в электропроводящих зонах (2–5) определяются по формуле
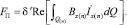(14)
Результирующее поперечное усилие, действующее на вторичный элемент, равно сумме поперечных усилий этих зон.
По полученным выражениям была составлена программа расчета характеристик ДЛАД при поперечном смещении вторичного элемента, реализованная на ЭВМ.
Расчетные тяговые и поперечные усилия приведены на рис. 3, откуда следует, что при увеличении поперечного смещения тяговое усилие монотонно уменьшается, а поперечное усилие вначале увеличивается, достигая своего максимального значения, а затем уменьшается. Максимальное поперечное усилие возникает при входе края вторичного элемента в зону индуктора и достигает порядка 50 % от максимального тягового усилия при симметричном положении вторичного элемента.
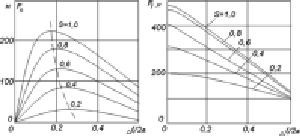
Рис. 3. Расчетные тяговые (Fт) и поперечные (Fп) усилия ДЛАД при поперечном смещении вторичного элемента
Для оценки точности разработанного метода расчета были выполнены экспериментальные исследования на круговом асинхронном двигателе. В качестве вторичного элемента использовался шихтованный ротор, покрытый медной лентой. При этом предусматривалась возможность смещения проводящей ленты в поперечном направлении относительно индуктора.
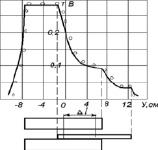
Рис. 4. Распределение индукции по ширине двигателя (Δl = 0,052 м): непрерывной линией – расчет, кружками – экспериментальные точки
На рис. 4 показано положение проводящей ленты относительно индуктора и приведены экспериментальные и расчетные значения магнитной индукции в зазоре и в боковых зонах. Согласно этому рисунку поперечное смещение проводящей ленты приводит к значительной асимметрии распределения магнитной индукции по ширине двигателя. При этом на правом краю индуктора наблюдается значительное уменьшение магнитной индукции за счет размагничивающего действия индуцированных во вторичном элементе токов.
На рис. 5 представлены расчетные и экспериментальные характеристики двигателя при поперечном смещении проводящей ленты. Расчетные зависимости изображены сплошными линиями, экспериментальные – точками.
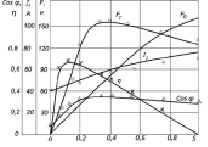
Рис. 5. Характеристики двигателя при Δl = 0,052 м
Сопоставление результатов расчёта и эксперимента позволяет сделать вывод об удовлетворительной точности расчёта характеристик двигателя при поперечном смещении вторичного элемента.
Результаты проведенных исследований были использованы при проектировании линейных и дугостаторных асинхронных двигателей для транспортных систем общепромышленного и специального назначения, а также при создании тихоходного двигателя для электропривода станков-качалок в нефтяной промышленности.
Работа выполнена в ФГБОУ ВО ПНИПУ при финансовой поддержке Министерства образования и науки РФ (договор № 02.G25.310068 от 23.05.2013 г. в составе мероприятия по реализации постановления Правительства РФ № 218).