Динамика пропорционально-интегрально-дифференциального (ПИД) регулирования (рисунок 1, [2, 6, 10]) описывается континуальной моделью:
. (*)
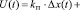
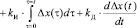При одинаковых настроечных параметрах и различном дискретном представлении интеграла в континуальной модели (*) (по формуле прямоугольника – Модель П, по формуле трапеции – Модель Т, по формуле Симпсона – Модель С) [7, 8] динамика регулируемого параметра показывает различные результаты [2, 7]. Эксперименты показали [2, 7, 8], что для разных настроечных параметров и разных моделей объекта регулирования заранее нельзя указать модель цифрового регулятора, обеспечивающую наилучшие динамические показатели, хотя бы потому, что перенос результатов синтеза аналоговых регуляторов на цифровую аппаратуру не гарантирует спроектированные показатели качества динамики регулируемого параметра, а замена континуальной модели регулирования на дискретную модель в конкретном программном обеспечении и программном ресурсе используемых процессоров не гарантирует достижение требуемых показателей устойчивости.
Все это делает актуальным создание программных средств либо по доведению дискретной модели регулирования до вида, обеспечивающего требуемую (аналоговую) динамику, либо по выбору требуемых методов и алгоритмов по достижению заданных целей регулирования.
В последние годы представлены системы моделирования, посредством которых можно было бы оценить настроечные параметры и отобразить изменение регулируемых параметров [9]. По эффективности их применения выделяются: «Программа для управления и исследования регулируемых систем электропривода в среде CX – Supervisor» (В.С. Климаш, М.А. Соколовский – ФГБОУ ВПО КнАГТУ, Свидетельство о гос. регистрации программ для ЭВМ № 2012618660, 2012); «Программа имитационного моделирования гибридной адаптивно-робастной системы управления нелинейными объектами периодического действия» (Е.Л. Еремин, Б.Н. Лелянов, Е.А. Шеленок – ФГБОУ ВПО ТОГУ, Свидетельство о гос. регистрации программ для ЭВМ № 2013661057, 2013); «Программа имитационного моделирования гибридной адаптивно-робастной системы управления нелинейными периодическими объектами с запаздыванием» (Е.Л. Еремин, Б.Н. Лелянов, Е.А. Шеленок – ФГБОУ ВПО ТОГУ, Свидетельство о гос. регистрации программ для ЭВМ № 2013661060, 2013); «Программный комплекс «Синтез и анализ цифровых систем управления (Sintez&Analiz)» (В.П. Казанцев, А.Б. Петроченков, Д.А. Даденков – ФГБОУ ВПО ПНИПУ, Свидетельство о гос. регистрации программ для ЭВМ № 2013660457, 2013); «MexBIOS Development Studio – система автоматизированного проектирования цифровых устройств управления» (А.С. Каракулов, В.С. Саидов, С.В. Ляпушкин, Н.В. Гусев, М.В. Сливенко, Г.В. Родионов – ООО «Научно-производственная фирма Мехатроника-Про», Свидетельство о гос. регистрации программ для ЭВМ № 2013617346, 2013); «Программа управления электронно-цифровым регулятором» (ООО НОЦ «ЛЕММА», Свидетельство о гос. регистрации программ для ЭВМ № 2014616405, 2014); «Исследование процесса настройки параметров типовых регуляторов с использованием непараметрической модели» (А.В. Банникова, Н.А. Сергеева – ФГАОУ ВПО СФУ, Свидетельство о гос. регистрации программ для ЭВМ № 2014616687, 2014); «Параметрическая оптимизация системы с ПИД-регулятором по различным критериям качества при помощи генетического алгоритма» (Н.Н. Куцый, Н.Д. Лукьянов – ФГБОУ ВПО ИрГТУ, Свидетельство о гос. регистрации программ для ЭВМ № 2014611433, 2014); «Программа для промышленного технологического ПИД-регулятора температуры» (Е.Н. Тумаев, Я.П. Иванов – ФГБОУ ВПО КубГУ, Свидетельство о гос. регистрации программ для ЭВМ № 2015616303, 2015); «Модель электропоезда «Сапсан» в режиме тяги» (А.М. Евстафьев, Д.В. Пегов, А.Н. Сычугов – ФГБОУ ВПО ПГУПС, Свидетельство о гос. регистрации программ для ЭВМ № 2015614389, 2015); «Имитационная модель цифровой системы управления скоростью движения асфальтоукладчика» (В.И. Иванчура, А.П. Прокопьев, Н.Н. Зуйкова – ФГАОУ ВПО СФУ, Свидетельство о гос. регистрации программ для ЭВМ № 2016611927, 2016); «Имитационная модель цифровой системы управления подачей и распределением смеси асфальтоукладчиком» (В.И. Иванчура, А.П. Прокопьев, Н.В. Кныш – ФГАОУ ВПО СФУ, Свидетельство о гос. регистрации программ для ЭВМ № 2016611878, 2016); «Имитационная модель цифровой следящей системы управления нивелированием выглаживающей плиты асфальтоукладчика» (В.И. Иванчура, А.П. Прокопьев, А.П. Машукова – ФГАОУ ВПО СФУ, Свидетельство о гос. регистрации программ для ЭВМ № 2016611928, 2016); «Имитационная модель цифровой адаптивной системы управления рабочим органом асфальтоукладчика» (В.И. Иванчура, А.П. Прокопьев, Е.В. Говоруха – ФГАОУ ВПО СФУ, Свидетельство о гос. регистрации программ для ЭВМ № 2016611928, 2016); «Программа имитационного моделирования систем автоматического управления котлоагрегата ТЭЦ» (Е.В. Боголей, И.В. Боголей, Д.А. Теличенко – ФГБОУ ВПО АмГУ, Свидетельство о гос. регистрации программ для ЭВМ № 2016611190, 2016).
Однако общим ограничением отмеченных программных средств является то, что они не позволяют, во-первых, моделировать и одновременно наблюдать динамику по разным дискретным моделям с целью оценки эффективности и выбора подходящей дискретной модели и, во-вторых, конструировать модель или алгоритм регулирования, подходящий или даже наилучший для конкретных параметров схемы цифрового регулирования.
А это уже указывает на актуальность создания не столько программных средств моделирования процессов цифрового регулирования, сколько на актуальность решения вопросов проектирования программного инструментария по моделированию методов и алгоритмов цифрового регулирования.
В работе предложены программные средства для организации одновременного моделирования и отображения процессов изменения регулируемых параметров по разным дискретным моделям цифрового регулирования с целью получения наилучшей модели.
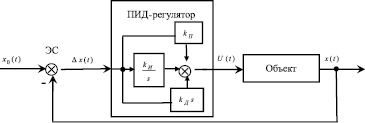
Рис. 1. Замкнутый контур регулирования по отклонению [8]: x0(t) – задающее воздействие (уставка); Δx(t) – рассогласование в текущий момент (невязка, отклонение, ошибка); U(t) – управляющее воздействие; x(t) – регулируемая величина; ЭС – элемент сравнения (Δx(t) пропорционален x0(t) – x(t)); kП, kИ и kД – настроечные параметры регулятора; оператор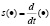 
(t = n·T, где: n = 0, 1, 2, …; T – время дискретизации)
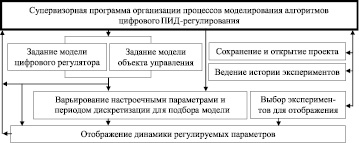
Рис. 2. Функционал инструментария моделирования алгоритмов цифрового ПИД-регулирования
Программный инструментарий. Структура цепи регулирования (рис. 1) фактически обуславливает своими компонентами программные средства задания модели цифрового ПИД-регулятора, модели объекта управления (ОУ), а также программного средства, обеспечивающего требуемое отображение динамики регулируемого параметра. Для модели регулятора инструментарий должен обеспечивать выбор математической модели (Модель П, Модель Т, Модель С); задание периода дискретизации Т (t = n·T, где n = 0, 1, 2, …), вида уставки (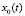
) и значений настроечных параметров kП, kИ и kД. Для модели объекта управления инструментарий должен касаться задания параметров модели, например в случае токового контура двигателя постоянного тока – это параметры а и b (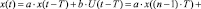
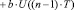. Программный инструментарий для организации процессов отображения должен ориентироваться на вывод кривых и табличных данных результатов моделирования, что позволит оперативно оценить и подобрать модель цифрового регулирования. Причём здесь основным требованием выступает потребность одновременной фиксации и наблюдения динамики регулируемых параметров по нескольким моделям, что, в свою очередь, требует наличия программных средств ведения истории (добавление, удаление экспериментов, очистка истории) и выбора отображаемых экспериментов. Кроме того, нельзя не учитывать потребность в инструментах варьирования настроечных параметров и времени дискретизации для оценки и выбора подходящей цифровой модели ПИД- регулятора.
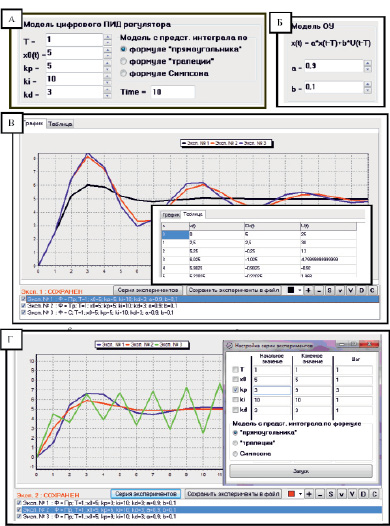
Рис. 3. Пример работы программного инструментария: A) задание модели цифрового регулятора; Б) задание модели ОУ (для случая а = 0,9, b = 0,1); B) отображение динамики регулируемых параметров, ведение истории и выбор отображаемых экспериментов; Г) варьирование настроечными параметрами и периодом дискретизации
Исходя из опыта создания программных систем ПИД-регулирования [1, 3, 4], основа структуры программной системы по реализации требуемого инструментария выражается функционалом (рис. 2).
Программные возможности инструментария. Реализация функционала (рис. 2) системой моделирования [5] показала эффектные возможности инструментария:
1) по заданию моделей (рис. 3, А, Б);
2) по оперативному выбору и организации различных сочетаний одновременного регулирования по дискретным моделям на основе замены интеграла в континуальной модели по формуле прямоугольника, трапеции и Симпсона (рис. 3, В);
3) по варьированию настроечных параметров и периода дискретизации для подбора подходящей модели цифрового регулятора (рис. 3, Г);
4) по оперативному расширению используемых дискретных моделей и организации процессов регулирования на их основе.
Полученные результаты: предложенная структура программных инструментальных средств моделирования алгоритмов цифрового ПИД-регулирования, исходя из необходимости реализации дискретного представления континуальной модели заменой в ней интеграла по формулам прямоугольника, трапеции и Симпсона, отличается средствами организации одновременного отображения динамики регулируемых параметров при использовании различных моделей цифрового регулирования и выбором наилучшей модели.
Исследование выполнено при поддержке «ОГУ имени И.С. Тургенева» по теме «Разработка программной системы поддержки процесса управления в предаварийных состояниях для восстановления нормальной работы», приказ № 7-н/26 от 23.10.2013 г.