Современная виртуальная образовательная среда – это быстроразвивающаяся, многоуровневая и многофункциональная система, объединяющая педагогические, дидактические и методические технологии; информационные ресурсы, включая базы данных и знаний, электронные учебные материалы и т.д.; современные программные средства, включающие программные оболочки и средства электронной коммуникации. В качестве компонента такой среды могут выступать различные тестирующие приложения, программы-тренажеры, в т.ч. использующие различные передовые технологии, такие как трехмерная компьютерная графика, беспроводные коммуникации, мобильные программно-аппаратные платформы. Значительная часть таких приложений используют различные стратегии адаптации к пользователю, проходящему обучение. Однако в ряде случаев может быть необходимо определение многоконтурных обратных связей, обеспечивающих возможность адаптации по ряду различных показателей. Для реализации возможности эффективного и быстрого определения таких обратных связей необходима разработка соответствующей математической модели.
Структура адаптивной обучающей программы в формате модели характеристик
В качестве основного инструмента при создании математической модели предлагается использовать методы морфологического анализа и синтеза. Данные методы широко применяются в инженерной практике для моделирования сложных систем в условиях, когда выбор оптимальной структуры осложняется неопределенностями поведения и состояния окружающей среды [1].
Результатом выполнения морфологического анализа является морфологическое множество, называемое также множеством альтернатив, содержащим в себе описание всех возможных вариантов системы. В процессе морфологического синтеза осуществляется поиск на морфологическом множестве оптимальной структуры синтезируемого объекта.
Наиболее часто для проведения процедур морфологического анализа и синтеза используются И/ИЛИ-деревья. Одной из основных сфер применения описанных подходов является разработка различных технических систем.
Основная идея подхода, предлагаемого в данной работе, заключается в применении методов морфологического анализа и синтеза для разработки математического и алгоритмического обеспечения адаптивных обучающих программ, являющихся компонентами виртуальной образовательной среды. В данном случае предлагается использовать морфологическое множество не для синтеза конечных вариантов системы (как в случае с техническими системами), а для определения отдельных состояний функционирования одной программной системы. Адаптивность такой системы будет заключаться в том числе и в возможности синтеза состояний в процессе выполнения программы.
Основные компоненты программы и взаимосвязи между ними при использовании предлагаемого подхода будут описываться как морфологическое множество. Данное морфологическое множество будем называть общей структурой программы. Для моделирования общей структуры будем использовать не стандартные И/ИЛИ-деревья, а модели характеристик [2, 3]. Модель характеристик (или диаграмма характеристик) представляет собой усовершенствованное И/ИЛИ-дерево, в котором, помимо стандартных отношений между вершинами по типу И/ИЛИ, предусмотрены также отношения множественного ИЛИ, обязательного включения дочерней вершины, произвольного включения дочерней вершины, а также отношения, связывающие между собой вершины не являющиеся дочерними или родительскими по отношению друг к другу (отношение требования посторонней вершины и отношение исключения посторонней вершины).
Для задания морфологического множества разработчик должен определить общую структуру программы в формате диаграммы характеристик. Конкретные же состояния работы программы будут определяться по диаграмме характеристик как вручную пользователем, так и автоматически в процессе выполнения на основе имеющихся обратных связей.
Процедура морфологического анализа будет включать в себя следующие шаги:
1) определение классов объектов обучающего программного приложения;
2) выделение классификационных признаков объектов;
3) определение значений выделенных классификационных признаков;
4) объединение выделенных классов и признаков в единую систему для последующего проведения процедуры синтеза.
Результатом выполнения приведенных действий будет морфологическое множество, определенное в формате диаграммы характеристик.
Задача синтеза в таком случае сводится к оптимальному выбору по составленной диаграмме набора вершин, характеризующего отдельное состояние функционирования системы.
Общая структура типовой обучающей программы представлена на рис. 1. Общая структура, описываемая с помощью модели характеристик, будет включать следующие основные категории объектов:
1) модели,
2) программные функции,
3) параметры.
Основной единицей изменчивости в данном случае будет выступать конфигурация диаграммы характеристик. Под конфигурацией диаграммы характеристик следует понимать отдельное подмножество ее элементов, удовлетворяющее условиям, налагаемым связями между вершинами. Так как диаграмма в целом является описанием всего пространства возможных состояний программы, то ее конфигурация будет использоваться в качестве описания отдельного состояния.
Для обеспечения дальнейшей работы с полученной структурой программы требуется ее преобразование в теоретико-множественное представление.
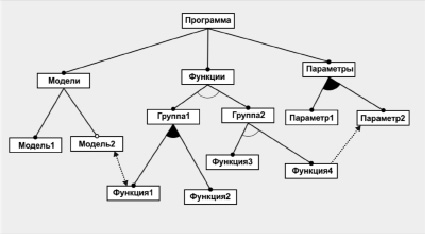
Рис. 1. Общая структура типовой адаптивной обучающей программы
Теоретико-множественное представление общей структуры адаптивной обучающей программы
В качестве альтернативной формы представления диаграммы характеристик был выбран ориентированный гиперграф.
Рассмотрим необходимые определения. Под ориентированным гиперграфом H (или просто гиперграфом) будем понимать упорядоченную пару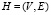 
, которая включает следующие элементы:
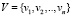– конечное множество вершин (узлов) гиперграфа;
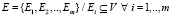– множество упорядоченных гиперребер;
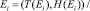
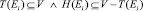– ориентированное гиперребро, для которого T(Ei) – хвостовое множество и H(Ei) – головное множество.
Под хвостовым множеством гиперребра понимается множество вершин, из которых «исходит» гиперребро, под головным множеством – множество вершин, в которые «входит» гиперребро. Именно порядок следования данных множеств определяет ориентацию гиперребра.
Перейдем теперь к преобразованию диаграммы характеристик в форму ориентированного гиперграфа. При данном преобразовании к основным элементам модели характеристик будут применяться следующие правила [4]:
Множество характеристик модели будет отображено на множество вершин соответствующего гиперграфа Features > V.
Множество взаимоотношений модели будет отображено на множество гиперребер, соединяющих вершины гиперграфа (характеристики модели) Relations > E.
Основные типы взаимоотношений модели характеристик будут иметь следующие аналогии в гиперграфовой форме:
1. Отношение основной дочерней характеристики является гиперребром E = (TE, HE), так что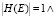 
маркировка (Е) = [1…1].
2. Отношение опциональной дочерней характеристики является гиперребром E = (TE, HE), так что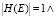 
маркировка (Е) = [0…1].
3. Взаимоотношение выбора (исключающее ИЛИ, XOR) является гиперребром E = (TE, HE), так что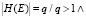 
маркировка (Е) = [1…1].
4. Взаимоотношение множественного выбора (ИЛИ, OR) является гиперребром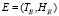 
, так что 
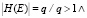маркировка (Е) = [m…n], 1 ≤ m ≤ n ≤ q.
5. Отношение включения является гиперребром E = (TE, HE), так что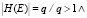 
маркировка (Е) = [q…q].
6. Отношение исключения является гиперребром E = (TE, HE), так что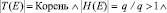 
маркировка (Е) = [0…1].
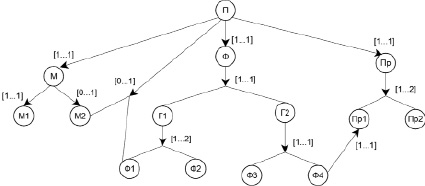
Рис. 2. Гиперграфовое представление диаграммы характеристик
Формально модель характеристик представляет собой ориентированный прямой гиперграф (или F-граф)
, (*)
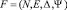где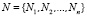 
– конечное множество вершин графа (характеристик исходной модели);
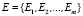– конечное множество ребер графа (взаимоотношений исходной модели);
– корневая вершина графа (корневая характеристика модели);
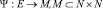– функция маркировки, присваивающая значение мощности 
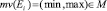, где M – множество значений мощности диаграммы, N – множество вершин гиперграфа, каждому ребру Ei, так что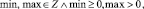 
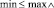
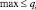, где Z – множество целых чисел.
Под значением мощности понимается минимальное и максимальное количество вершин из головного множества гиперребра, которые могут быть включены в конфигурацию описываемой гиперграфом модели характеристик (подграф исходного гиперграфа).
Корневая вершина 
является единственной вершиной гиперграфа, которая не принадлежит ни одному головному множеству ни одного гиперребра. По отношению к корневой вершине и множеству R, содержащему данную вершину, также справедливы следующие правила [5, 6, 7]:
1) 
};
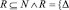2) BS(Δ) = 0;
3) 
.
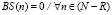На рис. 2 представлен гиперграф, соответствующий диаграмме характеристик, изображенной на рис. 1.
Преобразование общей структуры программы в гиперграфовую форму позволит провести ее дальнейший теоретико-множественный анализ (например, верификацию), а также алгоритмизировать процесс ее адаптивного поведения.
Математическая модель изменчивости адаптивной обучающей программы
Требуемая математическая модель должна обеспечивать возможность алгоритмизации основных процессов изменчивости без перекомпиляции исходного кода. Такая модель должна настраиваться пользователем под нужды предметной области (т.е. из общей абстрактной модели преобразовываться в уточненную модель), и на основе полученной уточненной модели должна производиться настройка алгоритма, реализующего процесс адаптивного поведения системы. Свойство инвариантности к предметной области возможно обеспечить за счет корректного использования модели морфологического множества программы.
С учетом приведенных требований предлагается следующая математическая модель:
,
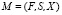где F – представление общей структуры приложения в форме ориентированного гиперграфа, полученного на основе диаграммы характеристик и описываемого формулой (*);
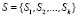– конечное множество конфигураций диаграммы характеристик, каждая из которых является описанием определенного состояния адаптивной системы (подграфом исходного гиперграфа);
X – матрица переходов между состояниями программы.
Пример матрицы переходов
|
Строки |
Столбцы |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
[0; 0,5) |
[0,5; 2) |
[2; ∞) |
Ø |
Ø |
|
2 |
Ø |
[0; 0,5) |
[0,5; 2) |
[2; 5) |
[5; ∞) |
|
3 |
Ø |
[0; 0,1) |
[0,1; 0,5) |
[0,5; 4) |
[4; ∞) |
|
4 |
Ø |
Ø |
[0; 0,1) |
[0,1; 0,7) |
[0,7; ∞) |
|
5 |
Ø |
Ø |
Ø |
Ø |
[0; 1) |
Матрица содержит элементы xij, каждый из которых представляет собой интервал [a; b) либо пустое множество
Ø, причем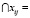 
Ø и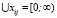 
, j = 1…k, i – фиксировано. Из состояния p осуществляется переход в состояние q, если показатель работы пользователя с программой 
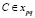. Если 
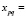Ø, то переход из состояния p в состояние q невозможен.
Пример матрицы переходов представлен в таблице.
Чтобы с помощью описанной модели произвести синтез адаптивной системы, необходимо:
1. Описать общую структуру программы в форме диаграммы характеристик.
2. Определить отдельные состояния работы программы как подмножества характеристик исходной диаграммы.
3. Задать связь между состояниями в формате матрицы переходов.
Как видно, предложенная математическая модель изменчивости является достаточно наглядным и удобным инструментом синтеза структуры адаптивной программной системы. Элементы данной модели служат для описания пространства возможных состояний программы.
Заключение
В данной работе впервые предложена математическая модель изменчивости компьютерных обучающих программ, основанная на теоретико-множественном представлении объектов характеристического моделирования. В основе построения данной модели лежат принципы морфологического анализа и синтеза. Модель позволяет определять многоконтурные обратные связи в адаптивной обучающей программе, а также создавать отдельные состояния работы приложения не только в процессе проектирования, но и в процессе выполнения программы.