Правомерность и целесообразность применения аппарата теории массового обслуживания для моделирования и исследования работы устройств беспроводного доступа в интернет (УБДИ) была обоснована в [2, 6]. Там же показана возможность использования полученных результатов для администрирования и рассмотрены примеры задач управления работой УБДИ в предположении, что как входной поток пользователей, так и поток обслуживания обладают свойством ординарности. В работах [1, 5] построена математическая модель функционирования УБДИ в условиях группового обслуживания и сформулированы общие принципы администрирования смешанными потоками.
Поскольку профессиональная деятельность авторов связана с высшей школой, их прежде всего интересуют вопросы, связанные с использованием УБДИ в организации учебного процесса, в частности проведения компьютерного тестирования. Этот метод проверки качества усвоения изучаемого материала широко используется в Казанском технологическом университете и ряде других образовательных учреждений и, при наличии представительной базы тестовых вопросов на полноту и целостность, позволяет получить надежные аттестационные характеристики испытуемых [4, 7].
Рассмотрим порядок применения УБДИ при проведении тестовых испытаний. В момент времени t0 = 0 группа тестируемых студентов в количестве равном числу компьютеров в аудитории, которые могут быть подключены к сети Internet, получает доступ к базе заданий и приступает к тестированию. Студенты, давшие ответы на весь комплекс вопросов, отключаются от сети и их место занимают другие тестируемые в порядке живой очереди. Для каждого вида тестов устанавливается предельное время выполнения заданий T, по истечении которого испытуемый отключается от сети принудительно, независимо от показанного результата. Величина T устанавливается администратором в зависимости от сложности и числа предлагаемых заданий и, как правило, выбирается так, чтобы средний студент мог ответить на все вопросы и успешно завершить тестирование за время 0,7–0,8T.
Данное описание процедуры тестирования позволяет сделать замечания, важные для построения математической модели.
1. Поступление заявок в очередь происходит вполне традиционным образом, поэтому нет никаких оснований отказываться от гипотезы пуассоновского потока для описания процесса формирования очереди.
2. Поток обслуживания является смешанным, поскольку испытуемые могут заканчивать тестирование как в различные моменты времени, так и в составе небольшой группы, например в моменты времени кратные T, в случаях принудительного отключения от сети. График функции распределения плотности вероятности g(t) такого потока имеет вид, представленный на рис. 1, где tl – время выполнения тестовых заданий экспертом.
Это распределение обладает заметной отрицательной асимметрией и ненулевым эксцессом, а значит, аналитический вид функции распределения следует искать в самом общем виде как решение дифференциального уравнения
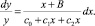(1)
Формулы для вычисления констант, входящих в состав этого уравнения, указаны Митропольским [7]:
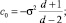
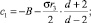
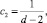(2)
где
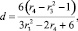
а r3 и r4 – основные моменты распределения третьего и четвертого порядка соответственно.
Таким образом семейство кривых (1) полностью определяется посредством первых четырех моментов.
Решение уравнения (1) известно и может быть представлено в виде
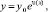(3)
где
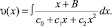
То есть вид решения зависит от коэффициентов квадратного трехчлена в знаменателе подынтегрального выражения.
Поместим начало координат в точку модального значения функции распределения t′, перейдя к новой координате z = t – t′. Это приведёт к смещению графика функции g(z) на t′ единиц влево с сохранением размаха распределения l = T – te.
Опустим технические детали и обратимся к результатам решения уравнения (1). Уравнение кривой, наиболее точно соответствующей наблюдаемому распределению, имеет вид
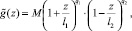(4)
где l1 = t′ – te; l2 = T – t′. И, поскольку положение точек l1 и l2 полагается известным, М – нормировочный коэффициент
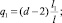
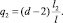
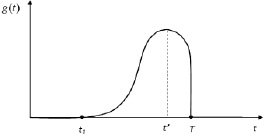
Рис. 1. Функция плотности вероятности потока обслуживания
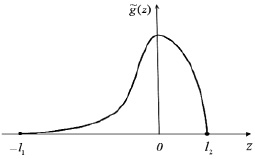
Рис. 2. График функции плотности распределения, соответствующий уравнению (4)
График этой зависимости представлен на рис. 2.
Очевидно, что чем меньше время te, тем заметнее будет проявляться асимметрия распределения.
Сравнение графиков, представленных на рис. 1 и 2, позволяет установить высокую степень соответствия зависимости, задаваемой уравнением (4), и функцией распределения времени выполнения студентами тестовых заданий. Отклонения вблизи точки t = T (z = l2), обусловленные принудительным отключением части тестируемых, вряд ли можно признать существенными.
Обратимся теперь к построению математической модели УБДИ как многоканальной системы массового обслуживания, используемой в процессе тестирования, выделив моменты, существенные для разработки алгоритма эффективного администрирования.
Во-первых, заметим, что отсутствие ограничения на количество мест в очереди и жестко определенное предельное время выполнения тестовых заданий исключает возможность возникновения поглощающего состояния. По этой же причине не имеет смысла и вопрос об относительной пропускной способности системы. Во-вторых, поскольку в нормальном режиме функционирования каждый освободившийся терминал сразу же занимается новым тестируемым, среднее число задействованных каналов практически равно числу разрешенных подключений. Таким образом, по сути дела единственной эксплуатационной характеристикой, представляющей интерес для решения задачи эффективного администрирования, которую важно оценить в ходе математического моделирования, является распределение времени ожидания обслуживания. Знание этой величины позволит составить удобный график проведения тестирования и поддерживать текущее количество ожидающих в очереди на приемлемом уровне.
Такая задача для одноканальной системы с пуассоновским входным потоком заявок и произвольным потоком обслуживания была решена Такачем [8]. Им было получено интегро-дифференциальное уравнение
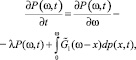(5)
где P(ω, t) – функция распределения времени ожидания ω в момент времени t; λ – интенсивность входного потока заявок;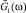 
– функция распределения времени обслуживания, плотность которого равна 
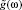. Он же указал решение этого уравнения в операторной форме для стационарного состояния
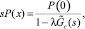(6)
где функции аргумента S есть изображения по Лапласу соответствующих оригиналов, а
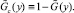
Опираясь на результат Такача, найдем вероятность ожидания обслуживания для стационарного состояния многоканальной системы с пуассоновским потоком накопления заявок в очереди и произвольным потоком обслуживания.
Рассмотрим систему массового обслуживания, имеющую в своем составе m параллельно работающих однотипных каналов с произвольным распределением времени обслуживания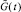 
и пуассоновским входным потоком заявок, интенсивность которого равна λ. Пусть в момент времени t один из каналов начал обслуживание заявки, а все остальные каналы в этот момент были заняты. Тогда вероятность того, что какой-либо из задействованных каналов, исключая тот, что был занят в момент времени t, не освободится через интервал времени z после начала обслуживания этой заявки, будет
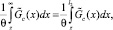
где θ – среднее время занятости канала, в нашем случае среднее время прохождения аттестации по всей совокупности тестируемых.
Отсюда следует, что вероятность W(z) занятости всех имеющихся каналов равна вероятности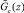 
(занятости канала, включившегося в работу в момент времени t, после момента z), умноженной на вероятность того, что и все остальные каналы останутся занятыми в течение времени превосходящего z,
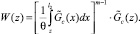(7)
Обращаясь к классическим образцам анализа подобных моделей, рассмотрим N однотипных многоканальных систем с одинаковым распределением потоков. В соответствии с введенными обозначениями количество систем, где время ожидания в очереди не превосходит ω, в момент времени t равно NP(ω, t), а количество систем, в которых время ожидания больше ω будет N – NP(ω, t). В момент времени t + Δt число систем первой группы изменится и станет равным NP(ω + Δt, t), за вычетом тех систем, которые имели время ожидания меньше или равное ω, но вследствие прихода заявок в течение интервала Δt перешли в другую группу.
Определим число систем, где время ожидания в момент времени t принадлежит интервалу x, x + dx. Дифференцируя P(x, t) по x, получим функцию плотности распределения времени ожидания и число искомых систем будет равно
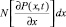
для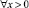 
и NP(0, t) для x = 0. Очевидно, что на интервале (t, t + Δt) время ожидания станет больше ω, если в течение времени Δt поступит одна заявка и если x + y > ω, где y имеет смысл времени, в течение которого это требование будет занимать канал, иначе говоря y > ω – x. Поэтому величину 
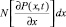надо умножить на вероятность прихода одной заявки за интервал Δt (поскольку поток пуассоновский, она будет равна λ•Δt) и на вероятность того, что длительность пребывания этой заявки на обслуживании превзойдет величину ω – x, которая равна W(ω – x).
Рассматривая случай x = 0, заметим, что нулевое время ожидания возможно только тогда, когда число заявок в системе не превосходит m – 1. Таких систем в момент времени t будет NP(0, t), однако перейти за время Δt в группу систем с ненулевым временем ожидания могут только те из них, где в момент времени t имеется ровно m – 1 заявок. Повторяя цепочку умозаключений, сделанную для случая x > 0, получим, что при x = 0 число систем, для которых на временном отрезке (t, t + Δt) время ожидания станет больше, ω определится как
где pm–1 – вероятность нахождения в системе ровно m – 1 заявок.
Объединяя полученные результаты, получим соотношение для расчета функции распределения времени ожидания в момент времени t + Δt
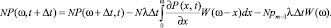
Разделив это соотношение на N и вычтя из его левой и правой части величину P(ω, t), разделим на Δt и, переходя к пределу при Δt → 0, имеем
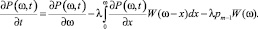(8)
Для стационарного состояния, когда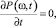 
выражение (8) принимает вид
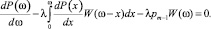(9)
Используя известные формулы преобразования Лапласа для производной, интеграла и свертки, легко получить изображение Лапласа функции P(ω)
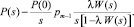(10)
Практическое применение этой формулы существенно ограничивает то обстоятельство, что величины P(0) и pm–1 неизвестны. Остановимся, однако, на одном из возможных способов использования полученного результата.
Разложим в ряд функцию W(s)
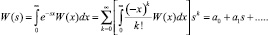
где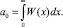 
Но, поскольку P(ω) есть функция распределения, то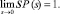 
Ограничиваясь вследствие малости S только первым членом разложения, получим из формулы (10)
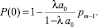(11)
Тем не менее единственным способом отыскания величины pm–1 остаётся имитационное моделирование.