Одним из наиболее сложных элементов современных энергетических систем является первичный двигатель электрических синхронных генераторов, которым обычно служит паровая турбина со своими системами регулирования. Основным способом получения информации, необходимой для проектирования, эксплуатации и развития электроэнергетических систем, является математическое моделирование [2]. Динамика первичных двигателей существенно влияет на нормальные и аварийные процессы производства, распределения и потребления электроэнергии. Поэтому требование к уровню адекватности модели первичного двигателя постоянно возрастает. А это означает, что на сегодняшний день описывать модели систем регулирования приходится в классе нелинейных систем.
Наиболее наглядной и исходной формой описания сложной динамической модели энергетической системы является структурная (операторная) схема, которая не только иллюстрирует содержание модели, но и показывает структуру моделируемых объектов, что позволяет легко ориентироваться в ней и адаптировать ее для конкретных целей. Поэтому актуальной является задача разработки алгоритмов синтеза систем регулирования, заданных структурной схемой.
Решение поставленной задачи осложнено тем, что в настоящее время в электроэнергетических системах находится в эксплуатации множество различных типов турбин и котлоагрегатов с разнообразными системами и законами регулирования. Хотя передаточные функции отдельных элементов и звеньев известны, разработка полной математической модели для конкретного типа оборудования и компоновки первичного двигателя, а также расчета системы регулирования является уникальной [2, 8, 9, 11]. Поэтому возникает задача разработки универсального алгоритма синтеза, который может использоваться для стационарных и нестационарных систем, как для линейных, так и нелинейных систем управления. Такие алгоритмы могут быть построены на использовании метода матричных операторов расчета и проектирования сложных систем [6, 13]. Для иллюстрации таких алгоритмов в работе приводится синтез системы регулирования турбины производства Калужского турбинного завода. Хотя модель не является громоздкой, но на ее примере довольно подробно иллюстрируются все особенности алгоритма, что не снижает его общности по отношению к системам высокого порядка [10].
Общий алгоритм синтеза системы регулирования
Рассмотрим систему регулирования турбины ПТ-25/30-90/10М производства Калужского турбинного завода в классе нелинейных систем (рис. 1) [7]. Эта система предназначена для поддержания частоты вращения ротора турбины на требуемом уровне.
На рис. 1 обозначено: φ – относительное отклонение угловой частоты вращения ротора от номинального значения ωНОМ,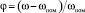 
; λ – относительное отклонение электрической нагрузки генератора; ξ – относительное изменение расхода пара в турбине; μ – относительное отклонение поршня сервомотора; z – относительное отклонение поршня золотника; δ – степень неравномерности системы регулирования; Tz – постоянная времени золотника; Tμ – постоянная времени сервомотора; Tξ – постоянная времени камеры эквивалентного объема (время полного заполнения камеры при определенном расходе пара); Tφ – постоянная времени ротора; θ – эквивалентный коэффициент самовыравнивания.
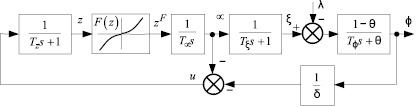
Рис. 1. Структурная схема нелинейной системы регулирования энергетической турбины ПТ-25/30-90/10М (ПТ-12/15-35/10М)
Нелинейность F(z), определяющая форму кромок отсечного золотника, описывается следующей зависимостью:
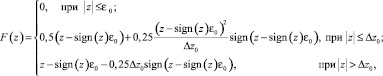
где Δz0 – относительные высоты треугольного профиля кромок поршня отсечного золотника; ε0 – величина, характеризующая степень нечувствительности сервомотора.
Требуется определить параметры системы регулирования δ, Tz, Tμ таким образом, чтобы φЭ(t) и φ(t) (реальный переходной процесс) были близки, например, в среднеквадратическом смысле:
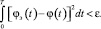
Представим модель системы регулирования турбины с нелинейностью в операторной форме (в матричном виде) (рис. 2).
На схеме обозначено:
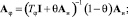
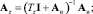
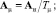
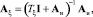
где AИ – матричный оператор интегрирования. Из рис. 2 имеем следующие векторно-матричные соотношения:
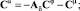
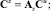
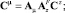
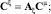
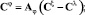
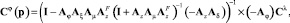
или
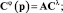
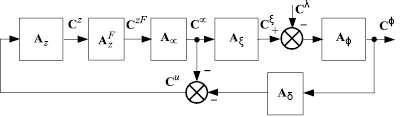
Рис. 2. Структурная схема нелинейной системы регулирования энергетической турбины в операторной форме
Последнее выражение представляет собой матричный оператор всей системы, который связывает спектральные характеристики входного и выходного процессов. Матричный оператор нелинейного элемента вычисляется по формуле [6]:
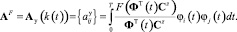(1)
Для вычисления спектральных характеристик остальных процессов системы нужно воспользоваться структурными преобразованиями. В результате можно получить следующие зависимости:
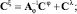
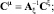
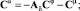
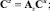
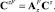
Алгоритм, определяющий процедуру решения задачи расчета параметров системы управления турбины, представлен на рис. 3.
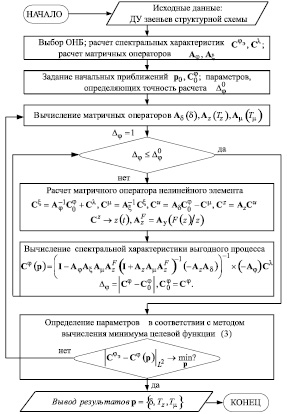
Рис. 3. Структурная схема алгоритма синтеза системы регулирования турбины в классе нелинейных систем
Вычислительный алгоритм синтеза системы регулирования первичного двигателя
Рассмотрим подробно алгоритм параметрического синтеза системы регулирования турбины ПТ-25/30-90, представленного на рис. 3.
Этап 1. При заданной структуре регулятора формируем вектор искомых параметров: p = [δ, Tz, Tμ]. Здесь же инициализируем вектор параметров начальными приближениями p0 = [1, 1, 1].
Этап 2. Накладываем ограничения на параметры, связанные с их физической реализуемостью. Эти ограничения будут пересланы в функцию оптимизации в качестве опции. Данная операция позволяет значительно сократить время поиска оптимальных параметров. Например, все полученные параметры регуляторов должны быть положительными.
Этап 3. Задаем эталонный переходный процесс при резком сбросе нагрузки (λ = –1):
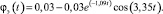
Стоит обратить особое внимание на то, чтобы эталонный переходный процесс соответствовал требованиям, предъявляемым в [12].
Этап 4. Выбор ортонормированного базиса на промежутке исследования [0, T]. В дальнейшем всегда будем использовать ортонормированный базис функций Уолша, упорядоченных по Адамару, и обозначать его H – квадратная симметричная матрица размера l×l. Вычисление спектральных характеристик входного и выходного воздействий.
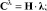
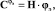
где λ, φЭ – вектор-столбцы отсчетов функций λ(t), φЭ(t) соответственно.
Этап 5. Определяем матричные операторы тех звеньев, параметры которых известны (как правило, это параметры объекта и часть параметров системы управления):
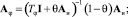
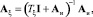
где AИ – матричный оператор интегрирования; I – единичная матрица; θ = 0,05 (коэффициент саморегулирования); для ПТ-25/30-90/10М: Tφ = 12 c, Tξ = 0,5 c. Эти матричные операторы, так же как и спектральные характеристики, рассчитываются один раз и хранятся в памяти ЭВМ.
Этап 6. Определяем матричные операторы звеньев, параметры которых подлежат определению (матричные операторы вычисляются при текущих значениях вектора искомых параметров p = [δ, Tz, Tμ]).
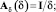
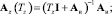
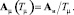
Здесь же можно задать начальное приближение для выходного сигнала (или его спектральной характеристики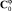 
).
Этап 7. Вычисление матричных операторов нелинейных звеньев. Для этого необходимо предварительно найти спектральные характеристики процессов на входе нелинейных элементов:
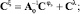
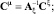
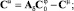
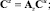z = HCz;
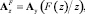
здесь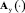 
– матричный оператор умножения функции представленной в скобках; z – вектор-столбец отсчетов функции z(t). Непосредственное применение формулы (1) для вычисления матричного оператора умножения является далеко не эффективным с точки зрения быстродействия его расчета. Так как система Matlab ориентирована на операции с матрицами, то для расчета матричного оператора умножения эффективно использовать следующую функцию:
function Ay=m_ymn1(H,f)
%Матричный оператор умножения на некоторую функцию %f – вектор-столбец
%H – матрица-базис функций Уолша
Ay=H*(H.*(ones(size(f))*f’)’);
Этап 8. Вычисление матричного оператора всей системы и спектральной характеристики выходного сигнала
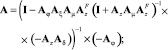
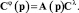
Этап 9. Уточнение матричных операторов нелинейных элементов. Для этого проверяем решения задачи анализа при текущих значениях p: степень близости спектральных характеристик выходного сигнала, полученных на текущей и предыдущей итерациях.
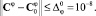(2)
Если (2) не выполняется, то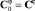 
, и переходим к этапу 7, если выполняется, то переходим к этапу 10.
Этап 10. Вычисление искомых параметров:
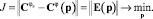(3)
Реализация (3) представляет собой итерационный процесс, в котором параметры меняются в соответствии с выбранным алгоритмом нахождения минимума функции многих переменных. При очередном вычислении целевой функции (3) при конкретных значениях p, следует определять Cφ(p), т.е. возвращаться к этапу 6. Если минимум найден, то переходим к анализу системы при найденных параметрах регулятора.
Этап 11. Анализ системы регулирования турбины при найденных параметрах регулятора:
φ = HCφ; z = HCz;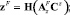 
μ = HCμ; ξ = HCξ,
где φ, 
z, μ , ξ – вектор-столбцы отсчетов функций φ(t),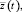 
z(t), μ(t), ξ(t) соответственно.
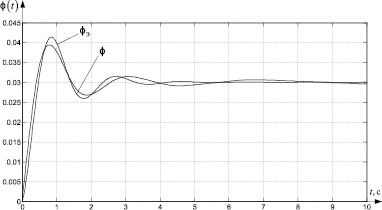
Рис. 4. Эталонный и реальный переходные процессы относительного изменения частоты вращения ротора
Результаты синтеза системы регулирования турбины ПТ-25/30-90/10М представлены на рис. 4 при λ = –1, ε0 = 0,0167. Размер базиса составлял 512 функций Уолша. В качестве меры близости спектральных характеристик в выражениях (2) и (3) использовалась евклидова норма. Минимизация целевой функции (3) осуществлялась методом Гаусса – Ньютона, который реализован в среде Matlab с помощью функции lsqnonlin. Эта функция позволяет осуществлять условную минимизацию целевых функций, представляющих собой свертку вектора.
Для системы регулирования турбины ПТ-25/30-90/10М были найдены следующие параметры (ограничения на параметры не накладывались):
δ = 0,03; Tz = 0,0630 с; Tμ = 0,1014 с; (4)
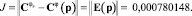
Для получения параметров (4) понадобилось 8 итераций. Степень нечувствительности сервомотора составляла ε0 = 0,0167, что соответствует 0,05 % нечувствительности системы регулирования относительно регулируемого процесса φ(t). В работах [1, 3, 4, 5, 14, 15] отражены детальные алгоритмы построения законов регулирования энергетических систем, в том числе и в робастной постановке, а также алгоритмы решения задач идентификации.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Калужской области (гранты № 14-48-03013, № 16-41-400701).