Компьютерное моделирование динамики механических систем широко используется в современной инженерной практике. Оно позволяет существенно уменьшить объём натурных испытаний и в конечном счёте сократить время и стоимость новых разработок. Требование точности компьютерного моделирования ведет к возрастанию сложности математических моделей технических систем. Но параллельно с ростом размерности математической модели увеличивается и трудоёмкость моделирования. Это отражается в серьезном росте времени, которое затрачивается на стадии оптимизации параметров проектируемой конструкции и исследовании ее поведения при различных условиях эксплуатации. Поэтому разработка методов, позволяющих ускорить процесс математического моделирования сложных технических систем, является актуальной задачей.
В настоящей работе выводится новая форма уравнений движения систем связанных твёрдых тел с использованием квазискоростей, обобщённых координат и обобщённых импульсов (импульсов Пуассона).
Описание механической системы. Матрица кинематической структуры
Рассмотрим систему абсолютно твёрдых тел со структурой дерева, соединенных шарнирами. Под шарнирами будем понимать соединение между двумя смежными телами, возникающее вследствие как наличия кинематической связи между телами, так и взаимодействия посредством различных силовых полей. Будем предполагать, что кинематические связи, реализуемые в шарнирах, голономны и идеальны.
Пусть N – число тел в системе (не считая тела «0», движение которого во времени относительно инерциальной системы координат (СК) Oxyz задано). Тогда количество шарниров всегда будет равно N, если учитывать шарнир между системой и телом «0».
Пронумеруем тела и шарниры системы, причем телам присвоим номера так, чтобы для любого тела в графе системы номер предшествующего ему тела был меньше, а шарниру, связывающему i-е тело с предшествующим, присвоим номер i. В этом случае для полного описания структуры взаимосвязей в такой системе достаточно одного целочисленного массива k = {k1, …, kN}, на i-м месте которого расположен индекс тела, предшествующего i-му. C каждым телом системы свяжем следующие множества: Pi – упорядоченное множество индексов шарниров, составляющих путь между нулевым и i-м телами; Ui – множество индексов шарниров, для которых i-е тело является предшествующим.
Положение и ориентацию i-го тела системы относительно инерциальной СК будем определять с помощью радиуса-вектора 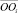 фиксированной на нём точки Oi и системы ортонормированных векторов
фиксированной на нём точки Oi и системы ортонормированных векторов 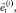
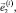
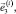 которые вместе с точкой Oi определяют СК Oixiyizi, неизменно связанную с i-м телом.
которые вместе с точкой Oi определяют СК Oixiyizi, неизменно связанную с i-м телом.
Введем следующие обозначения: 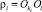 – матрица-столбец координат точки Oi в ki-й СК; ri = OOi – матрица-столбец координат точки Oi в инерциальной СК;
– матрица-столбец координат точки Oi в ki-й СК; ri = OOi – матрица-столбец координат точки Oi в инерциальной СК; 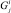 – матрица направляющих косинусов между базисными векторами
– матрица направляющих косинусов между базисными векторами 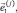
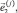
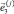 и
и 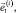
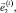
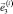 (матрица преобразования координат из j-й СК в i-ю).
(матрица преобразования координат из j-й СК в i-ю).
Предположим, что физическая связь в i-м шарнире моделируется системой li ≤ 6 идеальных голономных линейно-независимых связей. Тогда множество относительных положений i-го тела в ki-й СК образует ni-мерное конфигурационное многообразие [1], где ni = 6 – li. Уравнения этого многообразия можно записать в параметрической форме, введя матрицу-столбец 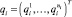 криволинейных (обобщенных) координат его текущей точки. Тогда матрицы ρi и
криволинейных (обобщенных) координат его текущей точки. Тогда матрицы ρi и 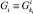 являются функциями обобщенных координат:
являются функциями обобщенных координат:
ρi = ρi(qi, t); Gi = Gi(qi, t).
Задание матрицы-столбца q = (q1, …, qN)T как функции времени позволяет однозначно определить взаимное положение всех тел и их движение относительно абсолютной системы координат в любой момент t.
Введенные матрицы связаны между собой рекуррентными формулами
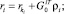
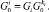
Принимая движение i-го тела за относительное, а предшествующего ему ki-го тела за переносное, в соответствии с правилом сложения скоростей можно записать рекуррентные формулы для вычисления проекций линейной νi и угловой ωi скоростей тел механической системы на оси i-й СК [8]:
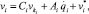 (1)
(1)
где
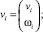
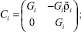
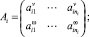
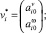
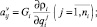
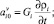
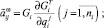
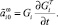
Здесь и далее символ «~» используется для обозначения кососимметричной матрицы (это соответствует матричной записи векторного произведения [8]).
Введём блочную 6N×6N-матрицу S с квадратными подматрицами порядка 6 по следующей формуле:
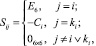
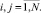 (2)
(2)
Заметим, что для любой кинематической структуры эта матрица содержит в каждой строке только два ненулевых блока E6 и –Ci. Поскольку матрица S содержит информацию как о топологической структуре системы, так и об относительном положении тел в системе, ее называют матрицей кинематической структуры. С использованием матрицы S уравнения кинематики системы тел (1) можно записать следующим образом:
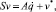 (3)
(3)
где v = (v1, ω1, …, vN, ωN)T, A = diag(A1, …, AN).
Рекуррентные формулы (3) можно записать в виде явных выражений
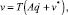 (4)
(4)
где обратная к S матрица T =S–1 является блочной 6N×6N-матрицей, подматрицы которой могут быть вычислены по рекуррентным формулам:
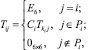
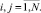 (5)
(5)
Для дальнейшего изложения нам потребуется соотношение для производной матрицы T. Для вывода этого соотношения получим формулу для производной матрицы Ci:
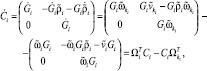
где введено обозначение
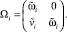
Из этого равенства и формулы (2) следует, что
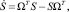 (6)
(6)
где Ω = diag(Ω1, …, ΩN).
Продифференцируем равенство ST = E и из полученного выражения выразим производную 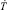 . Тогда с учётом формулы (6) получим
. Тогда с учётом формулы (6) получим
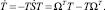 (7)
(7)
Расширенная система уравнений движения в импульсах Пуассона
Для составления уравнений движения систем связанных твёрдых тел со структурой дерева будем использовать принцип освобождения от связей. В этом случае мысленно уничтожаем связи между телами, а движение системы, осуществляемое при наличии связей, обеспечим введением дополнительных сил – реакциями связей. Введение этих реакций позволяет записать дифференциальные уравнения движения любого тела в форме уравнений Эйлера – Лагранжа для свободного твёрдого тела [8]:
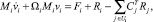 (8)
(8)
где
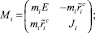
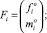
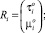
mi – масса i-го тела; Ji – тензор инерции i-го тела; 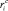 – матрица-столбец проекций радиуса-вектора центра масс i-го тела на оси связанной с ним СК;
– матрица-столбец проекций радиуса-вектора центра масс i-го тела на оси связанной с ним СК; 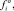
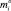 – проекции главного вектора и главного момента активных сил, действующих на i-е тело в i-й СК;
– проекции главного вектора и главного момента активных сил, действующих на i-е тело в i-й СК; 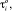
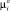 – проекции главного вектора и главного момента реакций связей в i-м шарнире в i-й СК.
– проекции главного вектора и главного момента реакций связей в i-м шарнире в i-й СК.
С использованием матрицы кинематической структуры S уравнение (8) запишем в краткой форме:
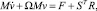 (9)
(9)
где
M = diag(M1, …, MN); F = (F1, …, FN)T;
R = (R1, …, RN)T.
Декартовым импульсом системы назовём 6N-мерную матрицу-столбец
pa = Mv. (10)
Тогда n-мерная матрица-столбец 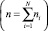
p = ATTTpa = BTpa
является обобщённым импульсом, или импульсом Пуассона [1].
Построим выражение для производной обобщённого импульса  . Для этого умножим слева на BT левую и правую части уравнения (9). Получим, что
. Для этого умножим слева на BT левую и правую части уравнения (9). Получим, что
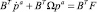
или
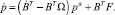 (11)
(11)
Здесь было учтено равенство
BTSTR = ATTTSTR = ATR = 0,
отражающее принцип идеальности связей. В уравнении (11) Q = BTF – матрица-столбец обобщенных сил.
Преобразуем выражение 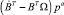 с учётом формулы (7):
с учётом формулы (7):
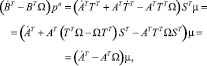
где введено обозначение μ = TT pa.
В результате получим следующую расширенную систему уравнений движения
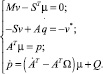 (12)
(12)
Особенность уравнений (12) состоит в том, что они разрешены относительно производных обобщённых импульсов  . Первые три из этих уравнений образуют линейную систему с симметричной, блочной трёхдиагональной разреженной матрицей коэффициентов относительно скоростей v,
. Первые три из этих уравнений образуют линейную систему с симметричной, блочной трёхдиагональной разреженной матрицей коэффициентов относительно скоростей v,  и переменных μ, которые являются множителями Лагранжа [4, 6]. Уравнения (12) для цепочки твердых тел впервые были выведены В.Н. Ивановым из принципа Гамильтона – Остроградского в работе [4]. В работе [6] эти уравнения были получены в координатной форме для систем твердых тел со структурой дерева.
и переменных μ, которые являются множителями Лагранжа [4, 6]. Уравнения (12) для цепочки твердых тел впервые были выведены В.Н. Ивановым из принципа Гамильтона – Остроградского в работе [4]. В работе [6] эти уравнения были получены в координатной форме для систем твердых тел со структурой дерева.
Структура первых трех кинематических уравнений системы (12) аналогична структуре расширенной системы уравнений динамики системы связанных твердых тел [5, 9, 10]:
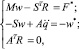 (13)
(13)
где w – матрица-столбец абсолютных линейных и угловых декартовых ускорений всех тел системы в связанных с ними СК. Правые части уравнений F* и w*, помимо внешних сил, содержат гироскопические, центробежные и явно зависящие от времени ускорения.
Отличие уравнений (12) и (13) состоит в том, что первые три уравнения системы (12) служат для получения значений обобщенных скоростей  , а не ускорений
, а не ускорений  .
.
Совпадение структуры уравнений (12) и (13) означает, что все разработанные ранее алгоритмы решения системы уравнений (13), такие как метод «прогонки» (отдельных тел) А.Ф. Верещагина [2, 3], методы проекций уравнений в подпространства обобщенных координат или подпространства линейно-независимых компонент реакций связей (схемы явного формирования уравнений движения в форме Лагранжа 2 или 1 рода) [7, 8, 11, 12], применимы и для системы уравнений (12).
Решение расширенной системы уравнений движения в импульсах Пуассона методом «прогонки»
Учитывая формулы (1) и (2), систему уравнений (12) запишем в следующем виде:
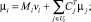 (14)
(14)
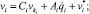 (15)
(15)
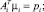 (16)
(16)
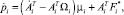 (17)
(17)
где
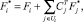
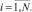 (18)
(18)
Построим на основе этой системы рекуррентные формулы для вычисления обобщённых скоростей  и множителей Лагранжа μi. Для этого сначала докажем, что для каждого тела системы множитель μi может быть представлен в виде
и множителей Лагранжа μi. Для этого сначала докажем, что для каждого тела системы множитель μi может быть представлен в виде
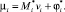 (19)
(19)
Нетрудно видеть, что для концевых тел системы такое представление наблюдается:
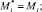
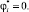
Предположим, что формула (19) справедлива для всех номеров j ∈ Si. Покажем, что она справедлива и для номера i. Для этого с помощью формулы (15) исключим из (19) матрицу-столбец vi:
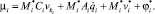 (20)
(20)
Подставим полученное равенство в уравнение (16) и выразим из него матрицу-столбец  :
:
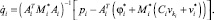 (21)
(21)
С помощью формул (20), (21) из уравнения (14) исключим множители μj, j ∈ Si, несомых тел:
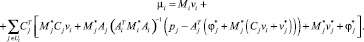
Собирая в полученном равенстве коэффициент перед vi, преобразуем его к виду (19), где
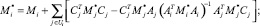 (22)
(22)
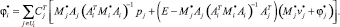 (23)
(23)
Таким образом, процесс вычисления обобщённых скоростей и производных обобщённых импульсов состоит из двух этапов. На первом из них по формулам (22), (23) и (18), начиная с концевых тел и заканчивая корневым, вычисляются матрицы 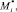
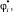
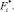 На втором этапе, начиная с корневого тела, с помощью формул (21), (15), (19) и (17) определяются обобщённые скорости
На втором этапе, начиная с корневого тела, с помощью формул (21), (15), (19) и (17) определяются обобщённые скорости  и производные обобщённых импульсов
и производные обобщённых импульсов 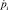 .
.
Данный метод является одним из самых эффективных методов численного моделирования систем с длинными кинематическими цепочками. Трудоёмкость решения системы уравнений (12) с помощью данного алгоритма растёт по линейному закону в зависимости от числа тел в механической систем [10]. При реализации этого алгоритма требуется обращение только матриц 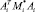 , порядок которых равен числу степеней свободы в i-м шарнире, причем эти матрицы симметричны и положительно определены, а их порядок всегда мал (не превышает шести). Именно этим и обусловлена эффективность представляемого метода.
, порядок которых равен числу степеней свободы в i-м шарнире, причем эти матрицы симметричны и положительно определены, а их порядок всегда мал (не превышает шести). Именно этим и обусловлена эффективность представляемого метода.
Описанный алгоритм аналогичен методу отдельных тел А.Ф. Верещагина, предложенному в работах [2, 3] для решения общих уравнений динамики цепочки твёрдых тел относительно ускорений.
Пример составления уравнений движения системы тел в импульсах Пуассона
Для иллюстрации техники составления уравнений (12), а также определения всех входящих в них параметров выведем уравнения движения для механической системы (элемента регулятора угловой скорости), изображённой на рисунке.
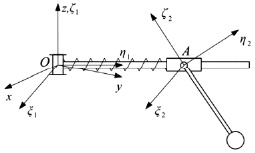
Введём неподвижную Oxyz и связанные с телами Oξ1η1ζ1, Oξ2η2ζ2 системы координат, как показано на рисунке. Система состоит из двух тел с массами m1 и m2 и осевыми моментами инерции J1x, J1y, J1z и J2x, J2y, J2z. Предположим, что:
а) в точке O цилиндрический шарнир обеспечивает вращение OA вокруг оси Oz;
б) точка A может перемещаться вдоль оси Oη1;
в) шарнир в этой точке обеспечивает вращение второго тела сначала вокруг оси Oη1, а затем вокруг оси Oξ2;
г) на тела системы действует сила тяжести;
д) точки O и A связаны пружиной.
Рассматриваемая система имеет четыре степени свободы. В качестве обобщённых координат выберем:
а) угол γ1 – угол поворота первого тела вокруг оси Oz;
б) изменяющуюся длину OA = y2;
в) углы β2 и α2 поворота второго тела вокруг осей Oη1 и Oξ2 соответственно, т.е. q1 = γ1; q2 = (y2, β2, α2)T, q = (y1, y2, β2, α2)T.
Подготовим элементы уравнений движения (12). Очевидно, что координаты точек O и A в системах координат Oxyz и Oξ1η1ζ1 соответственно равны
ρ1 = (0, 0, 0)T; ρ1 = (0, y2, 0)T.
Далее, матрицы направляющих косинусов между системами координат имеют вид
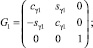
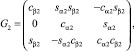
где
cγ1 = cos γ1; sγ1 = sin γ1; cα2 = cos α2;
sα2 = sin α2; cβ2 = cos β2; sβ2 = sin β2.
Масс-инерционные характеристики тел системы задаются матрицами
M = diag(M1, M2); rc1 = (0, yc1, 0)T;
rc2 = (0, 0, zc2)T,
где
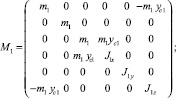
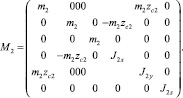
Кроме того, матрицы кинематической структуры и локальных касательных базисов конфигурационного многообразия возможных перемещений тел системы имеют вид
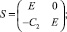 A = diag(A1, A2),
A = diag(A1, A2),
где
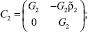
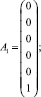

Отсюда производная матрицы A равна
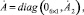
где
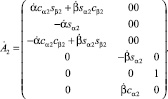
Вследствие того, что тело 0 системы стационарно, то вектор v* = 0. При этом вектор обобщённых сил имеет следующий вид:
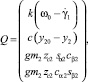
где ω0 = ω0(t) – заданная угловая скорость вращения первого тела; k – коэффициент усиления; c – коэффициент жёсткости пружины; y20 – длина ненапряжённого состояния пружины; g – ускорение свободного падения.
Теперь для получения уравнений движения в импульсах Пуассона достаточно подставить выписанные матрицы в уравнения (12).
Из анализа приведенного примера несложно установить, что объем информации, которую необходимо подготовить для построения математической модели системы твердых тел в форме уравнений (12), минимален.
Заключение
В работе получена новая расширенная матричная форма уравнений движения систем связанных твердых тел со структурой дерева. Уравнения содержат импульсы Пуассона, обобщенные координаты, квазискорости и множители Лагранжа. Они разрешены относительно производных импульсов Пуассона. Поэтому в отличие от классических уравнений в форме Лагранжа 1 или 2 рода представленные уравнения не требуется разрешать относительно старших производных (обобщенных ускорений) в процессе их численного интегрирования.
Построены рекуррентные формулы, предназначенные для автоматизированного компьютерного формирования уравнений движения систем связанных твердых тел из простейших основных блоков, описывающих структуру, масс-инерционные, геометрические и кинематические характеристики отдельных звеньев (тел и шарниров).
Для группы кинематических уравнений, входящих в расширенную систему уравнений, разработан матричный алгоритм разрешения относительно обобщенных скоростей, аналогичный известному методу «прогонки». Число арифметических операций в построенном алгоритме, как и в методе А.Ф. Верещагина [2, 3], растет линейно в зависимости от количества тел в механической системе. Поэтому для систем твердых тел с длинными кинематическими цепями разработанный алгоритм является более эффективным [10] в сравнении с процедурами моделирования, основанными на использовании уравнений в форме Лагранжа 2 рода, для которых аналогичная зависимость является кубической.



