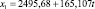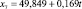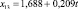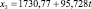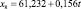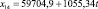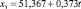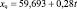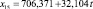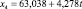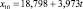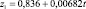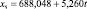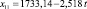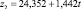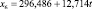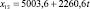Scientific journal

Fundamental research

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Железнодорожный транспорт является важнейшей отраслью страны, играет ключевую роль в её успешном развитии. Значительный интерес представляет получение так называемых дескриптивных прогнозных расчетов относительно будущих значений ключевых показателей функционирования транспортной отрасли. Именно к ключевым, несомненно, относятся показатели, связанные с грузовыми перевозками. Их прогнозированию и посвящена настоящая работа.

Краткое описание математической модели

В работе [6] представлена динамическая, нелинейная, открытая, рекурсивная математическая модель регрессионного типа для эксплуатационных показателей функционирования Красноярской железной дороги и факторов, на них влияющих. Эти показатели объединены в три группы: выходные (группа Y), управляющие (группа X), а также характеристики, отражающие состояние «внешней» среды (группа Z), которые не поддаются оперативному эффективному регулированию на местном уровне. Приведем перечень показателей в каждой из групп.

Эксплуатационные показатели, определяющие качество функционирования дороги в смысле грузовой работы:

y1 – грузооборот (млн т•км);

y2 – производительность локомотива (т•км);

y3 – участковая скорость (км/ч);

y4 – средний вес грузового поезда (т);

y5 – простой местного вагона (ч);

y6 – простой на технической станции (ч);

y7 – погрузка (тыс. т).

Управляющие факторы (то есть поддающиеся регулированию со стороны руководства дорогой):

x1 – прием груженых вагонов;

x2 – прием порожних вагонов;

x3 – динамическая нагрузка (т•км/км);

x4 – передача по стыкам (поездов);

x5 – среднесуточный пробег локомотива (км);

x6 – эксплуатируемый парк локомотивов (шт.);

x7 – техническая скорость (км/ч);

x8 – статическая нагрузка (т/ваг.);

x9 – средний состав поезда (ваг.);

x10 – простой под одной грузовой операцией (ч);

x11 – выгрузка (ваг.);

x12 – рабочий парк вагонов дороги (ваг.);

x13 – оборот грузового вагона (сут.);

x14 – заявленный объем перевозок (тыс. т);

x15 – наличие парка вагонов (тыс. шт.).

Внешние показатели:

z1 – провозная способность железнодорожной линии (млн т•км);

z2 – валовой внутренний продукт страны (трлн руб.).

Мы не будем приводить здесь все соотношения модели – в [6] они подробно описаны. Заметим только, что при построении её регрессионных уравнений активно использовались алгоритмы и программные средства, описанные в работах [2–5], а также находящаяся в свободном доступе в Интернете программа Gretl. Анализ модели с применением принятых в регрессионном анализе критериев адекватности указывает на её высокие аппроксимирующие и прогностические характеристики, что позволяет эффективно использовать эту модель для решения широкого круга проблем, связанных со среднесрочным прогнозированием развития объекта исследований.

Модель содержит семь уравнений для выходных переменных и шесть – для управляющих.

Как отмечается в работе [6], процесс многовариантного прогнозирования будущих значений выходных переменных состоит в задании в рамках специально разработанного сценария соответствующих значений управляющих переменных x6, x8, x9, x10, x11, x12, x13, x15, для которых отсутствуют уравнения, а также значений внешних переменных z1 и z2. Рассмотрим вопрос разработки прогнозного сценария, который был бы эффективен в данном случае.

Разработка прогнозного сценария

Возможный подход к решению проблемы мог бы состоять в следующем. Можно разработать три варианта прогнозов – пессимистичный, оптимистичный и нейтральный. Первый основывается на предположении, что события будут развиваться наихудшим образом, второй – наилучшим, а третий базируется на гипотезе, что те тенденции в развитии процесса, которые имели место на предыстории (2000–2014 гг.), будут продолжены и в будущем. При среднесрочном прогнозировании (на 2015–2019 гг.) в качестве значений входных переменных модели можно было бы принять для первого варианта их минимальные значения на предыстории, второго – максимальные, третьего – усредненные. Так, однако, поступать категорически нельзя, поскольку анализируемый процесс имеет ярко выраженный динамический характер, и то, что хорошо для 2014 г., может оказаться плохо для прогнозного периода.

Поэтому представляется, что более оправданным является следующий подход.

Для каждой входной переменной r строится тренд, например линейный:

(*)

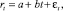
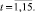Далее для нейтрального прогноза рассчитываются будущие значения r на основе уравнения (*). Для пессимистичного прогноза значение углового коэффициента b уменьшается на 25 % (если r имеет позитивный характер и b > 0), а для оптимистичного – увеличивается на 25 %.

В табл. 1 приведены соответствующие тренды.

Таблица 1

Линейные тренды

Для них не приводятся значения критериев адекватности, поскольку это не является принципиальным – главное, что уравнения, аналогичные (*), в любом случае отражают общую для предыстории тенденцию в динамике соответствующей переменной.

Данный подход был реализован авторами при разработке прогнозного программного комплекса БИВИН [1], который и был использован при среднесрочном прогнозировании значений эксплуатационных показателей функционирования Красноярской железной дороги.

Результаты прогнозирования

В нижерасположенных табл. 2, 3, 4 и на графиках на рисунке приведены прогнозные значения эксплуатационных показателей.

Таблица 2

Пессимистичный прогноз

Таблица 3

Нейтральный прогноз

Таблица 4

Оптимистичный прогноз

Таблица 5

Реальные значения всех переменных за 2015 г.

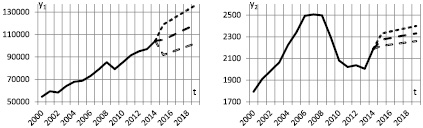
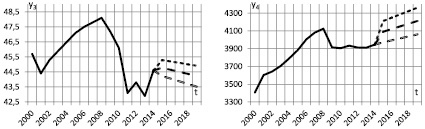
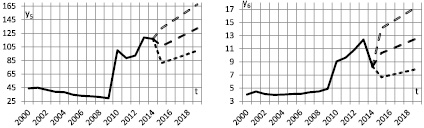
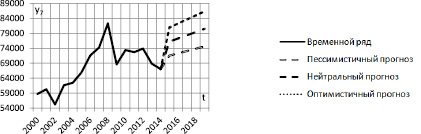
Прогнозные значения эксплуатационных показателей

Естественный интерес вызывает сравнение прогнозных значений выходных переменных на 2015 г. с реальными. В табл. 5 приведены значения всех переменных модели за 2015 г.

Итак, фактические значения всех выходных переменных y1, …, y7 попали в интервалы, границами которых служат пессимистичные и оптимистичные прогнозные значения. Причем значения переменных y2, y4, y7 ближе к пессимистичным прогнозам, переменных y1, y5 – к нейтральным, а переменных y3, y6 – к оптимистичным. Абсолютные ошибки нейтрального прогноза для переменных y1, …, y7 составляют соответственно 4222; –39,8; 50,23; –119,2; 3,69; –2,44; –4048.

Таблица 6

Приросты показателей по отношению к 2014 г. (пессимистичный прогноз)

Таблица 7

Приросты показателей по отношению к 2014 г. (нейтральный прогноз)

Таблица 8

Приросты показателей по отношению к 2014 г. (оптимистичный прогноз)

Особый интерес представляет информация о приросте (в процентах) значений показателей по отношению к 2014 г. для всех трех признаков. Эта информация представлена в табл. 6, 7 и 8.

Выводы

Все полученные результаты являются существенным доводом в пользу справедливости тезиса о высокой адекватности математической модели динамики эксплуатационных показателей функционирования Красноярской железной дороги. Модель может быть эффективно использована для прогнозирования этих показателей на среднесрочную перспективу, поскольку открывает широкую возможность путем варьирования значений входных переменных рассчитывать значения выходных, их анализировать и вырабатывать рациональные управленческие решения по регулированию деятельности дороги.