В настоящее время всё большее развитие и распространение получает имитационное моделирование. Это обусловлено возросшей необходимостью исследования сложных систем, а имитационное моделирование небезосновательно считают одним из наиболее эффективных методов исследования таких систем [3].
При решении задач оптимизации управления в сфере банковской деятельности приходится иметь дело с системами массового обслуживания (СМО), которые предназначены для многократного выполнения однотипных задач. Каждая система массового обслуживания предназначена для выполнения некоторого потока требований (заявок), которые поступают на вход системы в случайные моменты времени. Обслуживание этих заявок в общем случае длится случайное время. Именно случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО.
Любая система массового обслуживания характеризуется показателями ее эффективности. Поэтому при формализации задач обслуживания вполне естественно стремление построить СМО таким образом, чтобы установить разумный компромисс между показателями, связанными с заявками и полнотой использования возможностей системы. При моделировании СМО необходимо выбрать такой показатель ее эффективности, который учитывает одновременно требования и возможности и тех, кого обслуживает, и тех, кто обслуживает. В качестве показателя экономической эффективности может быть выбран минимум затрат, связанных с обращением системы (затраты, связанные с эксплуатацией СМО и простоем каналов обслуживания) и обслуживания заявок (потери, связанные с пребыванием заявок в очереди и с уходом необслуженных заявок) [1]. В исследовании [7] представлена комплексная статистическая имитационная модель СМО торгового предприятия. В качестве показателя ее эффективности выбрано количество каналов обслуживания, при котором число обслуженных заявок обеспечивает максимум функции чистой прибыли, учитывающей налоговые отчисления, размер заработной платы кассиров и стимулирующие надбавки персоналу, величину наценки на товары различных категорий и недополученную прибыль от различных категорий товаров.
Реальные системы массового обслуживания, как правило, состоят из большого числа элементов и имеют сложные внутренние связи. Использование аналитических моделей в таких случаях не позволяет получить достоверных результатов, и зачастую для построения и изучения СМО переходят к имитационным моделям [2]. Целью исследования является построение имитационной модели деятельности отделения банка по обслуживанию физических лиц на основе дискретно-событийного подхода. При этом отделение банка рассматривается как система массового обслуживания с s устройствами, каждое из которых может одновременно обслуживать только одно требование.
Постановка задачи моделирования
Программная модель системы массового обслуживания должна адекватно отражать поведение элементов системы в процессе ее функционирования, т.е. в их взаимодействии друг с другом и внешней средой, и в то же время не создавать трудностей при ее реализации.
В основе разработки программной реализации СМО используется принцип дискретно-событийного моделирования. Дискретно-событийное моделирование используется для построения моделей, отражающих развитие системы во времени, когда состояния переменных системы меняются мгновенно в конкретные моменты времени [6]. Состояние системы определяется как совокупность переменных, необходимых для ее описания на определенный момент времени в соответствии с задачей исследования. Например, при исследовании работы банка переменными состояния могут служить: число занятых кассиров, число посетителей в банке, время прибытия каждого клиента в банк и др. В качестве критерия остановки прогона при имитационном моделировании могут выступать обработка определенного количества требований или достижение определенного времени моделирования. При моделировании СМО также следует учитывать влияние вида закона распределения входного потока заявок на статистические характеристики выходных параметров системы [5]. Поэтому оптимизировать характеристики эффективности системы в целом невозможно без учета влияния вида закона распределения входного потока заявок.
Интервалы времени между поступлением требований являются независимыми случайными величинами со средним значением μA. Время обслуживания также является случайной некоррелированной с интервалами поступления требований величиной. Среднее значение времени обслуживания требований – μS. В качестве входных параметров системы выберем количество каналов обслуживания s, среднее время поступления заявок μA, среднее время обработки требований μS, длину очереди l. В качестве выходных параметров системы будем рассматривать следующие показатели: коэффициент использования системы, среднее время ожидания заявки в очереди, среднее время пребывания заявки в системе, среднее по времени число требований в очереди, среднее по времени число требований в системе, относительная пропускная способность системы. При оценке эффективности работы СМО необходимо сопоставить доходы от выполнения заявок с потерями от простоя каналов обслуживания (с одной стороны, будем иметь высокую пропускную способность, а с другой стороны – значительный простой каналов обслуживания) и выбрать компромиссное решение.
Пример имитационной модели и предложения по оптимизации
Рассмотрим работу отделения банка по обслуживанию физических лиц с дисциплиной обслуживания – FIFO (First-In, First-Out) – очередь: требования обслуживаются по принципу «первым пришел – первым обслужен». Для исследования интенсивности входного потока заявок собрана статистическая информация. В течение каждого дня недели время поступления клиентов изменяется от 9 до 20 часов. Время между приходом двух клиентов является случайной величиной с показательным законом распределения (μA = 5 мин), а время обслуживания подчиняется нормальному закону распределения с математическим ожиданием μS = 6,5 мин и средним квадратическим отклонением 3 мин. В том случае, если в момент прихода нового клиента оператор занят, то клиент встает в очередь. При этом имеются места ожидания, число которых равно 10. Если же все места заняты, то клиент уходит и не ждет обслуживания. Для работы по обслуживанию клиентов привлечены два оператора.
Для проведения имитационного эксперимента деятельности отделения в течение одного рабочего дня выбрана среда моделирования SimEvents пакета MATLAB+Simulink, имеющего большой набор различных блоков, которые обеспечивают различные воздействия с временными и функциональными зависимостями, а также блоки получателей информации [4].
При дискретно-событийном моделировании используется понятие сущностей (entities), которые могут перемещаться через сети очередей (queues), серверов (servers) и переключателей (switches), управляемых дискретными событиями, в процессе моделирования. Графические блоки SimEvents могут представлять компонент, который обрабатывает сущности, но сами сущности не имеют графического представления. Ключевые процессы моделирования состоят из следующих основных блоков: генерации сущностей (блок Time-Based Entity Generator), хранения сущностей в очереди (блок FIFO Queue), обслуживания сущностей (блок SingleServer) и отображения информации о ходе моделирования (блоки SignalScope или Display). Для каждого блока необходимо установить параметры, которые соответствуют требованиям моделируемой системы.
Установим время моделирования 660 мин, что соответствует времени работы отделения с 9 до 20. Схема полученной модели и результаты моделирования представлены на рис. 1.
Блок SignalScope характеризует процедуру прохождения требований через накопитель. Из графика, изображенного на рис. 2, видно, что не все заявки сразу поступают на обслуживание, некоторые заявки формируют очередь.
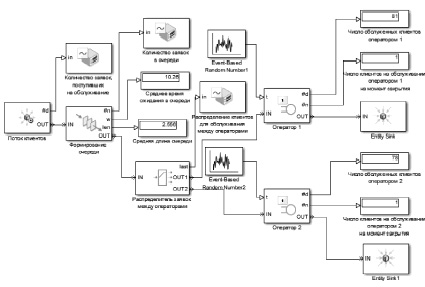
Рис. 1. Схема модели и результаты моделирования работы отделения банка при наличии двух операторов-кассиров
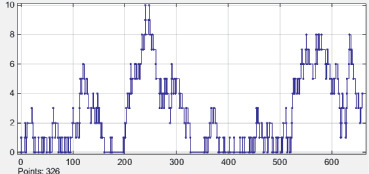
Рис. 2. Процедура прохождения заявок через накопитель
По результатам проведения имитационного моделирования работы отделения банка по обслуживанию физических лиц можно сделать следующие выводы:
– в течение одного рабочего дня в отделение приходят в среднем 165 клиентов, из которых в течение рабочего дня обслуженными оказываются 159 клиентов т.е. относительная пропускная способность составляет 96,4 %;
– среднее время ожидания клиентом обслуживания составляет 10,26 минут;
– среднее число клиентов, находящихся в очереди, составляет 2,6 человека;
– на момент закрытия в очереди остается четыре требования и двое клиентов находятся на обслуживании операторами;
– в течение рабочего дня оба оператора оказываются примерно одинаково загруженными, при этом первый оператор обслуживает 50,9 % поступивших на обслуживание требований. Коэффициент использования системы составляет 78,3 %.
Очевидно, что относительная пропускная способность данной системы достаточно высокая, но время пребывания клиентов в очереди весьма продолжительное. Анализ других характеристик эффективности обслуживания при наличии двух операторов свидетельствует о значительной перегрузке отделения. Поэтому для улучшения работы с клиентами рекомендуется либо сократить среднее время обслуживания клиента, что может повлечь за собой снижение качества обслуживания и увеличение неудовлетворенности этим обслуживанием, либо увеличить число операторов-кассиров, что повлечет за собой дополнительные издержки по содержанию и обслуживанию дополнительного канала обслуживания. Рассмотрим модель работы рассматриваемого отделения при наличии трех операторов и прежних входных данных.
В результате проведенного моделирования работы данного отделения банка получены следующие результаты:
– в течение одного рабочего дня в отделение обратилось 128 клиентов, из которых 123 были обслужены оператором, т.е.относительная пропускная способность системы составляет 96 %;
– среднее время ожидания клиентом обслуживания сократилось до 0,49 минуты;
– среднее число клиентов, находящихся в очереди уменьшилось и составило 0,1 человек;
– на момент закрытия в очереди остается два клиента и трое клиентов находятся на обслуживании операторами;
– в течение рабочего дня наиболее загруженным является первый оператор, который обслуживает 56 клиентов, т.е. 45,53 % поступивших на обслуживание требований, менее загруженным – второй оператор, обслуживающий 42 заявки, т.е. 34,15 % поступивших на обслуживание требований, а на обслуживании третьим оператором остаётся 25 клиентов, что составляет 20,32 %. При этом коэффициент использования системы составляет 40,38 %.
Поведенная оптимизация показала, что при наличии трех операторов-кассиров отказы в работе с клиентами будут отсутствовать, т.е. исчезнет недополученная прибыль. Эксперимент показал, что использовать трех кассиров целесообразно в периоды с 10:30 до 14:00 и с 17:30 до 20:00. Однако экономический эффект от данного мероприятия можно наблюдать в долгосрочной перспективе.
Выводы
Созданная имитационная модель системы массового обслуживания вполне адекватно отражает работу отделения банка и может быть применена для моделирования аналогичных систем массового обслуживания. Применение современных средств визуально-ориентированного программирования позволяет использовать возможности виртуальных средств регистрации и визуализации результатов.
Созданная имитационная модель СМО отделения банка позволяет проводить оптимизацию наиболее значимых параметров системы и может быть составной частью системы поддержки принятия решений для рационализации организационной структуры и оптимизации управления.
Результаты работы модели можно считать корректными при достоверных исходных данных. Проведенный эксперимент показал, что затраты компьютерного времени, которые считаются одним из основных недостатков имитационного моделирования, не являются критичными при реальных параметрах СМО. Полученные результаты подтверждают эффективность методов компьютерного имитационного моделирования для диагностики и оптимизации систем массового обслуживания.



