Для информационной системы важным принципом построения является надежность. Информационная система должна быть максимально защищена от несанкционированного доступа к информации, а также должна полностью отображать информационные и функциональные параметры. Надежность информационной системы обеспечивается с помощью средств адекватных назначению и масштабу системы в процессе хранения и обработки данных. Также следует особо выделить безотказное выполнение функций информационной системой на всех этапах эксплуатации [8].
Комплексный показатель надежности информационной системы обусловлен целым рядом факторов: конструктивных, производственно-технологических, эксплуатационных и др. Многообразие факторов, влияющих на надежность информационной системы, носит случайный характер процессов изменения свойств во времени, приводящий к изменениям характеристик и отказам системы. Поэтому надежность информационных систем описывается вероятностно-статистическими закономерностями [4].
Надежность информационных систем должна решаться на всех стадиях жизненного цикла системы. Надежность является внутренним свойством информационной системы, заложенным при ее создании и проявляющимся во времени при функционировании и эксплуатации.
Таким образом, в процессе функционирования информационная система может находиться в одном из некоторого множества состояний (фаз), причем каждое из состояний характеризуется определенным уровнем надежности, т.е. переход из одного состояния в другое определяется показателями надежности информационной системы, в частности «интенсивностями переходов» – условными плотностями вероятностей переходов [1].
Одним из наиболее распространенных методов исследования состояний информационной системы является метод интенсивностей переходов, основанный на предположении о пуассоновском потоке редких событий, переводящих информационную систему из одного состояния в другое, т.е. поток событий обладает свойствами ординарности и отсутствия последействия [2].
Для пуассоновского потока [7]:
<
1) вероятность появления на интервале времени (0, t) m событий равна
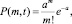(m = 0, 1, 2, ...), (1)
где а – математическое ожидание числа событий на участке от t0 до t0 + t, равное
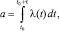
l(t) – интенсивность (плотность) потока событий, причем для простейшего потока l(t) = l = const;
2) интервал времени между событиями распределен по экспоненциальному закону.
При таких предположениях можно составить и решить систему дифференциальных уравнений А.Н. Колмогорова [7], построив ориентированный граф, вершинами которого являются состояния информационной системы, а направленные ребра – интенсивности и направления возможных переходов.
Решение дифференциальных уравнений осуществляется с использованием преобразований Лапласа, позволяющих свести их к алгебраическим уравнениям.
Рассмотрим на примере исследование состояний информационной системы, которая может находиться в двух состояниях: работоспособном (S1) и неработоспособном (S2); l – интенсивность простейшего потока отказов информационной системы, m – интенсивность простейшего потока восстановлений работоспособности информационной системы.
Тогда граф состояний рассматриваемой информационной системы имеет вид, представленный на рис. 1
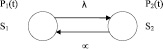
Рис. 1. Граф состояний системы
Дифференциальные уравнения, соответствующие графу состояний на рис. 1, в соответствии с вышеприведенными правилами будут иметь вид
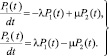(2)
Так как состояния S1 и S2 несовместимы, т.е. составляют полную группу событий, то Р1(t) + P2(t) = 1.
Задавая различные начальные условия (при t = 0), с помощью преобразований Лапласа можно получить значения вероятностей P1(t) и P2(t).
а) Пусть Р1(0) = 1 и Р2(0) = 0, т.е. начальное состояние информационной системы работоспособно. Используя преобразования Лапласа, получим
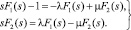(3)
Переходя от изображений к оригиналам, получим
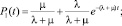(4)
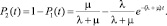(5)
б) Пусть Р1(0) = 0 и Р2(0) = 1, т.е. начальное состояние информационной системы неработоспособно. Тогда аналогично получим
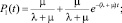(6)
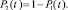(7)
Таким образом, полученные соотношения позволяют определить вероятности двух состояний информационной системы в произвольный момент времени t из различных начальных состояний.
Расчеты по определению вероятностей состояния информационной системы можно автоматизировать (например, для автоматизации использовать математический пакет MathCAD) [6]. Список характеристик информационной системы может быть расширен. Кроме определения вероятностей состояния информационной системы, могут быть вычислены показатели безотказности: вероятность безотказной работы, вероятность отказа, средняя наработка до отказа, средняя наработка на отказ, интенсивность отказов и т.п. [5].
Для увеличения надежности любой информационной системы применяется резервирование. Любое резервирование основывается на включении в состав системы дополнительных средств. В нашем случае – дополнительных механизмов защиты. Использование в системе защиты дополнительных механизмов можно рассматривать не только с целью расширения функций встроенных механизмов защиты, но и с целью их резервирования.
Аналогично тому, как это выполнено в теории надежности информационных систем, определены следующие показатели: вероятность безотказной работы нерезервированной и резервированной системы [3]. Как показали исследования, исходная нерезервированная система недостаточно надежна и не может обеспечить требуемый риск.
Для повышения надежности функционирования информационной системы исследовали два вида резервирования: с постоянно включенным резервом и по методу замещения.
Приведем пример вычисления вероятности безотказной работы нерезервированной и резервированной информационной системы.
Пусть вероятность того, что в любой момент времени (на рассматриваемом промежутке работы равном 1000 часов) объект защищен нерезервированной системой, равна
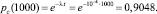
Далее для определения вероятности безотказной Pc(t) работы резервированной информационной системы составим и решим систему дифференциальных уравнений [7]:
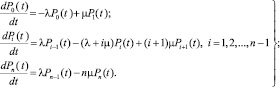(8)
В результате преобразований получены значения вероятности безотказной работы информационной системы с постоянно включенным резервом для значения интенсивности восстановления системы ρ = 0,1 время восстановления системы защиты Tv = 8 недель и ρ = 0,01 при Тv = 1 неделя.
Вероятность того, что в момент времени от 0 до 1000 часов информационная система работает безотказно, для ρ = 0,01 выше, чем при ρ = 0,1. Как показывает графическая зависимость, представленная на рис. 2, с увеличением времени непрерывной работы вероятность безотказной работы уменьшается.
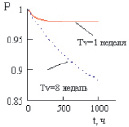
Рис. 2. Вероятность безотказной работы информационной системы с постоянно включенным резервом
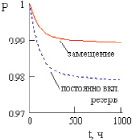
Рис. 3. Вероятность безотказной работы информационной системы с постоянно включенным резервом
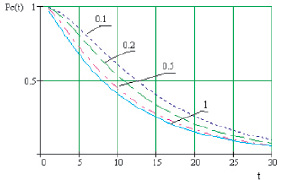
Рис. 4. Зависимость безотказной работы Pc(t) при различных значениях интенсивности λ
Как показывает анализ графических зависимостей представленных на рис. 3, вероятность безотказной работы информационной системы с замещением выше, чем вероятность безотказной работы системы с постоянно включенным резервом.
Анализируя полученные результаты, можно сделать следующие выводы:
– время восстановления (время устранения уязвимостей) должно служить требованием к предприятию разработчику информационной системы;
– с увеличением времени непрерывной работы вероятность того, что информационная система безотказно работает, уменьшается;
– из двух указанных видов резервирования наибольший выигрыш надежности достигается при резервировании замещением.
Однако это резервирование имеет два существенных недостатка:
– для его физической реализуемости требуется автомат контроля состояния системы и коммутации при отказе работающей системы;
– производительность информационной системы уменьшается.
На рис. 4 приведены графики вероятностей безотказной работы информационной системы Pc(t) для случая λ = 0,1; 0,2; 0,5; 1 с использованием автомата контроля и коммутации системы.
Из графиков видно, что автомат контроля и коммутации влияет на вероятность безотказной работы резервированной информационной системы. Причем для случая, когда λ1 = 0,1, вероятность безотказной работы системы наибольшая, а при λ1 = 1 – вероятность безотказной работы наименьшая. Из двух рассмотренных видов резервирования наибольший выигрыш надежности системы защиты достигается при резервировании замещением, если автомат контроля состояния информационной системы и коммутации при отказе работающей системы «идеален» с точки зрения отказоустойчивости.