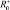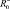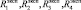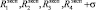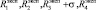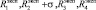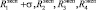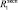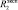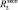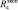В работах [3–5] приведены математические модели, позволяющие имитировать роботами эмоциональное поведение человека. Эмоции человека, имитируемые роботом, назовем псевдоэмоциями, а воспитание робота, полученное в результате псевдоэмоций, назовем псевдовоспитанием. В работе [6] впервые описаны модели комплексных псевдоэмоций робота и комплексных эмоций человека. Частным случаем комплексных псевдоэмоций робота и эмоций человека являются амбивалентные псевдоэмоции и амбивалентные эмоции.
В работе [8] предложена математическая модель амбивалентных псевдоэмоций роботов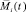 
, которая представляет вектор 
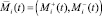, где 
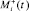и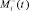 
удовлетворяют условиям 
, 
, 
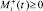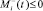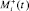и 
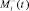удовлетворяют математическому определению псевдоэмоции [5], t – текущее время действия псевдоэмоции, i – порядковый номер псевдовоспитательного такта, i = 1, 2, 3, ... [5].
Введем гипотезу о том, что любая псевдоэмоция робота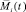 
представима в виде вектора
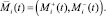
Рассмотрим равномернозабывчивых роботов [5].
Будем считать, что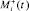 
порождает воспитание 
, 
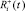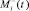порождает воспитание 
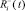, где
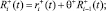
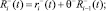
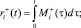
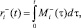
где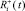 
– псевдовоспитание робота, порожденное неотрицательной компонентой амбивалентной псевдоэмоции 
; 
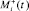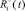– псевдовоспитание робота, порожденное неотрицательной компонентой амбивалентной псевдоэмоции 
, 
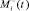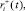
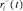– элементарные псевдовоспитания роботов, порожденные псевдоэмоциями 
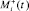и 
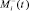соответственно; θ+ и θ– – коэффициенты памяти положительной компоненты и отрицательной компоненты амбивалентной псевдоэмоции, характеризующие запоминание роботом псевдовоспитани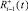й 
и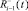 
соответственно, θ+ ∈ [1, 1], θ– ∈ [1, 1].
Введем следующее определение.
Незлопамятным роботом назовем робота, для которого справедливо неравенство θ+ > θ–, робота для коэффициентов памяти которого выполняется θ+ < θ-, назовем злопамятным.
Способ разложения псевдоэмоции на вектор амбивалентных псевдоэмоций
Предположим, что робот испытал единственную псевдоэмоцию M0, породившую псевдовоспитание R0, которое соответствует паре псевдовоспитаний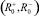 
, причем справедливо соотношение
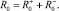
Пусть при фиктивном такте [5] с порядковым номером i робот имеет псевдовоспитание Ri, причем справедливы формулы
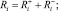
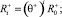
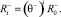
Пусть выполнено n фиктивных тактов [5]. Пусть для каждого из фиктивных тактов на основе экспериментов измерено значение псевдовоспитания робота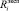 
в конце фиктивного такта с номером i. Отметим, что в работе [7] описан один из способов измерения псевдовоспитаний и псевдоэмоций, поэтому допущение о возможности измерения 
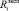не является критичным.
Для фиктивного такта с номером i значение отклонения экспериментального псевдовоспитания от расчетного псевдовоспитания зададим формулой
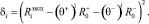
Очевидно, что для фиктивных тактов, количество которых равно n, суммарное значение отклонения экспериментального псевдовоспитания от расчетного псевдовоспитания Δ удовлетворяет соотношению
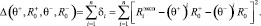(1)
Очевидно, что для того, чтобы величины θ+ , θ– ,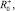 
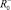адекватно описывали псевдовоспитательный процесс при фиктивных тактах, величина Δ должна быть минимальна с учетом следующих ограничений:
θ+ ∈ [0, 1]; θ– ∈ [0, 1];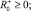 
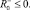(2)
Используем метод Лагранжа [6] для определения условного экстремума функции (1) с ограничениями (2).
Стоит отметить, что для однозначного определения значений 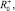θ+, 
θ–,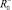 
необходимо выполнение неравенства n ≥ 4.
Для решения поставленной задачи разработана программа в пакете Mathematica [2]. Входными параметрами для программы является набор чисел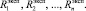 
На выходе программа возвращает значения, для которых значение целевой функции Δ минимально.
Приведем примеры определения значений 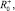θ+, 
θ–,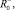 
полученные на основе разработанной программы по заданным экспериментальным значениям.
Пример 1
Для следующих значений псевдовоспитаний: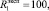 
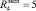получены соответствующие значения 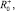θ+, 
θ–,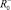 
: 
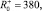
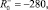θ+ = 0,24, θ– = 0,07.
Таким образом, согласно введенному выше определению можно сделать вывод о том, что рассмотренный робот является незлопамятным.
Пример 2
Для численных значений входных параметров псевдовоспитаний робота
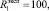
получены следующие значения 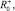θ+, 
θ-,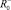 
:
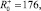
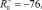θ+ = 0,46, θ- = 0,72.
Таким образом, можно сделать вывод о том, что этот робот является злопамятным.
Легко видеть, что, задавая коэффициенты θ+, θ-, можно проектировать злопамятных или незлопамятных роботов. В этом случае для определения величин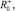 
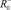необходимо минимизировать целевую функцию (1) с заданными коэффициентами θ+, θ- при выполнении условия (2). Таким образом, количество необходимых экспериментальных значений для определения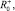 
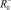уменьшается до двух.
Исследование математической модели
При изучении математической модели на устойчивость каждый из входных параметров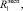 
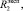
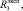
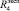увеличивался на величину σ, равную 1 % от эталонного значения. Эталонное значение соответствует данным второй строки табл. 1.
Анализ табл. 1 позволяет утверждать, что изменение исходных параметров на 1 % влечет изменение параметров, возвращаемых моделью, не более чем на 18 %. Таким образом, математическая модель устойчива относительно входных параметров.
Предлагая метод определения злопамятности или незлопамятности робота, целью которого является построение робота – психологического аналога человека, важно верифицировать математическую модель натурными экспериментами, проведенными с людьми.
В работе [9] описана компьютерная программа, позволяющая численно измерять эмоциональное состояние человека на основе микровибраций его головы. В работе [7] описаны экспериментальные значения воспитаний человека для фиктивных тактов. Эти значения помещены в табл. 2. На основе решения задачи минимизации функции (1) при ограничениях (2) вычислены значения коэффициентов θ+, θ- для испытуемых, которые также приведены в табл. 2. Соответствие рассчитанных коэффициентов памяти результатам экспертного оценивания, проведенного с помощью известных психологических методов определения злопамятности или незлопамятности человека, приведены в последней колонке табл. 2.
Анализ табл. 2 позволяет утверждать, что предложенная методика определения злопамятных или незлопамятных людей позволяет получать верные результаты в 87 % случаев.
Таблица 1
Характеристики устойчивости модели
|
|
|
θ+ |
θ- |
|
|
|
380 |
–280 |
0,24 |
0,07 |
|
|
366 |
–266 |
0,24 |
0,07 |
|
|
431 |
–331 |
0,23 |
0,08 |
|
|
365 |
–265 |
0,24 |
0,06 |
|
|
380 |
–280 |
0,24 |
0,07 |
Таблица 2
Результаты верификации модели натурными экспериментами
|
№ п/п |
|
|
|
|
θ+ |
θ- |
Экспертная оценка |
|
1 |
227 |
202 |
174 |
148 |
0,84 |
0,34 |
Незлопамятные |
|
2 |
148 |
145 |
142 |
139 |
0,97 |
0,92 |
Незлопамятные |
|
3 |
151 |
140 |
126 |
112 |
0,88 |
0,39 |
Незлопамятные |
|
4 |
162 |
160 |
154 |
148 |
0,96 |
0,06 |
Незлопамятные |
|
5 |
211 |
181 |
150 |
122 |
0,79 |
0,48 |
Незлопамятные |
|
6 |
157 |
151 |
145 |
134 |
0,8 |
0,83 |
Злопамятные |
|
7 |
227 |
209 |
193 |
171 |
0,81 |
0,78 |
Незлопамятные |
|
8 |
193 |
183 |
176 |
165 |
0,89 |
0,89 |
Злопамятные |
Заключение
Таким образом, в настоящей публикации впервые предложена математическая модель злопамятных и незлопамятных роботов, основанная на амбивалентных псевдоэмоциях. Эта модель позволяет проектировать роботов с заданными психологическими характеристиками (злопамятностью и незлопамятностью). На основе проведенных численных и натурных экспериментов можно сделать вывод о том, что способ определения злопамятных или незлопамятных роботов адекватно отражает реальные психологические качества человека.
Предложенная модель злопамятных и незлопамятных роботов может быть использована при разработке нового класса компьютерных игр, учитывающих психологическое поведение их героев. Одним из возможных применений предложенного в статье метода определения злопамятных или незлопамятных людей может быть, например, определение психологических качеств человека при приеме на работу, формирование групп людей, члены которых будут наиболее дружественно настроены друг к другу, что, на наш взгляд, будет определять отсутствие конфликтов в группе при выполнении заданий, и т.д.