В работе рассматривается применение искусственной поперечной циркуляции для защиты нижних бьефов гидроузлов от размыва [4]. Наиболее эффективным среди известных способов регулирования русловых процессов, основанных на создании искусственной поперечной циркуляции, является использование донных галерей М.В. Потапова [5]. Расчеты действия поперечных донных галерей в MathCAD по методу источников для условий водосливной плотины Чебоксарской ГЭС показали их недостаточную эффективность [3]. С учетом того, что галерея не может быть установлена непосредственно в месте размыва, ее применение малоэффективно. Установка галерей на действующем гидроузле является сложной технической задачей. Это вызывает необходимость разработки регуляторов скорости потока, основанных на новом принципе действия.
При использовании в качестве средств регулирования кинематических характеристик водного потока распределенных завихрений могут быть получены новые технические решения (рис. 1), позволяющие реализовать гашение придонных скоростей до уровня, обеспечивающего устойчивость дна нижнего бьефа.
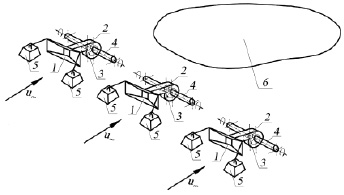
Рис. 1. Расположение системы вихревых камер в потоке: 1 – конфузор; 2 – подводящий патрубок; 3 – камера; 4 – направляющий патрубок; 5 – донный якорь; 6 – область размыва
Конструкция устройства для защиты нижних бьефов гидроузлов от размыва на основе систем гидравлически коротких трубопроводов состоит из ряда вихревых камер (рис. 1), расположенных поперек руслового потока подобно поперечной вихревой галерее. Жидкость поступает в каждую из камер через конфузоры 1, в которых ее скорость возрастает, а затем посредством поворотного патрубка 2 направляется в вихревую камеру 3. Из вихревой камеры 3 циркуляционный поток через патрубок 4 направляется наружу. При соединении завихренных потоков смежных камер образуется вихревая структура достаточной длины, имеющая направление вращения, замедляющее скорость в придонном слое.
В качестве математической модели предлагаемых регуляторов может использоваться теория вращательного движения идеальной жидкости [1]. Для описания поступательно-вращательного движения потока использованы уравнения динамики идеальной жидкости в форме Громеки – Ламба в пренебрежении внешними объемными силами.
В цилиндрической системе координат r, θ, z вихрь постоянного радиуса имеет угловую скорость [2]
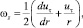(1)
где uτ – касательная скорость в плоскости вихря; r – радиальная координата частицы вихря.
В области за пределами вихря вращение частиц отсутствует, поэтому ωz = 0, и
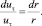(2)
При постоянной интегрирования, выраженной через циркуляцию скорости Γ, интегрирование равенства (2) дает
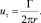(3)
При совпадении вращения вихря с осью z и давлении в бесконечности p∞ уравнение Бернулли имеет вид
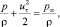(4)
где p – текущее давление; ρ – плотность жидкости.
Избыточное давление при касательных скоростях в поле вихря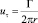 
равно
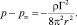(5)
Приращение давления при циркуляции скорости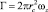 
и радиусе камеры rc равно
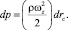(6)
Интегрируя (6) при p = const, ωz = const, и постоянной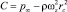 
, найдем
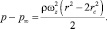(7)
Площадь сечения вихря, через которое жидкость движется поступательно, равна
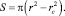(8)
Коэффициент использования сечения вихря равен
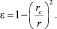(9)
Интеграл Громеки для несжимаемой идеальной жидкости имеет вид
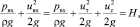(10)
где uвх, uτ, uz – полная, тангенциальная и осевая скорости,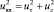 
; H – напор, м.
Проектируя силы на направление радиуса, имеем
dP – dF = 0, (11)
где dP – элементарная сила давления на стенки; dF – элементарная центробежная сила.
Величина элементарной внутренней силы давления на стенки камеры равна
dP = dpSбок = dp2πrl, (12)
где dp – элементарное внутреннее давление; Sбок – площадь боковой поверхности, Sбок = 2Πrl; r, l – внутренний радиус и длина участка камеры.
Элементарная центробежная сила равна
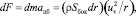(13)
где dm – масса слоя жидкости, dm = ρSбокdr; aцб – центробежное ускорение,
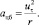(14)
Из условия dF = dP получаем равенство
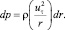(15)
Из сохранения момента количества движения найдем
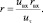(16)
Дифференцируем последнюю формулу
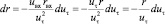(17)
и, подставляя в уравнение (14), получим
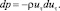(18)
Интегрируем полученное выражение, найдем
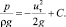(19)
Из условия на границе ядра вихря uτ = uτm следует
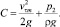(20)
Поэтому
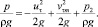(21)
Сопоставляя уравнения (10) и (21), получим
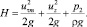(22)
Уравнение неразрывности потока имеет вид
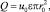
с другой стороны,
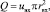
где uвх, rвх, u0, r0 – скорость и радиус входного и выходного сечений камеры.
Сравнивая эти два выражения, получим
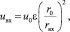(23)
или, с учетом сохранения момента количества движения для неразрывной струи uвхRвх = uτr,
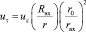и 
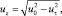(24)
где Rвх – плечо частицы потока, равное расстоянию от оси вращения потока до центра тяжести камеры, Rвх = Rк – rвх; Rк – радиус камеры.
Из (24) тангенциальная скорость около стенки насадка r = r0 равна
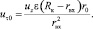(25)
Та же скорость на границе вихря, где нет избыточного давления и r = rm,
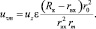(26)
Отсюда, принимая во внимание выражение (9), получаем
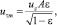(27)
где A – геометрическая характеристика вихревой камеры
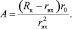(28)
Подставляя значение из выражений (21) и (27) и решая полученное уравнение относительно Δp, находим
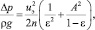(29)
где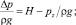 
uэ = uzε.
Отсюда
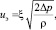(30)
где ξ – коэффициент скорости.
Далее рассматривается расчет в среде MathCAD кинематических характеристик потока, формируемого конструкцией, выполненной в виде вихревой камеры [2].
Численное моделирование в среде MathCAD
Циркуляция скорости Γ := 2 м2/c.
Радиус входного патрубка вихревой камеры r0 := 0,25 м.
Линейная скорость на границе входного патрубка вихревой камеры
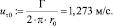
Текущий полярный радиус-вектор r := 0...r0 м.
Текущий угол поворота полярного радиуса-вектора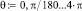 
м.
Компоненты декартовой системы координат x(θ, r) := r•cos (θ), м; y(θ, r) := r•sin (θ), м.
Проекции скорости точки вихря на оси декартовой системы координат (рис. 2):
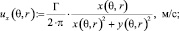
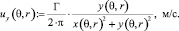
Угловая скорость на границе входного патрубка
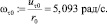
Текущая температура воздуха t := 14 °С.
Текущая температура воздуха
T := t + 273,5 = 287,5 К.
Регрессионная зависимость плотности воды от температуры
ρ(t) := (1000 – 0,062•t – 0,00355•t2) = = 999,082 кг/м3.
Ускорение свободного падения g := 9,81 м/с2.
Удельный расход плотины q := 4,66 м2/с.
Скорость течения в нижнем бьефе vн := 0,83 м/с.
Глубина потока в нижнем бьефе
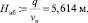
Глубина погружения рассматриваемой точки потока h := 0...Hнб, м.
Гидростатическое давление
p0(h) := ρ(T)•g•h, Па
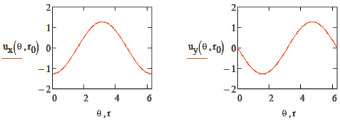
а б
Рис. 2. Компоненты линейной скорости вихря в проекции на оси координат x, y, м
Избыточное давление в центре вихря
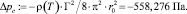
Текущий полярный радиус-вектор r := 0,001...r0, м.
Распределение давления в ядре вихря во входном патрубке вихревой камеры (рис. 3, а)
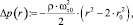Па.
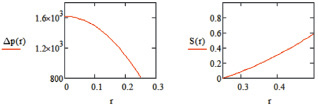
а б
Рис. 3. Изменение давления в ядре вихря (а) и живого сечения (б) от радиуса
Входной радиус вихревой камеры rвх := 0,5 м.
Текущий радиус вихревой камеры r := r0, r0 + 0,01...rвх, м.
Площадь сечения, через которую жидкость движется поступательно (рис. 3, б)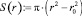 
, м2.
Коэффициент использования сечения вихря (рис. 4, а)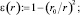 
εi := ε(r).
Осевая скорость на выходе из патрубка u0 := 10,0 м/с.
Коэффициент использования сечения вихря при входе в вихревую камеру
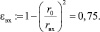
Осевая скорость на входе в вихревую камеру
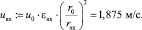
Плечо частицы потока от оси вращения до центра тяжести камеры Rвх := rвх – r0, м.
Тангенциальная скорость в вихревой камере
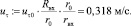
Осевая скорость в вихревой камере
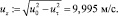
Геометрическая характеристика вихревой камеры
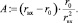
Коэффициент скорости (рис. 4, а)
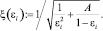
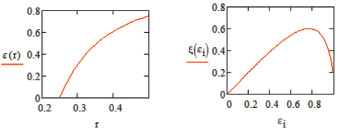
а б
Рис. 4. Зависимость коэффициента использования сечения камеры от ее радиуса (а) и коэффициента скорости от коэффициента использования сечения (б)
Из графика (рис. 4, б) следует, что в зависимости от коэффициента использования сечения вихревой камеры может установиться тот или иной расход. При очень больших или очень малых коэффициентах использования сечения вихревой камеры коэффициент расхода принимает малые значения. В первом случае расход уменьшается за счет малых живых сечений для прохода жидкости, во втором случае – малые значения продольной скорости, снижающиеся за счет с создания больших тангенциальных скоростей в точках, расположенных близко к оси камеры, приводят к уменьшению осевого расхода.
Интерпретация результатов
В результате расчета кинематических характеристик потока в вихревой камере установлено, что в зависимости от коэффициента использования сечения расход через камеру может принимать экстремальное значение. При очень больших или очень малых коэффициентах использования сечения вихревой камеры коэффициент расхода принимает малые значения вплоть до «запирания» системы. В первом случае расход уменьшается за счет малых сечений для прохода жидкости, во втором случае – малые значения продольные скорости, снижающиеся за счет создания больших тангенциальных скоростей в точках, расположенных близко к оси камеры, приводят к уменьшению осевого расхода.
Разработанная информационно-технологическая модель, реализованная в среде MathCAD, позволяет автоматизировать процесс расчета кинематических параметров устройства для гидродинамической защиты нижних бьефов гидроузлов от русловых деформаций на основе систем гидравлически коротких трубопроводов.