Добыча нефти и газа является приоритетным направлением в РФ, поэтому проблема автоматизации и ускорения этого процесса актуальна [3]. Процесс добычи состоит не только из технологической части (бурение скважины и непосредственно добыча), но и научно-исследовательской, а именно изучения данных геофизического исследования скважин, прогнозирования нефтеносных структур, принятия решений на основе изученных данных.
Изначально перспективный нефтегазоносный район исследовали визуально, научившись выявлять присутствие нефтяных залежей по многим косвенным признакам. Однако чтобы поиски были максимально успешными, необходимо уметь «видеть под землей». Это стало возможным благодаря геофизическим методам исследования. Наиболее эффективным инструментом оказался сейсмограф, предназначенный для регистрации землетрясений. Его способность улавливать механические колебания пригодилась и в геологоразведочном деле. Колебания от взрывов динамитных снарядов преломляются подземными структурами, и, регистрируя их, можно определить расположение и форму подземных пластов [4]. По мере развития технологий в арсенал геологов добавлялись новые методы. Например, аэрофотосъемка и космическая съемка обеспечивает более широкий обзор поверхности. Анализ ископаемых остатков с различных глубин помогает точнее определить тип и возраст осадочных пород [4].
Основная тенденция современной геологоразведки – минимальное воздействие на окружающую среду. Как можно большую роль стараются отводить теоретическим предсказаниям и пассивному моделированию. По косвенным признакам можно проследить весь жизненный цикл нефти – где она зарождалась, как двигалась, где находится в настоящее время [4].
Определившись с географическим расположением месторождения нефти и газа, без подробного изучения невозможно установить точную область распространения нефтегазоносного пласта. В такой ситуации целесообразно проводить предпроектные научные исследования, заключающиеся, в частности, в корректном расчете коэффициентов насыщения у совокупности скважин и использовании рассчитанных значений для 3D моделирования нефтегазоносного участка. При этом применяются такие методы исследования скважин, как ядерно-магнитный каротаж (ЯМК) и боковой каротаж (БК) [5]. По рассчитанным данным ЯМК и БК определяются значения коэффициентов насыщения нескольких скважин, находящихся на относительно небольшом расстоянии друг от друга, по которым можно наиболее точно спрогнозировать область распространения нефтегазоносного пласта. На основе рассчитанных данных создается предположительная карта местности с расположенными на ней скважинами, нефтяными и газовыми залежами, находящимися в пределах этих скважин. Подобный механизм позволяет значительно упростить анализ исследуемой области, ускорить процесс прогнозирования и помочь выбрать местоположение и глубину следующей скважины.
Данные для расчета коэффициентов насыщения получают при непосредственном контакте приборов со скважиной. Изначально в скважину помещают исследовательские приборы (зонд, датчики и т.д.) и с их постепенным углублением и получением данных на фиксируемых глубинах методами ядерно-магнитного и бокового каротажа. После проведения всех замеров данные сохраняются в файлах и отправляются специалистам для дальнейшего изучения.
Для расчетов коэффициентов насыщения используются данные в текстовом формате csv, представленные на рис. 1 и 2.
Данные стратиграфии – это список кровель и подошв по каждому из горизонтов скважины (в данном случае для Сибирского региона) в следующем формате:
Горизонт – участок земной коры.
Всего горизонтов 6:
1. Осинский I.
2. Осинский II.
3. Усть-Кутский I.
4. Усть-Кутский II.
5. Преображенский.
6. Ербогученский.
Кровля – начало горизонта.
Подошва – конец горизонта.
wellName – имя скважины.
datasetName – название элемента.
DEPT – глубина.
BP0-BPB – значение бина (результат замера ЯМК) на глубине DEPT.
BK – значение бокового каротажа.
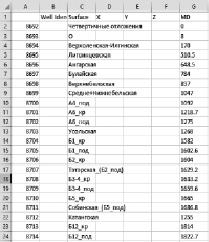
Рис. 1. Данные стратиграфии. Входные данные кровли, подошвы горизонтов
Имея в наличии указанные выше данные, можно провести расчет коэффициентов насыщения. Используемые в расчете алгоритмы интерпретации являются алгоритмами, разработанными ООО РН «Красноярск НИПИ нефть». Корректное определение коэффициента нефтегазонасыщенности (далее Кнг) является одной из основных петрофизических задач. В данном случае для определения Кнг используется уравнение Дахнова – Арчи. Уравнение Дахнова – Арчи, полученное с использованием связей типа «керн-керн», дает повсеместное высокое значение Кнг.
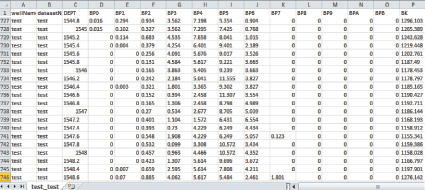
Рис. 2. Входные данные ЯМК и БК
Помимо Кнг производится расчет и других инкрементов насыщения. Список коэффициентов представлен ниже:
- Kn (Кп) – Коэффициент пористости.
- Kn_din (Кпдин) – Динамический коэффициент пористости.
- Kvo (Кво) – Коэффициент остаточной водонасыщенности.
- Pn_Kvo (Рнкво) – Параметр насыщения при коэффициенте остаточной водонасыщенности.
- Pn (Рн) – Текущий параметр насыщения.
- Kv (Кв) – Коэффициент водонасыщенности.
- Kv_p (Кв_подв) – Подвижный коэффициент водонасыщенности.
- Kng (Кнг) – Коэффициент нефтегазонасыщенности.
- Kng_p (Кнг_подв) – Подвижный коэффициент нефтегазонасыщенности.
- Kno (Кно) – Остаточной коэффициент нефтенасыщенности.
- T2_mean (T2_mean) – Среднее логарифмическое время.
- Rвп – Сопротивление водонасыщенного пласта.
- Pp (Рп) – Параметр пористости.
Расчет производится последовательно на основании формул, представленных в докладе Д.В. Назарова, представленного на VI региональной научно-технической конференции «РН-Красноярск НИПИ нефть». Краткое описание расчетов представлено ниже:
1. Kn – Сумма бинов (рис. 2).
2. Kn_din – Сумма двух последних бинов (рис. 2).
3. В качестве характеристики спектра сигнала ЯМК в определенном диапазоне времен T2 рассмотрено среднелогарифмическое время поперечной релаксации T2mean, определяемое формулой
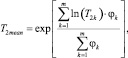 (1)
(1)
где T2k – время k-го бина, начиная с бина, время которого превосходит 3 мс (стандартная отсечка для воды, связанной в глинах); φk – инкрементная пористость k-го бина; m – число бинов, определяющих диапазон рассматриваемых времен релаксации T2.
4. 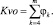 (2)
(2)
Если Kvo = 0 Тогда Kvo = 100.
5. PnKvo = 1394,7•Kvo –1,447. (3)
6. Значение параметра пористости напрямую зависит от горизонта, по которому ведется расчет. Сопоставление формул расчета параметра пористости горизонтам представлено ниже (таблица).
Сопоставление формул расчета параметра пористости горизонтам
|
Горизонт |
Связь Pp – Kn |
|
Осинский I |
Pp = 2563,4*Kn^(–1.379) |
|
Осинский II |
Pp = 2563,4*Kn^(–1.379) |
|
Усть-Кутский I |
Pp = 2136,1*Kn^(–1.24) |
|
Усть-Кутский II |
Pp = 2136.1*Kn^(–1.24) |
|
Преображенский |
Pp = 1620*Kn^(–1.182) |
|
Ербогаченский |
Pp = 3859.5*Kn^(–1.458) |
1. Rвп = Pp•Rв, (4)
где Rв – сопротивление воды, Омм.
2. 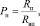
где Rп – сопротивление пласта, Омм; Rвп – сопротивление водонасыщенного пласта, Омм.
Из (4) следует, что
Rвп = Pp•Rв,
Таким образом, уравнение для Pп примет вид
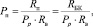 (5)
(5)
где RБК – cопротивление бокового каротажа.
3. 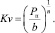 (6)
(6)
4. Рассчитав долю всей воды и значение капиллярно связанной воды, определяется доля подвижной воды:
Kvp = Kv – Kvo. (7)
5. Коэффициента нефтегазонасыщенности рассчитывается следующим образом:
Kng = 1 – Kv. (8)
6. Kngp = Kndin – Kvp, (9)
где Kngp – подвижный коэффициент нефтегазонасыщенности.
7. Остаточный коэффициент нефтенасыщенности является разностью между коэффициентом нефтегазонасыщенности и подвижным коэффициентом нефтегазонасыщенности:
Kno = Kng – Kngp. (10)
После расчета всех коэффициентов насыщения, появляется возможность построения 3D-модели нефтегазоносного пласта, для построения которой было решено провести кубическую интерполяцию на неравномерной сетке [2]. Для построения модели был выбран программный комплекс Matlab. Для интерполяции на неравномерной сетке в этом комплексе выбрана функция griddata.
ZI = griddata(x, y, z, XI, YI) – преобразует поверхность вида z = f(x, у), которая определяется векторами (x, y, z) с обычно неравномерно распределенными элементами. Функция griddata аппроксимирует эту поверхность в точках, определенных векторами (XI, YI) в виде значений ZI. Поверхность всегда проходит через заданные точки. XI и YI обычно формируют однородную сетку (созданную с помощью функции meshgrid) [2].
XI может быть вектором-строкой, в этом случае он определяет матрицу с постоянными столбцами. Точно так же YI может быть вектором-столбцом, тогда он определяет матрицу с постоянными строками [2].
[XI, YI, ZI] = griddata(x, y, z, xi, yi) – возвращает аппроксимирующую матрицу ZI, как описано выше, а также возвращает матрицы XI и YI, сформированные из вектора-столбца xi и вектора-строки yi, аналогичны матрицам, возвращаемым функцией meshgrid:
[...] = griddata (....method) – использует определенный метод интерполяции:
- «nearest» – ступенчатая интерполяция;
- «linear» – линейная интерполяция (принята по умолчанию);
- «cubic» – кубическая интерполяция (используемая для моделирования);
- «v4» – метод, используемый в МATLAB 4.
Метод определяет тип аппроксимирующей поверхности. Метод ‘cubic’ формирует гладкие поверхности, в то время как «linear» и «nearest» имеют разрывы первых и нулевых производных соответственно. Все методы, за исключением v4, основаны на триангуляции Делоне. Метод «v4» включен для обеспечения совместимости с версией 4 системы Matlab [1].
Метод «Интерполяция на неравномерной сетке» строит поверхность на основании указанных точек, соответственно, чем больше точек будет указано, тем точнее будет построена поверхность, т.е. чем больше данных по скважинам будет внесено, тем точнее будет 3D-модель нефтегазоносного пласта. Сами же точки для построения нефтегазоносного пласта определяются из рассчитанных значений коэффициентов насыщения, по каждой скважине может быть выявлено две точки (либо ни одной), определяющие область распространения нефти и газа вдоль скважины.
Помимо данных стратиграфии и данных ЯМК и БК используется дополнительная информация для построения модели, а именно: долгота, широта и высота над уровнем моря по каждой скважине. Эти данные позволяют наиболее точно моделировать расположение скважин друг относительно друга и, как следствие, сам нефтегазоносный участок. Пример модели нефтяного месторождения представлен на рис. 4.
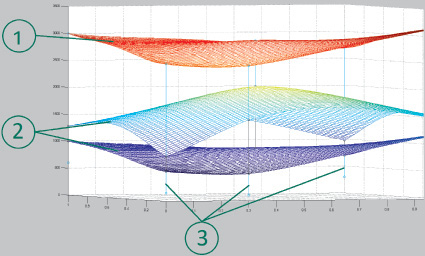
Рис. 4. 3D-модель нефтегазоносного пласта: 1 – схематичное изображение земной поверхности; 2 – верхняя и нижняя поверхности нефтегазоносного пласта; 3 – визуальное отображение скважин
Представленный расчет и визуализация данных позволяет значительно упростить анализ исследуемого нефтяного месторождения, ускорить процесс прогнозирования и помочь в выборе дальнейших действий, таких как определение местоположения и глубины бурения следующей скважины. Разработанный программный модуль Matlab сохраняет все введенные данные в специальном файле проекта, что позволяет быстро вернуться к ранее созданному расчету. В дальнейшем планируется добавить в программный модуль данные, полученные с помощью других измерений, а также возможность отображать спутниковые снимки земной поверхности для повышения информативности 3D модели.



