Несмотря на то, что существует множество приемов и инструментов обнаружения и устранения неполадок в локальной вычислительной сети (ЛВС), администратору необходимо осуществлять сбор данных о работе сети, проводить контроль, анализ и идентификацию всех основных сетевых процессов, т.е. выявлять сетевые проблемы. Такие нестандартные ситуации занимают много рабочего времени IT-специалистов. Для сокращения временных затрат и оптимизации работы администраторов необходимо применить современные технологии в комплексе с интеллектуальной системой поддержки принятия решений (СППР) для идентификации состояния ЛВС [1].
Аналитическая модель сигнатурного анализатора сетевого трафика
Анализ сигнатур – один из первых методов, который использовался для обнаружения проблем в работе компьютерных сетей (КС), связанных с деятельностью злоумышленников. Он базируется на простом понятии совпадения последовательности с эталонным образцом. Во входящем пакете просматривается байт за байтом и сравнивается с сигнатурой – характерной строкой программы, указывающей на наличие вредного трафика.
В качестве сетевой ошибки будем просматривать любую совокупность битовых критериев, которая не генерируется для решения какой-либо полезной задачи в ЛВС.
Структурная схема анализатора трафика представлена на рис. 1.
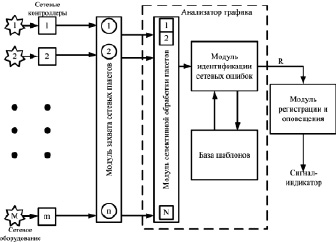
Рис. 1. Структурная схема сигнатурного анализатора сетевого трафика
Процедура анализа включает два этапа:
- селективный сбор фрагментов пакетов;
- распознавание ошибок по образцам.
Обозначим сетевой трафик как поток пакетов в виде множества
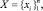
где n – общее число пакетов. Основу образцов представим в виде множества A, объединяющего группы типов ошибок
Aj,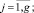 
где g – число групп; Aj – j-й кластер, являющийся множеством однотипных ошибок,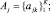 
K – общее число ошибок в j-м кластере.
Ошибка считается найденной, если выполняется условие: X ⊆ A. На вход модуля регистрации подается сигнал R, который может принимать два значения («0» – есть совпадение, «1» – нет совпадения).
Аналитическая модель статистического анализатора сетевого трафика
Статистические методы идентификации сетевых проблем (СП) основаны на том обстоятельстве, что в течение определенного интервала времени (на протяжении суток, часов, минут) могут изменяться некоторые статистические характеристики потока пакетов. В этом случае методы обнаружения нарушений базируются на сравнении текущих характеристик потока пакетов с усредненными характеристиками за некоторый промежуток времени. Первые характеристики называются локальными, а вторые – глобальными.
Если локальные характеристики значительно отличаются от глобальных, то вполне возможна попытка злонамеренных действий, сбоев в работе аппаратуры, программного обеспечения по различным причинам.
Обобщенная схема статистического анализатора, реализующего данный метод идентификации, представлена на рис. 2.
Представим аналитическую модель статистического анализатора, основанного на выборе весовых функций для определения текущих статистических характеристик потока пакетов.
Предположим, что числовая величина Ai (amin ≤ Ai ≤ amax) представляет собой некоторое событие из потока событий, произошедшее в момент времени tj,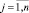 
. Множество событий характеризуется средним значением 
и дисперсией σa величины A.
В качестве статистической характеристики потока событий будем употреблять среднее арифметическое функции f(X) от величины X
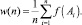(1)
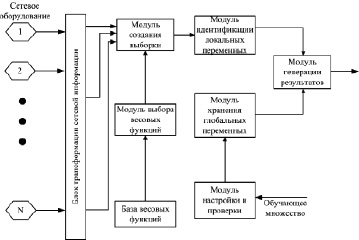
Рис. 2. Обобщенная схема статистического анализатора сетевого трафика
Для определения текущих характеристик будем определять не для всего потока N событий, а только для последних n событий. С этой целью введем понятие весовой функции F(z) и значение текущих характеристик W(N) определим как
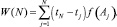(2)
Значение довода характеристики W(N) означает, что ее значение определяется вблизи N-гo события потока, а размер выборки, для которой находится эта величина, определяется видом весовой функции F(z).
Статистические характеристики потока пакетов ЛВС задаются видом функции f(X) в выражении (2). Если функция имеет вид f(X) = X, то значение текущих характеристик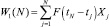 
соответствует среднему арифметическому величины X для последних пакетов сетевого трафика.
Если F(X) = Xk, то
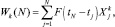
а это есть первый выборочный момент порядка k и т.д.
В случае применения критерия согласия λ2 необходимо разбить величину на D интервалов
[xmin, xmax) = [x0, x1) [x1, x2)...[xD–1, xD),
где x0 = xmin, xD = xmax, и подсчитать число попаданий величины X в тот или иной интервал [2].
Для учета числа событий, попадающих в интервал с номером D, определим функцию
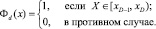
Введем набор величин yd (1 ≤ d ≤ D),
где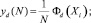 
(3)
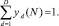(4)
Общее число событий N определяется интервалом времени, в течение которого ведется наблюдение за трафиком. При увеличении числа событий N частоты yd(N) стремятся к Pd – возможностям попадания события в интервал с заданным номером и могут быть применены как глобальные (долговременные) характеристики потока пакетов сетевого трафика.
Для определения текущих (локальных) характеристик будем учитывать число попаданий событий в соответствующие интервалы [xmin, xmax) не для целого потока пакетов, а только для n последних событий. Тогда значение локальных частот Yd можно получить из выражения (2):
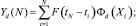(5)
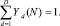(6)
Аналитическая модель нейросетевого анализатора сетевого трафика
Искусственные нейронные сети (ИНС) позволяют более эффективно по сравнению с классическими подходами решать задачи в области обработки и распознавания различных образов [3]. Самая главная задача в применении ИНС для анализа сетевого трафика – это обучить ИНС правильно определять все проблемные события.
ИНС Хемминга предназначена для распознавания класса принадлежности объекта, заданного вектором X биполярных признаков (возможные значения признаков +1 и –1) размерности N. Предполагается, что имеются M классов, каждый из которых характеризуется своим эталонным представителем – объектом Xv, v = 1, 2, ..., V [4, 5].
Эталонные образы и соответствующие векторы признаков хранятся в основе данных. Они отобраны экспертами для разных типов образов. На рис. 3 представлена схема обработки данных при применении нейросетевого классификатора Хемминга.
ИНС Хемминга принимает на N входов биполярные признаки объекта и после обработки данных активизирует один из K выходов, который указывает на класс принадлежности предъявленного на входе объекта.
Критерием отнесения объекта X к классу является квадрат расстояния между векторами X и Xq, q = 1, 2, ..., Q:
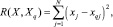(7)
где xj и xqj – j-й биполярный признак входного образа и q-го эталона соответственно,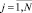 
, 
.
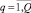Простейшие преобразования R(X, Xq) приводят к тому, что для нахождения k минимизация R(X, Xq) по индексу k – номеру эталона – может быть заменена максимизацией скалярного произведения векторов X и Xq:
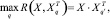
где индекс T означает транспонирование вектора.
Операцию определения скалярного произведения двух векторов реализует нейрон, потенциал которого определяется по формуле
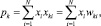
где wki = xki – синаптические коэффициенты k-го нейрона.
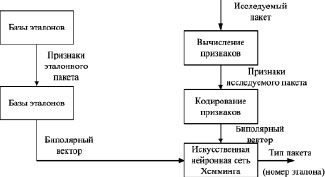
Рис. 3. Схема обработки данных в нейросетевом анализаторе Хемминга ИНС относит объект к классу q′, если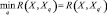 
Значит, характеристики эталонного объекта (образа) хранятся в ИНС Хемминга в форме синаптических коэффициентов нейрона. Для применения нейросетевого классификатора Хемминга необходимо все признаки образа, которые обычно представлены действительными или целыми числами, конвертировать в биполярный код. Тогда N будет означать общее число биполярных разрядов кода всех используемых для распознавания признаков [4].
ИНС Хемминга содержит столько нейронов, сколько эталонных образов хранится в базе данных. Пусть такое число будет обозначаться как M. Предполагается, что при каждой записи в базу эталонных образов (БЭО) нового типового образа выполняется детальное вычисление его вектора признаков. Значит, БЭО содержит не только образы, но и соответствующие векторы действительных чисел Xq = {xq1, xq2, ..., xqN},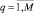 
. Для успешного применения ИНС Хемминга все действительные признаки должны быть представлены своим двоичным кодом. Допустим, что длина кода каждого из признаков xqi, 
, 
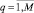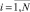, равна J. Тогда общее число двоичных признаков, поступающих на вход ИНС Хемминга, можно обозначить как N0 = JN. Обозначим двоичные признаки y0, 
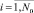. Каждый из M нейронов ИНС Хемминга имеет N0 синаптических коэффициентов, которые представляют код признаков соответствующего эталонного образа в базе данных. Заметим, что в основе эталонных образов хранятся не коды, а действительные числа xqi, 
, 
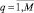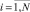. Коды выражаются в процедуре эксплуатации сети Хемминга. Такой подход дает возможность употреблять любую из имеющихся схем кодирования.
Заключение
Рассмотренные модели позволяют сделать вывод, что наилучшим подходом в создании современной системы идентификации ЛВС среднего предприятия является комбинированный подход. Он включает в себя хорошо зарекомендовавшие статистический метод, в дополнение к уже имеющимся сигнатурным системам, а в качестве самообучаемой модели применить нейросетевой анализатор сетевого трафика, основанный на оптимизированной нейросети Хемминга.