Для исполнения страховой компанией обязательств перед клиентами в соответствии с [4, 6] страховщик наряду с резервом незаработанной премии, резервом заявленных, но неурегулированных убытков, стабилизационным резервом формирует резерв произошедших, но незаявленных страховых убытков (далее – РПНУ).
В страховой деятельности РПНУ является источником средств для оплаты требований клиентов, которые будут предъявлены ими в связи с уже произошедшими страховыми случаями и оказывает влияние на налогооблагаемую базу, тарифную политику, платежеспособность, финансовую устойчивость, страховую убыточность и т.п. В связи с этим правильность и точность оценки РПНУ является существенным для страховщика. С одной стороны, заниженная оценка может привести к нехватке средств на страховые выплаты и, следовательно, неплатежеспособности страховой компании, с другой, завышенная оценка требует адекватного размера актива в покрытие резерва [5, 6] и, следовательно, влияет на прибыль страховщика. Таким образом, для страховой компании возникает оптимизационная задача нахождения такого значения РПНУ, при котором общий риск потери дохода, связанный с его формированием, будет минимальным.
В настоящей работе представлена стохастическая имитационная модель поиска оптимальной величины РПНУ страховой компанией, описанная в терминах систем массового обслуживания с построением функционала потерь Φ(T, Imax). В качестве практического применения модели найдены оптимальные значения РПНУ для страхования средств наземного транспорта и страхования средств воздушного транспорта на примере статистических данных страховой компании.
Постановка задачи
Рассмотрим стохастическую имитационную модель оценки резерва произошедших, но незаявленных страховых убытков в виде одноканальной системы массового обслуживания, представленную в статье [1] с отказами.
Пусть на стохастическом базисе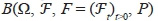 
заданы (At)t≥0 – точечный считающий процесс числа произошедших убытков в момент времени t ≥ 0; (Dt)t≥0 – точечный считающий процесс числа заявленных, но неурегулированных убытков; (Qt)t≥0 – количество произошедших, но незаявленных убытков. При этом At, Dt являются пуассоновскими процессами с компенсаторами
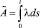и 
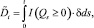
где λ > 0 – интенсивность входящего потока; δ > 0 – интенсивность обслуживания. Пусть заявка, пришедшая в момент времени t, в случае, если на обслуживающем устройстве длина очереди превышает значение Qmax, покидает систему и в дальнейшем в процессе обслуживания не участвует (рис. 1). Для этого введем точечный считающий процесс (Rt)t≥0, обозначающий количество заявок, покинувших систему к моменту времени t в случае выполнения условия Qs ≥ Qmax. Тогда
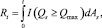(1)
где I{•} – индикаторная функция.
Взаимосвязь процессов At, Dt, Qt, Rt представлена в виде системы массового обслуживания (рис. 1), в которой роль заявок играют произошедшие страховые случаи, входящий и выходящий потоки характеризуются процессами At, Dt соответственно; длина очереди в момент времени t характеризуется процессом Qt, а количество отказов в обслуживании – процессом Rt. Общее балансовое уравнение СМО для определения длины очереди Qt (рис. 2–3) на обслуживающем устройстве может быть записано в виде
Qt = Q0 + At – Dt – Rt, (2)
где Q0 – количество заявок на приборе в момент времени t = 0, A0, D0, R0 = 0.
Пусть ηk > 0 – размер страхового возмещения k-й заявки, отказанной в обслуживании – есть случайная величина с функцией распределения F(ηk ≤ x), где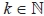 
. Тогда суммарная величина страховых убытков (в у.е.), отказанных в обслуживании, может быть записана в следующем виде:
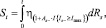(3)
где Imax – предельно допустимый размер РПНУ соответствующего вида страхования.
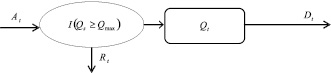
Рис. 1. Общая схема работы СМО
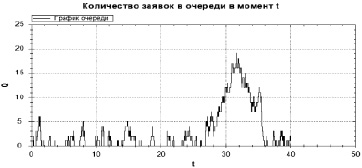
Рис. 2. Пример имитационного моделирования количества произошедших, но незаявленных страховых случаев (процесс Qt) за время T = 40 месяцев для страхования средств наземного транспорта, λ = 0,1420, δ = 0,0925
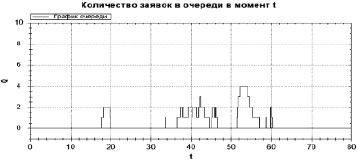
Рис. 3. Пример имитационного моделирования количества произошедших, но незаявленных страховых случаев (процесс Qt) за время T = 60 месяцев для страхования средств воздушного транспорта, λ = 1,83, δ = 0,80
Тогда балансовое уравнение величины РПНУ запишется в виде:
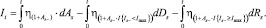(4)
При рассмотрении задачи об оптимальном управлении определим функционал потерь:
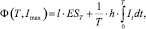(5)
где слагаемое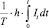 
можно интерпретировать как зарезервированную сумму денежных средств страховой компанией под произошедшие, но незаявленные страховые выплаты, а слагаемое EST – незарезервированная сумма денежных средств под произошедшие, но незаявленные клиентом страховые выплаты. Отсюда возникает задача достаточно сложного компромисса: с одной стороны увеличение слагаемого EST (при Imax > 0) ведет к неисполнению обязательств страховой компанией перед клиентами и, следовательно, ведет к увеличению риска разорения страховой компании. С другой стороны, завышение значения РПНУ (при Imax > ∞) оказывает влияние на прибыль страховщика (потерю дохода) и, следовательно, ведет к возникновению дополнительных рисков для его финансовой устойчивости [4]. Коэффициенты l, h > 0 в выражении (4) характеризуют степень риска потери дохода, разорения страховой компании и определяются экспертно.
Таким образом, в задаче необходимо определить управляемое значение Imax – оптимальное значение величины РПНУ, при котором общий риск потери дохода, связанный со страховой деятельностью, при установленных значениях l, h > 0 является минимальным. Следовательно, необходимо решить задачу оптимального управления в форме
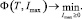(6)
Эксперимент, результаты моделирования
Построим численное решение задачи (5)–(6) для модели СМО (1)–(2) при фиксированном значении λ > 0, δ > 0 с заданной функцией распределения размера страхового возмещения F(η ≤ x). В статье [1] было установлено, что для страхования средств наземного транспорта λ = 0,1420, δ = 0,0925, функция распределения размера страхового возмещения η (в 104 тыс. руб.) имеет логнормальное распределение c параметрами μ = 3,5016, σ2 = 0,93. Для страхования средств воздушного транспорта λ = 1,83, δ = 0,80, функция распределения размера страхового возмещения η имеет логнормальное распределение с параметрами μ = 0,6635, σ2 = 1,5842 (в 105 у.е.).
Для каждой точки 0, Δ, 2•Δ, ..., n•Δ, где n ∈ N0 = {0, 1, 2, ..., N} , Δ – дискретность шага, рассчитаем значение функционала (4) (рис. 1, 2).
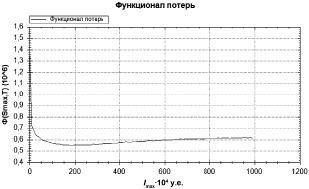
Рис. 4. График Φ(Smax, T) для КАСКО АМ, T = 1000, Δ = 10 тыс. руб., λ = 0,1420, δ = 0,0925, η – log Normal(3,65016; 0,93), l = 1, h = 1
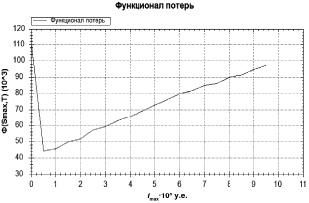
Рис. 5. График Φ(Smax, T) для КАСКО ВС, T = 1000, Δ = 50 тыс. у.е., λ = 1,83, δ = 0,80, l = 1, h = 2
Заключение
Таким образом, была рассмотрена модель поиска оптимального значения резерва произошедших, но незаявленных убытков в семимартингальных терминах систем массового обслуживания. При заданных величинах λ, δ и функции распределения размера страхового возмещения F(η ≤ x), рассчитываемых статистически, и l, h, определяемых экспертно, найден оптимальный размер РПНУ для страхования средств наземного и воздушного транспорта (рис. 4–5).
Вышеуказанная модель может быть использована как альтернативный метод модели расчета РПНУ при составлении финансовой отчетности страховой компании, при выборе оптимальной стратегии резервирования при финансовом планировании страховой деятельности и т.п.