Для развития экономики любого государства необходимо гармоничное развитие сферы финансов и инвестиций. Основную роль в данном направлении играет банковская система. В современных условиях экономическая эффективность деятельности банка основывается на оправданной рыночной стратегии размещения и привлечения ресурсов с точки зрения доходности, ликвидности и минимизации рисков. Эффективность работы банка определяется одним критерием кредитных и депозитных портфелей. Плохое качество портфеля банка напрямую ведет к его банкротству. Равно как умелое управление источниками ресурсов и эффективное распределение их между доступными финансовыми инструментами и направлениями инвестирования (кредиты, ценные бумаги и т.п.) влечет высокую маржу и высокую прибыльность.
Основными принципами формирования инвестиционного портфеля являются надежность и доходность вложений, их стабильный рост и высокая ликвидность. Целью оптимизации портфеля ценных бумаг является формирование такого портфеля ценных бумаг, который бы соответствовал требованиям инвестора или предприятия, как по доходности, так и по возможному риску, что достигается путем распределением ценных бумаг в портфеле. При инвестировании ценных бумаг инвестор формирует портфель этих бумаг и использует для этого наиболее известные и апробированные на практике модели: Марковица [5, 7], Шарпа [8], Тобина [1] и другие. Для решения данных задач можно применить методы квадратичного программирования, метод множителей Лагранжа и др. [9].
Однако все эти методы эффективны только в том случае, если задачи формирования оптимального инвестиционного портфеля сформулированы корректно. На практике многие параметры определяются приближенно, и это приводит к некорректной постановке «возмущенных» оптимизационных задач с характерной для них неустойчивостью и приближенностью полученных решений [2].
В [6, 10–12] авторами данной статьи предложен метод расширения множества допустимых значений для решения «возмущенных» задач распределения и размещения ресурсов и объектов, обеспечивающий нахождение точных и устойчивых решений.
В предлагаемой работе, рассматривающей очередной этап предынвестиционного анализа банков развития [3, 4], метод расширения обобщен для задачи формирования оптимального инвестиционного портфеля банка, которую можно отнести к классу нелинейных оптимизационных задач.
Математическая постановка задачи
Допустим, банк (или другой инвестор) имеет S миллионов долларов, чтобы инвестировать в ценные бумаги компаний из K разных секторов экономики. Каждая компания i из сектора k обязуется платить дивиденды (или проценты) на эти ценные бумаги в течение какого-то периода времени, после чего она обязуется возвратить сумму займа. Допустим компания 1 обязуется платить согласованную квартальную процентную ставку в течение Т1 кварталов на каждый доллар займа. Другая компания обещает платить увеличивающийся процент в течение Т2 кварталов. Третья компания обещает выплатить всю сумму с накопленными процентами через Т3 кварталов и т.д.
Так как компании могут иметь трудности в будущем, то Банк рассматривает эти платежи как случайные величины, которые могут быть больше или меньше, чем обещанные. Задача банка разместить инвестиционные ресурсы так, чтобы избежать или минимизировать риск потери денег с учетом обеспечения планируемого объема дохода от портфеля и приемлемых значений наиболее важных параметров инвестиционного процесса
Формально задача банка может выглядеть следующим образом: минимизация ожидаемой вариации суммы будущих платежей
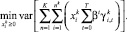 (1)
(1)
С учетом обеспечения ожидаемой величины чистой приведенной стоимости (NPV)
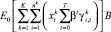 (2)
(2)
и выполнения диверсификационных ограничений
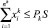 для всех секторов
для всех секторов 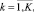 (3)
(3)
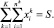 (4)
(4)
В поставленной выше задаче использованы следующие обозначения:
1) 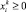 – денежные инвестиции в компанию i из сектора k, где i = 1, 2, …, nk;
– денежные инвестиции в компанию i из сектора k, где i = 1, 2, …, nk;
2) β ∈ (0, 1) – дисконтный фактор, который банк использует, чтобы оценивать платежи из последующих кварталов;
3) индекс T – максимальное количество кварталов, в течение которых по крайней мере какие-нибудь компании должны выплачивать займы (максимальный срок займов);
4) K – количество разных секторов. А число nk – это количество компаний из сектора k, которые банк рассматривает включить в свой портфель;
5) 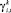 – платеж компании i из сектора k в квартал t. Банк принимает величины
– платеж компании i из сектора k в квартал t. Банк принимает величины 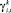 как случайные параметры своей задачи (рыночные процентные ставки);
как случайные параметры своей задачи (рыночные процентные ставки);
6) B – ожидаемая доходность банковского портфеля;
7) Pk – параметр диверсификации, принимающий значение от 0 до 1.
Анализ распределения платежей
При согласовании величин платежей между инвестором и компанией обычно ориентируются не только на индивидуальную составляющую доходности конкретной компании, но и на общую составляющую доходности всего рынка RМ и среднюю доходность компаний соответствующего сектора rk. Следовательно, процентную ставку 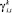 можно разложить следующим образом:
можно разложить следующим образом:
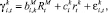 (5)
(5)
где 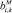 и
и 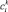 определяют насколько чувствительны доходы компании i из cектора k к изменениям во всем рынке или в отдельном секторе (factor loadings), а
определяют насколько чувствительны доходы компании i из cектора k к изменениям во всем рынке или в отдельном секторе (factor loadings), а 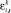 – это индивидуальная составляющая доходности компании i из cектора k. Коэффициенты
– это индивидуальная составляющая доходности компании i из cектора k. Коэффициенты 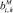 и
и 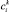 обычно находятся с помощью простой линейной регрессии.
обычно находятся с помощью простой линейной регрессии.
Предположим, что 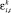 независима от индивидуальных составляющих доходности других компаний, так что для i ≠ j:
независима от индивидуальных составляющих доходности других компаний, так что для i ≠ j:
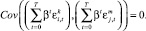
Также предполагается, что 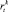 независима от секторных составляющих доходности других секторов, cледовательно для k ≠ m:
независима от секторных составляющих доходности других секторов, cледовательно для k ≠ m:
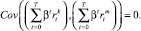
С учетом введенных предположений выражение для ожидаемого значения NPV можно привести к следующему виду:
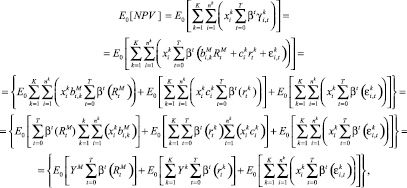
где 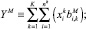
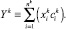
Аналогично преобразуем и выражение для вариации NPV
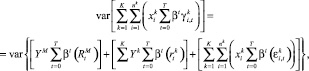
которая в силу предположения о независимости распределений равна
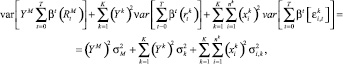
где 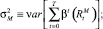
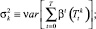
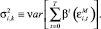
С учетом этих преобразований задача (1)–(4) примет вид
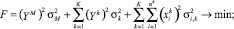 (6)
(6)
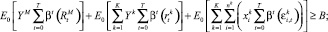 (7)
(7)
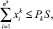
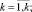 (8)
(8)
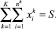 (9)
(9)
Общая схема метода расширения для решения задачи формирования банковского портфеля
Решение выше сформулированной задачи не вызывает затруднений кроме тех случаев, когда платежи компаний характеризуются коэффициентами 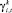 , имеющими незначительные отклонения от некоторого общего их значения. Такая «возмущенность», например, в виде выражения (5) имеет место при составлении многих банковских портфелей. Применение обычных методов квадратичной оптимизации при наличии «возмущенного» ограничения приводит к неустойчивости решения таких задач, поэтому необходима некоторая процедура регуляризации задачи [11]. Ее суть состоит в установлении связи между решениями исходной задачи (6)–(9), которую назовем «возмущенной», и более простой «расширенной» задачей:
, имеющими незначительные отклонения от некоторого общего их значения. Такая «возмущенность», например, в виде выражения (5) имеет место при составлении многих банковских портфелей. Применение обычных методов квадратичной оптимизации при наличии «возмущенного» ограничения приводит к неустойчивости решения таких задач, поэтому необходима некоторая процедура регуляризации задачи [11]. Ее суть состоит в установлении связи между решениями исходной задачи (6)–(9), которую назовем «возмущенной», и более простой «расширенной» задачей:
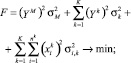 (10)
(10)
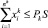
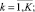 (11)
(11)
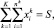 (12)
(12)
полученной из (6)–(9) при исключении ограничения (7).
Установим связь между множествами допустимых решений X и Xрасш, соответственно исходной (6)–(9) и расширенной (10)–(12) задач. Для этого сформулируем две леммы.
Лемма 1. «Допустимое множество решений X исходной задачи (4)–(8) всегда является подмножеством множества решений расширенной задачи (9)–(11), т.е. X ⊆ Xрасш». Справедливость данного утверждения следует из структуры этих задач.
Лемма 2. «Оптимальное решение исходной задачи совпадает с оптимальным решением расширенной задачи только тогда, когда:
1) множества допустимых решений этих задач эквивалентны;
2) оптимальное решение расширенной задачи принадлежит множеству X, т.е. xpасш ∈ X».
Доказательство. Действительно, целевые функции исходной (5) и расширенной (9) задач одинаковы, следовательно, идентичность множеств допустимых решений этих задач приводит к эквивалентности самих задач, а следовательно, и их оптимальных решений. Далее, так как Fpасш = suprenum F, следовательно, ни одно ограничение исходной задачи не может расширить множество, определяемое ограничениями расширенной задачи. Поэтому любой переход от точки xpасш ∈ Xрасш к другой точке x ∈ X будет ухудшать значение целевой функции или, другими словами, этот переход будет означать спуск от Fрасш к другому значению целевой функции.
В соответствии со сказанным приведем следующую общую схему решения задачи формирования оптимального портфеля методом расширения [10]:
1. Решение расширенной задачи.
2. Проверка полученного решения на допустимость по ограничению (7) исходной задачи. Если решение допустимо, то оно оптимально.
3. Выбор направления и шага спуска.
4. Переход к новому решению.
Новое решение, полученное в результате спуска, будет очевидно оптимальным, если спуск в выбранном направлении приводит к наименьшему изменению значения целевой функции по сравнению с другими направлениями.
Главным и определяющим этапом данной схемы является третий этап.
Выбор направления и шага спуска
Пусть решение расширенной задачи xрасш не удовлетворяет всем ограничениям исходной задачи и необходимо перейти к новому решению
x = xрасш + h.
Элементы вектора вычисляются по схеме
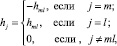
где 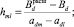 m – индекс элемента вектора xрасш, из которого производится спуск; l – индекс элемента, в который осуществляется спуск; d – индекс нарушенного ограничения вида (7);
m – индекс элемента вектора xрасш, из которого производится спуск; l – индекс элемента, в который осуществляется спуск; d – индекс нарушенного ограничения вида (7); 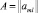 – матрица коэффициентов ограничения вида (7).
– матрица коэффициентов ограничения вида (7).
Для выбора параметров m, l в формуле (13) сформулируем следующее утверждение [6]: «Точка x = xрасш + h является решением задачи (6)–(9) тогда и только тогда, когда параметры m, l определяются из условия
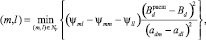
где Ψml – элементы матрицы Y коэффициентов, стоящих перед нелинейной частью целевой функции (6)».
Алгоритм метода расширения для решения задачи формирования банковского портфеля
Шаг 1. Решение расширенной задачи (10)–(12).
Шаг 2. Проверка полученного решения на допустимость по ограничениям (7) исходной задачи. Если решение допустимо, то оно оптимально. В противном случае переход к шагу 3.
Шаг 3. Вычисление значений
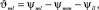
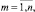
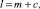
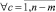
и определение возможных направлений спуска NV из условия
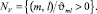
Шаг 4. Определение наилучшего направления спуска:
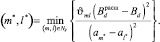
Шаг 5. Вычисление величины шага спуска:
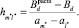
Шаг 6. Переход к новому решению x = xрасш + h и возвращение к шагу 2.
Заключение
На практике используют множество методов формирования оптимальной структуры портфеля ценных бумаг, однако как было сказано выше, все эти методы эффективны только в том случае, если задачи формирования оптимального инвестиционного портфеля сформулированы корректно. В статье проведен анализ распределения платежей и приведена общая схема метода расширения для решения задачи формирования банковского портфеля, с учетом нестабильности и «возмущенности» параметров моделей задач. Так же на основе сформулированных лемм разработан алгоритм метода расширения для решения задачи формирования банковского портфеля, который позволяет инвесторам в условиях быстро развивающейся рыночной экономики повышать эффективность инвестиционной деятельности. Считаем, что представленная модель формирования инвестиционного портфеля банка с возмущенными параметрами и алгоритм её решения являются достаточно универсальными и актуальны не только для реализации государственной стратегии в данном направлении, но и для осуществления коммерческих интересов любого банка, включая и банк развития.



