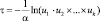На данном этапе развития экономики во многих отраслях промышленности применяются гибкие производственные системы, которые позволяют переходить с одного вида продукции на другой с минимальными затратами времени и труда. Данные системы требуют значительных капиталовложений, поэтому важным моментом при их внедрении является правильная оценка их качества работы и эффективности функционирования. Риск получения отрицательного эффекта от инвестирования гибкой автоматизации предъявляет особые требования к качеству и эффективности работы гибких производственных систем (ГПС).
Качество производственных систем достигается единым комплексом решений при его проектировании, подборе номенклатуры продукции и разработке технологии ее изготовления, при диспетчеризации и управлении технологическими процессами. Поиск оптимальных решений возможен лишь с помощью компьютерного моделирования производственного процесса при различных значениях аргументов из интервалов их допустимых значений и оценки получаемых вариантов решений по выбранным критериям.
Основными задачами, влияющими на эффективность функционирования производственной системы, являются задачи распределения и размещения ресурсов оборудования в условиях сложной структуры ГПС и нестационарности технологических процессов и параметров системы и возможности переразмещения транспортных средств и магазинов инструментов.
Функциональная структура комплекса для моделирования работы ГПС
Структура комплекса для моделирования работы ГПС определяется характером и взаимосвязью задач, реализуемых в производственной системе, среди которых основными являются [3]:
- расчет интервалов рекомендуемых значений ряда параметров ГПС. Результаты решения этой задачи могут использоваться при укрупненном расчете на ранних стадиях проектирования или служить исходными данными при запуске блока моделирования работы ГПС;
- расчет количества оборудования на производственном участке;
- определение типа и количества транспортных средств;
- формирование вариантов сменного задания.
Таким образом, программный комплекс должен состоять из двух основных блоков (блок диспетчеризации и блок моделирования) и ряда вспомогательных (информационный блок, блок помощи, блок настройки параметров, сервисный блок и т.д.). Структура комплекса показана на рисунке.
Блок диспетчеризации реализует следующие задачи:
- расчет оптимальных значений параметров сменного задания;
- корректировка сменного задания;
- оптимизация исходного размещения инструмента и местоположения транспортных средств;
- выдача оперативной информации о ходе производства.
Блок моделирования производственных процессов описывает ход выполнения ГПС предписанного сменного задания. Результатами работы блока являются показатели эффективности работы оборудования, транспортных средств и использования инструмента. Моделирование осуществляется на уровне технологического перехода, т.е. учитываются простои из-за автоматической доставки, смены инструмента и подготовки его к работе.
Моделирующий алгоритм строится на основе определения моментов изменений состояния в работе моделируемых устройств, регистрации изменений и их последующей статистической обработке. В основу алгоритма положены модели и методы распределения ресурсов, а также аппарат имитационного моделирования случайных параметров и процессов.
Информационный блок обеспечивает выдачу оперативной информации о ходе решения задач и предоставляет пользователю результаты решения. Блок помощи содержит подсказки по вводу данных и инструкции о работе с программным комплексом.
Формулы моделирования основных теоретических распределений случайных величин
|
Распределение |
Функции плотности |
Формула для моделирования |
|
Нормальное |
|
|
|
Равномерное |
|
|
|
Экспоненциальное |
|
|
|
Линейное |
|
|
|
Гамма |
|
|
Математические модели и методы решения задач блока диспетчеризации
Для решения задач блока диспетчеризации предлагается использовать алгоритмы, обеспечивающие поиск устойчивых оптимальных решений в условиях возможной некорректности математической постановки задач [5].
Рассматривается задача распределения ресурсов S между параллельно работающими однотипными агрегатами, точные значения параметров которых неопределенны (стохастическая модель).
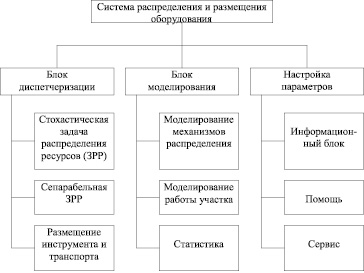
Структура комплекса
Математическая модель такой задачи имеет вид
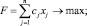
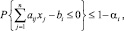
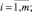
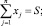
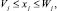
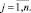
Предполагается, что каждое ограничение выполняется с минимальной вероятностью (1 – αi), 0 ≤ αi ≤ 1, а все коэффициенты cj, aij, bi являются случайными величинами с различными законами распределения и известными значениями математического ожидания и дисперсии. Алгоритм решения задачи приведен в [2]. Для моделирования значений cj, aij, bi можно воспользоваться формулами, приведенными в таблице, или одним из методов генераций случайных величин, например методом обратной функции [4].
В данном блоке также реализован алгоритм решения сепарабельной задачи распределения ресурсов, математическая постановка которой имеет вид
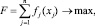
при ограничениях
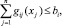
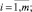
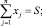
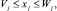
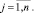
Здесь все функции fj(xj), gij(xj) являются сепарабельными.
Для определения оптимального размещения инструментов и транспортных средств используются две политики:
а) политика глобального оптимума, минимизирующая транспортные расходы за полное время выполнения сменного задания, и формируется следующим образом:
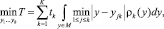
где yk – местоположение k-го магазина инструментов или транспортного средства;
б) политика близорукого оптимизма, позволяющая получить размещение дополнительного транспортного средства или магазина инструментов таким образом, что результирующая конфигурация является оптимальной для текущего режима работы и формируется следующим образом:
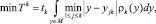
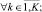
здесь М – компакт, выпуклое множество.
Также для определения оптимального размещения инструментов и транспортных средств можно использовать метод расширения [5].
Математические модели, методы и алгоритмы решения задач блока моделирования
Типичной схемой распределения ресурсов в условиях неполной информированности органа распределения является распределение на основе заявок потребителей. Пусть zi – заявка потребителя с номером i на ресурс. На основе полученных заявок z = (z1, z2, ..., zn) центральный орган системы распределяет ресурс S согласно некоторому принципу распределения
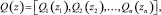
таким образом, что
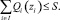
Тогда математическую модель задачи распределения ресурсов можно представить в виде
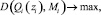
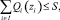
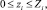 i ∈ I.
i ∈ I.
Здесь 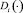 - функция максимального дохода i-го элемента системы, а Mi - количество ресурса, обеспечивающее максимальный эффект элементу i.
- функция максимального дохода i-го элемента системы, а Mi - количество ресурса, обеспечивающее максимальный эффект элементу i.
Блок моделирования предполагает использование следующих механизмов распределения ресурсов [1]:
а) механизм прямых приоритетов:
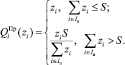
Так как ресурс распределяется пропорционально поданной заявке, то при механизме прямых приоритетов возникает тенденция к завышению заявок на ресурс. Заметим, что эта тенденция не зависит от степени дефицита. Следовательно, механизм прямых приоритетов нельзя считать эффективным в условиях дефицита ресурса, хотя в условиях избытка ресурса данный механизм может быть достаточно полезным.
Алгоритм механизма прямых приоритетов состоит из шагов [1]:
Шаг 1. Вычисление суммарного количества заявленного ресурса
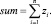
Шаг 2. Если sum ≤ S, то Zi = zi, 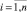 , иначе
, иначе
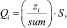
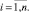
Шаг 3. Вывод результатов решения;
б) механизм обратных приоритетов:

где Ai, i ∈ N – некоторые константы. Величина характеризует потери организационной системы, если i-й потребитель вообще не получит ресурса. Тогда отношение Ai/si определяет удельный эффект от использования ресурса.
Здесь приоритет потребителя при распределении тем выше, чем меньшее количество ресурса он заказывает. Механизм обратных приоритетов является эффективным и в условиях избытка, и в условиях дефицита ресурса. А в ряде случаев позволяет получить и оптимальное распределение ресурсов.
Алгоритм механизма обратных приоритетов включает следующие шаги:
Шаг 1. Вычисление суммарного количества заявленного ресурса
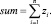
Шаг 2. Если sum ≤ S, то переход к шагу 3, иначе к шагу 4.
Шаг 3. Вычисление и вывод значений
Qi = zi, 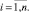
Шаг 4. Если 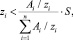 то Qi = zi, иначе
то Qi = zi, иначе
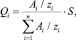
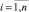 ;
;
в) механизм открытого управления:
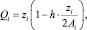
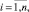
где 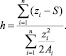
Механизм открытого управления выражает идею согласования интересов органа распределения и потребителей. При согласованном управлении заметна тенденция потребителей сообщать более достоверные оценки.
Укрупненный алгоритм решения задачи распределения с помощью механизма открытого управления состоит из шагов:
Шаг 1. Формирование цены за ресурс
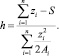
Шаг 2. Вычисление значения ресурса, распределенного потребителю
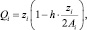
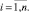
Заключение
Предложенная укрупненная структура блоков комплекса не охватывает всех задач ГПС, однако реализованные в них алгоритмы позволяют решить одну из важнейших производственных задач, а именно получение устойчивых оптимальных решений в условиях некорректности математической постановки задач, а также в условиях неточного задания параметров ГПС.




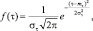 –∞ < τ < ∞
–∞ < τ < ∞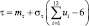
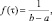 τ ∈ [a, b]
τ ∈ [a, b]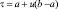
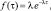 τ ≥ 0
τ ≥ 0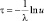
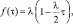
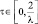
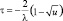
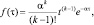 α > 0, k > 0, τ ≥ 0
α > 0, k > 0, τ ≥ 0