Современные инфокоммуникационные системы широко используют системы на кристалле (СнК), которые на основе применения математической модели ортогонального частотного мультиплексирования (OFDM) позволяют обеспечить высокую помехоустойчивость, передачу информации в реальном масштабе времени, устойчивость к многолучевому распространению радиоволн и ряд других преимуществ. Однако использование математической модели цифровой обработки сигналов (ЦОС) на основе быстрых преобразований Фурье (БПФ) в позиционной системе счисления не позволяет в полной мере использовать весь потенциал сигнального процессора. Обеспечить предельную производительность спецпроцессора ЦОС можно за счет использования параллельных методов вычислений. Но усиливающаяся тенденция к использованию параллельных вычислений, с другой стороны, приводит к снижению надежности работы вычислительной системы. Решить данное противоречие можно за счет использования алгебраических структур корректирующих непозиционных модулярных кодов. Параллельная и независимая обработка малоразрядных остатков, их функциональная равнозначность позволяют не только повысить скорость вычислений, но и обеспечить СП свойство устойчивости к отказам.
Поэтому разработка новой математической модели многоверсионных корректирующих модулярных кодов, используемых для выполнения ЦОС, является актуальной задачей.
Основная часть. Цель исследования
Современный этап развития беспроводных инфокоммуникационных систем характеризуется широким применением в средствах связи микропроцессорных систем специального назначения. При этом каждая из сфер применения спецпроцессоров (СП) предъявляет свои специфические требования к составу и структуре вычислительного устройства. По мере развития сетей и систем передачи данных наблюдается тенденция – повышение требований к скорости передачи информации, надежности и качеству предоставляемых сервисов. Это приводит к активизации работы по разработке новых принципов организации радиосвязи.
В последние годы наблюдается повышенный интерес к применению перспективных видов сигнально-кодовых конструкций OFDM (Orthogonal Frequency Division Multiplexing). При этом в основе метода OFDM положено быстрое преобразование Фурье (БПФ). Использование математической модели цифровой обработки сигналов на основе БПФ позволяет эффективно бороться с многолучевостью, которая является характерной чертой радиосвязи. В качестве достоинств OFDM можно выделить достаточно высокий коэффициент использования выделенного частотного спектра и отсутствие межсимвольной интерференции [8–10].
Однако наряду с достоинствами системы передачи и обработки с OFDM, использующие математическую модель ортогонального частотного мультиплексирования на основе БПФ, имеют ряд проблемных сторон. К ним можно отнести:
– недостаточно высокая скорость ортогонального преобразования сигнала;
– увеличение сложности модема OFDM, что приводит к снижению его надежности.
Устранить данные недостатки можно за счет обеспечения свойства устойчивости к отказам во время функционирования СП ЦОС.
Поэтому целью данной работы является повышение отказоустойчивости быстродействующих спецпроцессоров ЦОС на основе использования новой математической модели многоверсионных корректирующих модулярных кодов.
Материалы и методы исследования
Очевидно, что для достижения поставленной цели решающую роль играет алгебраическая система, используемая при реализации математической модели OFDM. Она должна обеспечить как максимальную производительность выполнения ортогональных преобразований сигналов, так и способность корректировать ошибки, вызванные сбоями и отказами оборудования. Такими свойствами обладают непозиционные коды классов вычетов.
Использование модулярных кодов позволяет повысить эффективность реализации ЦОС за счет перехода от обработки одномерных сигналов к обработке многомерных сигналов, используя изоморфизм, порожденный китайской теоремой об остатках (КТО). Применение данных алгебраических систем позволяет провести распараллеливание на уровне выполнения математических операций. В настоящее время наибольшее применение нашли система остаточных классов (СОК) и полиномиальная система классов вычетов (ПСКВ).
В системе остаточных классов целое число A представляется в виде совокупности остатков, A = (a1, a2, ..., an), где A ≡ ai modpi; i = 1, 2, …, n, полученных путем его деления на попарно взаимно простые модули pi [6–7]. Основным достоинством СОК является высокая скорость выполнения модульных операций, к которым относятся сложение, вычитание и умножение. Тогда, используя СОК, можно реализовать дискретное преобразование Фурье
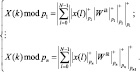(1)
В ПСКВ полиномиальная форма числа представляется в виде остатков от деления, только в качестве оснований здесь применяются неприводимые полиномы. В работах [1–3] показано, что применение системы ПСКВ, в которой в качестве оснований используются минимальные многочлены p1(z), p2(z), ..., pn(z), позволяет осуществлять ДПФ в виде
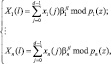(2)
где xi(j) ≡ x(j) mod pi(z);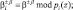 
Xi(l) ≡ X(l) mod pi(z); b – первообразный корень; x(j) – входная последовательность сигнала; X(l) – спектральные составляющие входного сигнала; d = 2v – 1 – размерность входного вектора.
Анализ выражений (1)–(2) показывает, что использование модулярных кодов позволяет операции сложения, вычитания и умножения свести к операциям над остатками. При этом эти операции проходят параллельно и независимо в каждом вычислительном тракте.
Однако переход к параллельным вычислениям приводит к увеличению схемных затрат, что негативно влияет на надежность работы таких устройств ЦОС. Перспективным путем разрешения данного противоречия является придание процессорам свойства отказоустойчивости. Применение модулярных кодов позволяет решить эту задачу при меньших схемных затратах по сравнению с классическим методом маскирования отказов «2 из 3».
Для коррекции ошибок с помощью модулярных кодов вводят r избыточных оснований pn+1(z), ..., pn+r(z), для которых справедливо
deg p1(z) ≤...≤ deg pn–1(z) ≤ deg pn(z) ≤ deg pn+1(z) ≤...≤ deg pn+r(z), (3)
где deg pi(z) – степень неприводимого полинома pi(z); n – количество рабочих оснований.
Код ПСКВ считается разрешенным, если он принадлежит рабочему диапазону
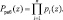(4)
Введение избыточных модулей приводит к появлению полного диапазона кода
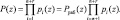(5)
Ошибка, преобразуя правильную комбинацию A = (α1(z), α2(z), ..., αn+r(z)) в комбинацию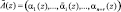 
, осуществляет перевод кода за пределы рабочего диапазона, где αi ≡ A mod pi; 
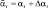– искаженный остаток СОК; Δαi – глубина ошибки.
Так как модулярные коды относятся к непозиционным кодам, то для коррекции ошибки в этих кодах используются позиционные характеристики (ПХ). Они показывают расположение ошибочной кодовой комбинации модулярного кода относительно рабочего диапазона системы. В работе [1] приведен алгоритм и схемная реализация вычисления интервального номера, физический смысл которой определяется как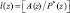 
. Если код ПСКВ не содержит ошибки, т.е. deg A(z) < deg Pраб(z), то значение интервального номера равно нулю, т.е. l(z) = 0. При возникновении ошибки в коде ПСКВ – l(z) ≠ 0. В работе [5] в качестве ПХ используются старшие коэффициенты обобщенной полиадической системы. В работе [4] предлагается для коррекции ошибок применять алгоритм расширения оснований ПСКВ. Однако, отмеченные выше алгоритмы требуют значительных схемных и временных затрат. Уменьшить их можно за счет использования ПХ – усеченной свертки.
Для перевода из ПСКВ в позиционную систему счисления (ПСС) используют
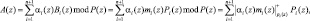(6)
где Bi(z) – ортогональный базис; Pi(z) = P(z)/pi(z); mi(z) – вес базиса; Bi(z) ≡ 1 mod pi(z).
Пусть ошибка произошла по j-му основанию ПСКВ, а ее глубина равна Δαj(z). Произведем перевод ошибочного кода ПСКВ в ПСС
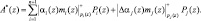(7)
Анализ (7) показывает, что выход за пределы рабочего диапазона Pраб(z) определяется вторым слагаемым. Для выполнения коррекции необходимо вычислить для каждого основания ПСКВ величину Pi(z). Затем вычислим степень рабочего диапазона
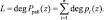(8)
В полиномах Pi(z) отбрасываем разряды, степень которых будет меньше значения
L – deg pi(z) = Li. (9)
Тогда остаются полиномы
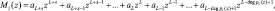(10)
где aj = {0, 1} элементы поля Галуа GF(2).
Если код A(z) = (α1(z), α2(z), ..., αn+1(z)) не содержит ошибки, то его степень deg A(z) < deg Pраб(z) = L. В этом случае свертка произведений остатков αi(z), веса базиса mi(z) и констант Mi(z) должна быть равна нулю
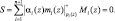(11)
Если код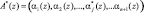 
содержит ошибку, то свертка равна
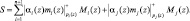(12)
Используя равенство (11), получаем
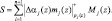(13)
По величине S можно однозначно определить местоположение ошибки и ее глубину.
Результаты исследования и их обсуждение
Пусть рабочими основаниями выбраны многочлены p1(z) = z+ 1; p2(z) = z3 + z+ 1, а контрольным – p3(z) = z3 + z2+ 1. Тогда рабочий диапазон
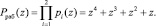
Значит, L = deg Pраб(z) = 4. Вычислим константы
P1(z) = z6 + z5 + z4 + z3 + z2 + z + 1;
P2(z) = z4 + z2 + z + 1; P3(z) = z4 + z3 + z2 + 1.
Вычислим значения весов первого ортогонального базиса. Для этого определяем
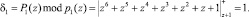
Значит, m1(z) = 1, так как δ1(z)m1(z) ≡ 1 mod pi(z). Вычислим вес базиса B2(z). Получаем
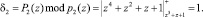
Так как δ2(z) = 1, тогда m2(z) = 1. Для базиса B3(z) получаем
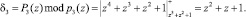
Так как значение δ3(z) ≠ 1, то вес B3(z) равен m3(z) = z2 + 1. Это определяется из условия
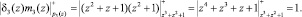(14)
Воспользуемся выражением (10) и вычислим константы Mi(z). Так как deg p1(z) = 1, то имеем
M1(z) = z6 + z5 + z4.
Так как deg p2(z) = 3, то имеем
M2(z) = z4 + z2.
Так как deg p3(z) = 3, то имеем
M3(z) = z4 + z3 + z3.
Пусть на вход блока коррекции подается код ПСКВ
A(z) = z3 + z3 + z + 1 = (0, z2, z).
Так как deg A(z) < deg Pраб(z) = 4, то ПСКВ не содержит ошибки. Произведем вычисление свертки. Определим произведения αi(z) и mi(z). Получаем
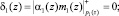
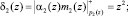
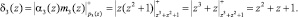
Определим значения δi(z)Mi(z). Получаем
δ1(z)M1(z) = 0(z6 + z5 + z4) = 0;
δ2(z)M2(z) = z2(z4 + z2) = z6 + z4;
δ3(z)M3(z) = (z2 + z + 1)(z4 + z3 + z2) = z6 + z4 + z2.
Оставляем только степени, которые не меньше L = 4. Получаем усеченные значения K1 = 0; K2 = z6 + z4; K3 = z6 + z4. Складываем по модулю два усеченных значения
S = K1 + K2 + K3 = 0+ (z6 + z4) + (z6 + z4) = 0.
Так как свертка S = 0, то код ПСКВ не содержит ошибки.
Пусть ошибка произошла по первому основанию, а ее глубина равна Δα1(z) = 1. Тогда
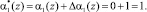
Значит код ПСКВ равен
A*(z) = (1, z2, z) = z6 + z5 + z4.
Тогда имеем
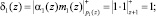
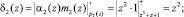
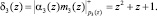
Определяем произведение δi(z)Mi(z). Получаем
δ1(z)M1(z) = z6 + z5 + z4;
δ2(z)M2(z) = z2(z4 + z2) = z6 + z4;
δ3(z)M3(z) = z6 + z4 + z2.
Тогда усеченные значения
K1(δ1(z)M1(z)) = z6 + z5 + z4;
K2(δ2(z)M2(z)) = z6 + z4;
K3(δ3(z)M3(z)) = z6 + z4.
Тогда свертка равна
S = K1 + K2 + K3 = (z6 + z5 + z4) + (z6 + z4) + (z6 + z4) = z6 + z5 + z4.
Так как S ≠ 0, то код ПСКВ содержит ошибку.
В таблице приведены S и соответствующих ей ошибок по рабочим основаниям.
После преобразования из кода ПСКВ в код ПСС проведем исправление ошибки
A(z) = A*(z) + Δ(z) = (z6 + z5 + z4) + (z6 + z5 + z4 + z3 + z2 + z + 1) = z3 + z2 + z + 1.
В отличие от других алгоритмов вычисления ПХ данный алгоритма коррекции ошибок можно применять при построении отказоустойчивых СП ЦОС класса вычетов, способных сохранять работоспособное состояние за счет реконфигурации структуры.
Значения усеченных сверток S
|
Основания |
Ошибка Δαi(z) |
Свертка S |
Корректирующее значение Δ |
|
p1(z) = z + 1 |
1 |
z6 + z5 + z4 |
z6 + z5 + z4 + z3 + z2 + z + 1 |
|
p2(z) = z3 + z + 1 |
1 z z2 |
z4 z5 z6 + z4 |
z4 + z2 + z + 1 z5 + z3 + z2 + z z6 + z4 + z3 + z2 |
Заключение
В работе показана возможность использования модулярных кодов в информационных системах передачи и обработки сигналов. Распараллеливание вычислений на уровне арифметических операций позволяет обеспечить максимальную производительность СП ЦОС. Однако при этом снижается надежность вычислительных устройств. Для обеспечения отказоустойчивости предлагается использовать корректирующие модулярные коды. Разработан алгоритм поиска и коррекции ошибки, который использует усеченную свертку старших разрядов ортогональных базисов. Данный алгоритм позволяет обнаруживать и исправлять ошибки в СП ЦОС, который при возникновении отказов производит реконфигурацию структуры.