Геометрия оболочки вращения
В декартовой системе координат оxуz положение точки М срединной поверхности оболочки вращения определяется радиус-вектором
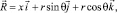(1)
где r – радиус вращения точки М относительно оси ox;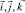 
– орты декартовой системы координат; θ – угол, отсчитываемый от вертикального диаметра против часовой стрелки.
Векторы локального базиса точки М определяются выражениями
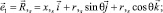
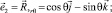
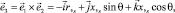(2)
где r,s = r,xx,s – производная радиуса вращения по дуге меридиана s.
Cсоотношение (2) можно представить в матричном виде:
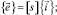
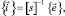(3)
где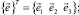 
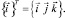
Дифференцированием (1) при использовании (3) можно получить производные векторов (2) в базисе этих же векторов
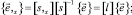
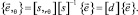(4)
Радиус-вектор произвольной точки оболочки Mς, отстоящей на расстоянии ς от срединной поверхности имеет вид
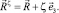(5)
Базисные векторы точки Mς определяются дифференцированием (5) с учетом (4)
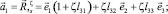
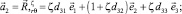(6)
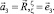
Точка Mς под действием на оболочку заданной нагрузки займет положение Mς*, которое определяется вектором 
, представляемым компонентами в базисе точки M
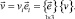(7)
Производные вектора (7) определяются дифференцированием с учетом (4):
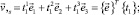
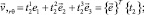
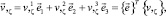(8)
где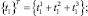 
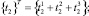
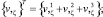
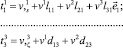– функции компонент вектора перемещения и их производных.
Ковариантные компоненты тензора деформации определяются выражениями [5]
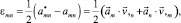(9)
где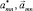 
– ковариантные компоненты метрических тензоров в деформированном и исходном состояниях.
С использованием (6) и (8) соотношение (9) можно представить в матричном виде
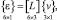(10)
где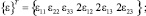 
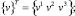[L] – матрица алгебраических и дифференциальных операторов.
Закон Гука
Соотношения между напряжениями и деформациями принимаются в виде [3]
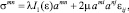(11)
где σmn – контравариантные компоненты тензора напряжений; εmn – ковариантные компоненты тензора деформаций; λ, μ – параметры Ламе; amn – контравариантные компоненты метрического тензора; I1(ε) = εmn amn – первый инвариант тензора деформаций.
Соотношение (11) можно записать в матричном виде
{σ} = [D]{ε}, (12)
где {σ}T = {σ11 σ22 σ33 σ12 σ13 σ23}.
Матрица жесткости шестигранного конечного элемента
Объёмный конечный элемент, принимается в координатной системе x, θ, ς в виде шестигранника с узлами i, j, k, l на нижней грани по координате ς и узлами m, n, p, h по верхней грани [1–4, 6]. Для выполнения численного интегрирования шестигранник отображается на куб с локальными координатами a, b, c, изменяющимися в пределах –1 ≤ a, b, c ≤ 1, с использованием трилинейных функций
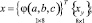
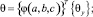
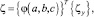(13)
где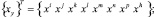 
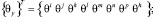
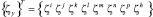– матрицы-строки глобальных координат узлов шестигранника.
Дифференцированием (13) определяются производные глобальных координат в локальной системе x,a, x,b, x,c, θ,a, θ,b, θ,c, ς,a, ς,b, ς,c и локальных координат в глобальной системе a,x, a,θ, a,ς, b,x, b,θ, b,ς, c,x, c,θ, c,ς.
Вектор перемещения внутренней точки конечного элемента определяется выражением
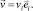(14)
Аппроксимация компонент вектора перемещения (14) через узловые неизвестные выполнялась в двух вариантах.
Скалярная аппроксимация компонент вектора перемещения
Узловые неизвестные конечного элемента перемещения и их производные представляются в локальной и глобальной системах матрицами-строками
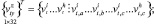
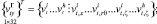
t = 1, 2, 3. (15)
Узловые величины (15) связаны матричной зависимостью
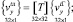(t = 1, 2, 3), (16)
где элементами матрицы [T] являются производные глобальных координат x, θ, ς в локальной системе a, b, c для узловых точек конечного элемента.
Каждая компонента вектора перемещения внутренней точки конечного элемента аппроксимируется через узловые значения этой же компоненты матричным выражением
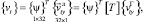(17)
где {ψ}T – аппроксимирующая матрица, элементами которой являются полиномы Эрмита третьей степени.
На основе скалярной аппроксимации (17) выражение (10) представляется в матричном виде
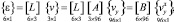(18)
где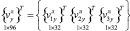 
– строка узловых неизвестных шестигранного конечного элемента;
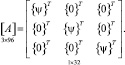
Векторная аппроксимация перемещений
В качестве узловых неизвестных конечного элемента принимаются векторы перемещений узловых точек и их первые производные в локальной и глобальной системах координат и представляются матрицами-строками
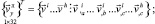(19)
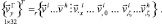
Между столбцами (19) имеет место матричное соотношение
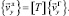(20)
Вектор перемещения внутренней точки конечного элемента аппроксимируется через узловые неизвестные (19) матричной зависимостью
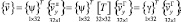(21)
где
γt = ψt;
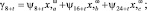
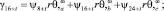
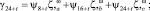
ω = i, j, k, l, m, n, p, h;
t = 1, 2, ..., 8. (22)
Производные вектора перемещения внутренней точки конечного элемента определяются дифференцированием (21)
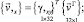
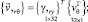
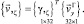(23)
Столбец узловых неизвестных в глобальной системе координат на основе (7) и (8) можно представить матричным соотношением
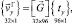(24)
где
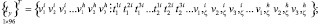(25)
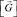– матрица, ненулевыми элементами которой являются базисные векторы узловых точек конечного элемента 
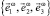(ω = 1, 2, ..., 8).
На основании соотношений (3) можно базисные векторы узловых точек выразить через базисные векторы рассматриваемой внутренней точки конечного элемента
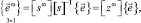(26)
где [sω] – матрица, элементы которой определяются параметрами узловой точки ω.
После замены на основе (26) базисных векторов узловых точек в матрице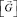 
аппроксимирующие матрицы (21) и (23) можно представить матричными соотношениями
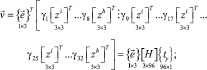
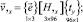
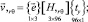
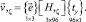(27)
Приравнивая правые части выражений (7), (8) и (27), можно получить аппроксимирующие выражения для компонент вектора перемещения внутренней точки конечного элемента
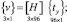
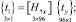
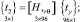
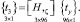(28)
С использованием (28) деформации (10) во внутренней точке конечного элемента определяется матричным выражением
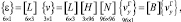(29)
где использовано преобразование
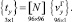
С использованием соотношений (18), (29) и (12) по алгоритму [1] формируется матрица жесткости конечного элемента
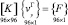(30)
в двух вариантах: на основе скалярной аппроксимации перемещений и на основе векторной аппроксимации. Символом {F} обозначен вектор узловых сил конечного элемента.
Пример. Рассматривалась усечённая эллипсоидная оболочка (рисунок), находящаяся под действием внутреннего давления интенсивности q. Были приняты следующие исходные данные: b– = 0,1 м; t = 0,01 м; rk = 0,005 м; Е = 2·105 МПа; ν = 0,3; h = 0,01 м; q = 2,5 МПа.
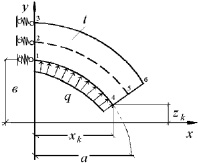
Усеченный эллипсоид вращения, загруженный внутренней равномерно распределенной нагрузкой
Расчеты выполнялись для трех усеченных оболочек с размерами больших полуосей а = 0,5 м; а = 1,0 м; а = 1,5 м. Остальные размеры остались неизменными.
Меридиональные напряжения в точках 1, 2, 3 оказались практически равными для всех оболочек и при каждом варианте аппроксимации перемещений в конечном элементе (σss = 123,5 МПа), что примерно на 0,344 % отличалось от числовых значений меридиональных напряжений, полученных из уравнения равновесия
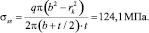
Оказались равными и значения окружных напряжений σθθ в точках 1, 2, 3 для обоих вариантов аппроксимации перемещений в конечном элементе.
|
а, м |
σθθ, МПа |
σθθ, МПа |
σθθ, МПа |
δsk, % |
δb, % |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
0,5 |
45,32 |
49,97 |
51,45 |
11,9 |
2,9 |
|
0,1 |
21,42 |
26,64 |
27,90 |
23,20 |
4,5 |
|
1,5 |
15,51 |
19,94 |
20,83 |
25,5 |
4,2 |
В таблице приведены окружные напряжения в точках 5 (на срединных поверхностях оболочек на правом краю). В первой колонке приведены значения полуосей а усеченных оболочек. Во второй колонке приведены окружные напряжения, полученные при использовании скалярной аппроксимации перемещений конечного элемента. В третьей колонке даются окружные напряжения в точках 5, полученные при использовании векторной аппроксимации перемещений. В четвертой колонке даются окружные напряжения, полученные по равенству Лапласа (в данном случае приближенному)
где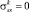 
на правом краю оболочки; 
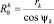– радиус вращения в концевой точке; ψk – угол наклона касательной к отчетному меридиану в концевой точке. Окружные напряжения из соотношения Лапласа определяются выражением
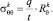
В колонке 5, 6 таблицы приведены расхождения между значениями окружных напряжений.
δsk – расхождения между числовыми значениями напряжения колонки 2 и колонки 4; δb – расхождения между числовыми значениями напряжения колонки 3 и колонки 4.
Как видно значения окружных напряжений, полученные при использовании векторной аппроксимации перемещений (колонка 4) находятся в гораздо лучшем соответствии с результатами, полученными на основе соотношения Лапласа.
Работа выполнена при финансовой поддержке РФФИ (грант № 15-41-02346/16).