Выполнение математических операций с функциональными зависимостями, их сравнение, сложение или перемножение возможно, лишь когда представленные значения находятся в нормированном виде. В табл. 1 приведены усредненные значения основных эксплуатационных свойств макроуровня композиционных материалов (КМ). В табл. 2 приведены нормированные значения показателей качества КМ. В качестве нормальных значений взяты аналогичные свойства товарного тяжелого бетона [3–6].
Нормирование свойств выполнено по методике:
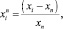 (1)
(1)
где 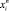 – нормированное значение текущего свойства КМ; xi – абсолютное значение текущего свойства КМ; xn – нормальное значение текущего свойства, за которое принято значение данного свойства тяжелого бетона.
– нормированное значение текущего свойства КМ; xi – абсолютное значение текущего свойства КМ; xn – нормальное значение текущего свойства, за которое принято значение данного свойства тяжелого бетона.
Таблица 1
Усредненные значения показателей качества КМ
|
№ п/п |
Показатели |
Бетон |
ЭКМ |
ГГКМ |
|
1 |
Средняя плотность, кг/м3 |
2350 |
4550 |
4600–7550 |
|
2 |
Предел прочности при сжатии, МПа |
22 |
120 |
50 |
|
3 |
Пористость, % |
7 |
4 |
10 |
|
4 |
Водопоглощение, % |
7 |
0,35 |
0,96 |
|
5 |
Усадка, % |
0,15 |
0,08 |
0,3 |
|
6 |
Морозостойкость, циклов |
200 |
500 |
350 |
|
7 |
Коэффициент водостойкости |
0,9 |
0,85 |
0,9 |
|
8 |
Коэффициент химической стойкости в растворах кислот, щелочей и солей |
0,8 |
0,9 |
0,9 |
|
9 |
Коэффициент радиационной стойкости |
0,8 |
0,95 |
0,9 |
|
10 |
Коэффициент линейного ослабления g-излучения (Eg = 0,6 МэВ), см–1 |
0,15 |
0,33 |
0,5–0,7 |
Таблица 2
Нормированные значения показателей качества КМ
|
Номер показателя |
Бетон |
ЭКМ |
ГГКМ |
ЭКМ норм. |
ГГКМ норм. |
|
1 |
2,35 |
4,55 |
7,55 |
–0,9361702 |
–2,21276596 |
|
2 |
2,2 |
1,2 |
5 |
0,45454545 |
–1,27272727 |
|
3 |
5 |
4 |
10 |
0,2 |
–1 |
|
4 |
7 |
3,5 |
7 |
0,5 |
0 |
|
5 |
1 |
0,8 |
3 |
0,2 |
–2 |
|
6 |
2 |
5 |
3,5 |
–1,5 |
–0,75 |
|
7 |
9 |
8,5 |
9 |
0,05555556 |
0 |
|
8 |
8 |
9 |
9 |
–0,125 |
–0,125 |
|
9 |
8 |
8,5 |
9 |
–0,0625 |
–0,125 |
|
10 |
1,5 |
3,3 |
7 |
–1,2 |
–3,66666667 |
Примечание. ЭКМ – эпоксидный композит, ГГКМ – глетглицериновый композит.
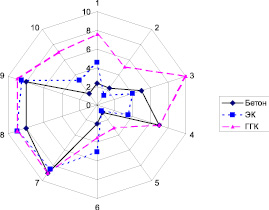
Рис. 1. Лепестковая диаграмма усредненных значений показателей качества КМ
На рис. 1, 2 показаны лепестковые диаграммы основных эксплуатационных свойств КМ и бетона в абсолютных и нормализованных значениях соответственно.
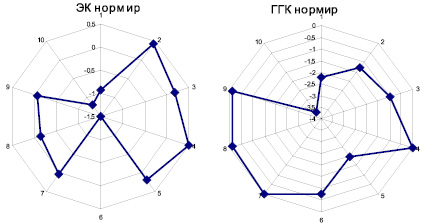
Рис. 2. Лепестковые диаграммы показателей качества КМ, построенные в нормализованном виде
Таблица 3
Группирование показателей КМ
|
№ п/п |
Показатели |
Факторы |
Функции |
|
|
А |
1. |
Средняя плотность – ρ |
ρf, ρs, νf, C, П, Sуд, Рпр, t, Т |
R(νf, C), R(Рпр), ρ(νf, C), r(Рпр), R(t), R(П(ρ(νf, C))), R(T), R(νf, Sуд) – f(A) |
|
2. |
Предел прочности – Rсж, Rиз |
|||
|
В |
3. |
Пористость – П |
νf, Sуд, C, Рпрес, r, Rср, t |
П(νf, C), П(Рпр), П(r(νf, C)), У(R(νf, C)), У(t), П(Sуд) – f(В) |
|
4. |
Водопоглощение – W |
|||
|
5. |
Усадка – У |
|||
|
С |
6. |
Морозостойкость – F |
П, W, Rсж, t, ρср, νf |
|
|
7. |
Коэффициент радиационной стойкости – kр.ст |
|||
|
8. |
Коэффициент водостойкости – kв.ст |
|||
|
9. |
Коэффициент химической стойкости – kх.ст |
|||
|
10. |
Коэффициент линейного ослабления g-излучения – µ |
Примечания: ρf – плотность наполнителя; ρs – плотность связующего; νf – объемная степень наполнения; C – концентрация активного вещества (например, отвердитель в случае ЭКМ или глицерин в случае ГГЦК); Sуд – удельная поверхность; Рпр – давление прессования, t – время; Т – температура.
Для построения целевой функции качества было выполнено объединение свойств КМ в функциональные группы, внутри которых свойства зависят от одних и тех же факторов, а между группами зависимость минимальна. В табл. 3 показано объединение свойств в группы.
Группа А – плотность и прочность – условно обозначены как функции вида f(Аi). Определяющие характеристики в понятии качества КМ. Зависят как от простейших факторов, так и от сложных комплексных свойств материалов, а также зависят от функций более простых показателей и факторов. В физическом смысле характеризуются как факторы, при увеличении которых качество материала также возрастает.
Группа В – пористость, водопоглощение, усадка – условно обозначены как функции вида f(Вi). Являются эксплуатационными свойствами КМ, обусловленными протеканием в материале наряду со структурообразованием и деструктивных процессов. В физическом смысле характеризуются как факторы, при увеличении которых качество материала снижается.
Группа С – морозостойкость и коэффициенты стойкости КМ в различных агрессивных средах – условно обозначены как функции вида f(Сi). Определяются как отношение показателей до к аналогичным показателям после экспозиции в агрессивных средах. В физическом смысле характеризуются как факторы, при увеличении которых качество материала также возрастает.
Как видно из табл. 3, ряд показателей (выход функции) был определен эмпирически в зависимости от различных факторов. Причем построение эмпирических зависимостей производилось и по результатам реализации математических планов и без математического планирования эксперимента. Это дало набор зависимостей одного и того же свойства, но в зависимости от разного числа факторов. В подобных случаях необходимо выполнить объединение функций по методике [3, 5, 6, 10]. Например, зависимости R(νf, C), R(Рпр), R(t), R(П(ρ(νf, C))), R(T), R(νf, Sуд) необходимо объединить в зависимость вида R(νf, C, Рпр, t, П, T, Sуд) и т.д.
Критерий оптимальности (КО) – признак, на основании которого производится сравнительная оценка возможных решений (альтернатив) и выбор наилучшего. Сущность задачи оптимизации заключается в необходимости выбора наилучшего варианта действий, обеспечивающих достижение вполне определённого, т.е. заданного результата при минимальном расходе ресурсов [7, 8, 9]. Для КМ это выбор наилучшей рецептуры и технологии, обеспечивающих получение КМ со строго заданными структурой и свойствами [1, 2, 7].
Результаты каждого решения характеризуются сочетанием значений нескольких показателей. Чтобы установить, какое из возможных решений лучше, нужно сравнить их по нескольким показателям. В этом случае возникает необходимость в формировании КО, который облегчит сравнительную оценку альтернатив.
Объективная необходимость сравнивать варианты по нескольким несоизмеримым показателям является основной причиной трудностей, которые нужно преодолеть при формировании КО при моделировании и синтезе КМ.
При формировании КО и функционала качества КМ основным методологическим принципом является системный подход к оценке возможных решений. Сущность системного подхода заключается в том, что целесообразность тех или иных изменений объекта определяется с учётом его взаимосвязей, исходя из интересов системы, составной частью которой является рассматриваемый объект [2, 5, 6, 10].
Для оценки качества КМ и управляющих воздействий в виде рецептуры и технологии были построены и исследованы несколько функционалов качества.
1 вид – Ф1. Классический функционал. Вводится функция потерь F(a, x, y), характеризующая величину отклонения ответа модели a(x) от правильного ответа y на произвольном объекте x ∈ X. Функция потерь отыскивается в виде F(a, x, y) = (a(x) – y)2. Функционал качества, характеризующий среднюю ошибку a на произвольной выборке Xm:
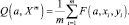 (2)
(2)
В этой связи для оценки качества КМ был использован функционал:
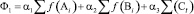
Графическое отображение функционала представлено на рис. 3. Для анализа функций использовалась среда MathCad, v14.
Из рис. 3 видно, что функционал Ф1 помимо экстремума в середине области эксперимента имеет экстремальные значения на одном из краев области, что делает его непригодным для использования в качестве функции качества КМ, т.к. изначально область планирования эксперимента выбиралась таким образом, чтобы экстремумы уравнений регрессий и моделей свойств лежали внутри области планирования.
2 вид – Ф2. Функционал выбирался в виде
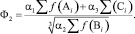
Графическое отображение функционала представлено на рис. 4. Из рис. 4 видно, что функционал Ф2 имеет ярко выраженный экстремум на одном из краев области, что делает его также непригодным для использования в качестве функции качества КМ.
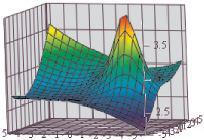
Рис. 3. Функция качества вида Ф1
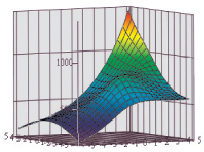
Рис. 4. Функция качества вида Ф2
3 вид – Ф3. Функционал выбирался в виде
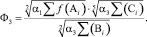
Графическое отображение функционала представлено на рис. 5. Из рис. 5 видно, что функционал Ф3 помимо экстремума в середине области эксперимента имеет экстремальные значения на одном из краев области, что делает его также непригодным для использования в качестве функции качества КМ.
4 вид – Ф4. В основу построения функционала была положена идея о том, что свойства КМ, объединенные в группы А и С, при своем увеличении вызывают увеличение качества всей системы, а свойства, объединенные в группу В – снижение качества системы. Поэтому функционал Ф4 было решено отыскивать а виде сложной дробно-рациональной функции, где в числителе находятся функции свойств групп А и С, а в знаменателе – функции свойств группы В. Функционал принимался в виде
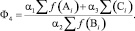
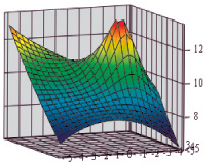
Рис. 5. Функция качества вида Ф3
Графическое отображение функционала представлено на рис. 6. Из рис. 6 видно, что функционал вида Ф4 имеет ярко выраженный экстремум внутри области планирования эксперимента, что доказывает правильность предпосылок о выборе вида функционала качества [3, 5, 7, 10].
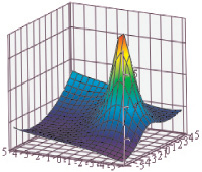
Рис. 6. Функция качества вида Ф4
Дальнейшее исследование функционала Ф4 на экстремум при заданных ограничениях позволило определить область в факторном пространстве, соответствующую наилучшим значениям показателей основных физико-механических и эксплуатационных свойств КМ [1, 2, 3, 6, 10].
Разработанные функционал качества, критерии оптимальности и целевая функция использовались в комплексе программ компьютерно-имитационного моделирования структуры и свойств композиционных материалов при математическом моделировании структуры и свойств композитов, а также при многокритериальном синтезе композитов специального назначения.
Статья публикуется при поддержке гранта № 3018 Базовой части Госзадания вузам на 2016 год.




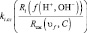 , ki.ст(t), m(ρ(ν
, ki.ст(t), m(ρ(ν