Вопросам оценивания неизвестных параметров регрессионных уравнений посвящена весьма обширная литература [2, 3, 8]. В настоящей статье рассматривается проблема двухкритериального оценивания параметров линейного уравнения регрессии. Стоит отметить, что данная работа методически основана на материале монографии [5].
Главной целью статьи является применение разработанной методики множественного оценивания параметров для решения актуальной задачи моделирования валового регионального продукта Иркутской области.
Краткое описание методики множественного оценивания параметров
Рассмотрим линейное регрессионное уравнение
(*)
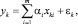
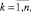где y – эндогенная (объясняемая, зависимая, выходная), а xi – i-ая экзогенная (объясняющая, независимая, входная) переменные; αi – i-й подлежащий оцениванию параметр; ε – ошибки аппроксимации; k – номер наблюдения; n – число наблюдений (длина выборки).
Широкий класс методов оценивания параметров уравнения (*) связан с поиском так называемых Lν-оценок [2] посредством минимизации функций потерь вида
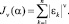
Каждая из этих оценок характеризуется реакцией на так называемые выбросы, то есть наблюдения, не согласующиеся со всей выборкой в целом. При этом чем больше значение ν, тем сильнее Lν - оценка реагирует на выбросы. В регрессионном анализе методы оценивания, слабо реагирующие на выбросы или вообще их игнорирующие, называют робастными.
Методом оценивания параметров уравнения (*), соответствующим ν = 2, является всем хорошо известный и наиболее популярный в регрессионном анализе метод наименьших квадратов (МНК). При ν = 1 это метод наименьших модулей (МНМ), соответствующий городскому расстоянию, а при ν → ∞ – метод антиробастного оценивания (МАО), соответствующий расстоянию Чебышева. В упомянутых выше источниках описаны способы расчета вектора параметров α в соответствии с каждым из трех методов. Использование МНК приводит к аналитическому выражению α = (XTX)–1 XTy, а для отыскания вектора α по МНМ и МАО можно использовать аппарат линейного программирования (ЛП). При этом МНМ- и МАО-оценки являются своего рода антиподами: первая вообще игнорирует выбросы, вторая к ним тяготеет.
Это обстоятельство наталкивает на мысль оценивания параметров уравнения (*) одновременно по двум критериям – J1(α) и J∞(α), то есть по векторному критерию J(α) = (J1(α), J∞(α)). Это позволило бы максимально увеличить информативность процедуры оценивания, извлечь из выборки всю заключающуюся в ней информацию при построении уравнения (*).
Задача минимизации векторного критерия J(α) относится к классу задач многомерного линейного программирования (МЛП). Под решением такой многокритериальной задачи обычно понимают множество Парето P, которое характеризуется тем, что ни одно паретовское решение не может быть улучшено по какому-либо одному критерию без ухудшения значения другого.
Таким образом, решением задачи оценивания параметров регрессии (*) по двум критериям J1(α) и J∞(α) одновременно будет множество оценок. Назовем его L-множеством по аналогии с Lν-оценками [4]. Существует фундаментальная работа американских математиков P.L. Yu и M. Zeleny [9], где изложен так называемый многокритериальный симплекс-метод решения задач МЛП.
Обозначим через P* множество паретовских вершин, через J(P) – образ множества P в критериальном пространстве. В [9] описаны также два способа формирования множества P*. Первый из них имеет итерационный конструктивный характер. Второй же предполагает применение приема последовательного свертывания критериев. Рассмотрим его более подробно.
Сформируем линейную свертку критериев J1 и J∞:
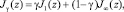γ ∈ (0, 1).
Построим на интервале (0, 1) равномерную ε-сеть:
0 < γ1 < γ2 <...< γl < 1.
Для каждого узла γi,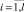 
решим обычную, со скалярной целевой функцией, задачу ЛП:
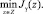
В [9] доказано, что ее решением является паретовская вершина. При достаточно мелкой сети, таким образом, формируется все множество P*.
Безусловно, с такой формой задания модели, в которой параметры определены неявным образом, работать трудно. Поэтому представляется целесообразным иметь какие-то конструктивные приемы, облегчающие эту работу. Рассмотрим некоторые из них.
1. В работе [6] описан способ точечной характеризации множества Парето, позволяющий оперировать не со всем множеством, а с неким его «полномочным представителем», который в какой-то степени отражает в себе свойства всего множества. Таким представителем может быть, например, центр тяжести J0 множества J(P), характеризующий его конфигурацию. Он рассматривается как выпуклая комбинация паретовских вершин многогранника J(P) с равными коэффициентами:
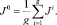
Очевидно, что J0 не будет являться паретовской точкой многогранника J(P). Для определения точки J*, максимально улучшающей J0 по обоим критериям одновременно, необходимо воспользоваться программой отсутствия мажорирования [5].
Решение этой задачи и будет являться искомой точечной характеризацией множества P. Оно может также трактоваться как компромиссное решение задачи оценивания параметров уравнения (*).
2. Рассмотрим способ повышения «осязаемости» в восприятии множества P. Это может быть сделано, в частности, посредством построения множества A
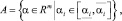
которому гарантированно будут принадлежать вектора α = (α1, ..., αm)T.
A представляет собой параллелепипед в m-мерном пространстве, в который вписана проекция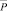 
множества P на Rm.
Легко видеть, что справедливы равенства
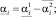
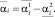
Здесь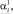 
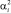и 
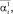
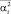– соответственно минимально и максимально возможные значения положительных и отрицательных частей компонент вектора оцениваемых параметров.
Для построения множества A необходимо для каждого параметра αi решить 2(g – 1) следующих задач ЛП:
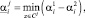
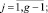
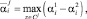
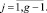
Тогда 
и 
отыщутся по формулам
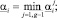
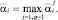
Имея множество A, легко формировать вектора 
для регрессии (*). Но, как правило, A содержит «лишние» параметры, являющиеся компонентами непаретовских векторов. Для того чтобы выявить такие вектора, необходимо всякий раз реализовать программу отсутствия мажорирования.
3. Рассмотрим проблему прогнозирования значений эндогенной переменной y регрессии (*) с множественной оценкой ее параметров.
Пусть заданы значения экзогенных переменных уравнения равны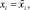 
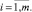Поскольку оценка параметров имеет множественный характер, естественно считать, что соответствующее прогнозное значение переменной y также будет принадлежать множеству – отрезку 
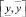. Ниже приведен способ расчета его границ.
Решим 2(q – 1) задач ЛП:
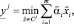
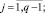
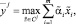
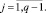
Тогда получим
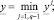
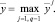
Моделирование валового регионального продукта Иркутской области
Для построения регрессионной модели валового регионального продукта (ВРП) Иркутской области с сайта Федеральной службы государственной статистики были собраны статистические данные за период с 2005 по 2014 г. по следующим переменным:
y – валовой региональный продукт, млрд руб.;
x1 – потребление электроэнергии, млрд кВт•ч;
x2 – численность безработных, тыс. чел.;
x3 – строительство жилых домов, тыс. кв. м;
x4 – оборот розничной торговли, млрд руб.
Значения этих переменных представлены в табл. 1, а их динамика – на рис. 1 и 2.
Таблица 1
Статистические данные
|
Год |
y |
x1 |
x2 |
x3 |
x4 |
|
2005 |
258,1 |
52,5 |
127,5 |
303,0 |
104,3 |
|
2006 |
330,8 |
53,6 |
108,3 |
331,0 |
128,0 |
|
2007 |
402,7 |
53,3 |
104,9 |
575,0 |
151,3 |
|
2008 |
438,9 |
55,1 |
109,9 |
585,0 |
192,1 |
|
2009 |
458,8 |
52,4 |
137,9 |
602,2 |
191,4 |
|
2010 |
546,1 |
54,3 |
127,3 |
629,5 |
197,3 |
|
2011 |
634,6 |
56,7 |
114,9 |
755,2 |
225,8 |
|
2012 |
738,0 |
58,0 |
97,8 |
871,4 |
250,0 |
|
2013 |
805,2 |
56,6 |
104,4 |
829,2 |
266,5 |
|
2014 |
907,4 |
56,3 |
109,7 |
716,9 |
285,9 |
Корреляционная матрица переменных представлена в табл. 2.
По матрице видно, что между зависимой переменной y и каждым из объясняющих факторов x1, x3, x4 имеется сильная положительная корреляция, а между y и x2 – умеренная отрицательная, что вполне укладывается в каноны регрессионного анализа.
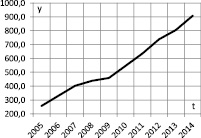
Рис. 1. Динамика ВРП Иркутской области
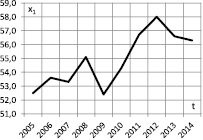
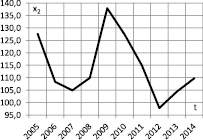
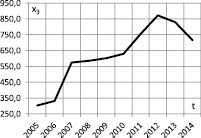
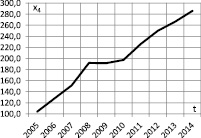
Рис. 2. Динамика влияющих на ВРП показателей
Таблица 2
Корреляционная матрица
|
y |
x1 |
x2 |
x3 |
x4 |
|
|
y |
1 |
0,8248 |
–0,4153 |
0,8647 |
0,9780 |
|
x1 |
1 |
–0,6748 |
0,8277 |
0,8200 |
|
|
x2 |
1 |
–0,4069 |
–0,3610 |
||
|
x3 |
1 |
0,9088 |
|||
|
x4 |
1 |
По корреляционной матрице также видно, что некоторые из объясняющих переменных тесно коррелируют между собой. Следствием этого будет возникновение эффекта мультиколлинеарности при попытке построения, например, линейной модели множественной регрессии. Поэтому для выбора спецификации была реализована технология «конкурса» моделей [1, 7]. В результате была выбрана и оценена по МНК следующая нелинейная по факторам, но линейная по параметрам регрессия:
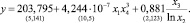
Под коэффициентами этого уравнения записаны значения t-статистик. Для уровня значимости 10 % все коэффициенты значимы. Коэффициент детерминации этой модели R2 = 0,985, критерий Фишера F = 231. Статистика Дарбина – Уотсона DW = 1,96, что говорит об отсутствии автокорреляции в ошибках модели.
Множественное оценивание модели ВРП Иркутской области
Для реализации процедуры множественного оценивания регрессионных моделей в среде программирования Delphi был разработан специализированный программный комплекс. Все представленные ниже результаты получены с его помощью.
Множество Парето J(P*), состоящее из шести вершин, представлено в табл. 3.
Таблица 3
Паретовские вершины
|
J1 |
J∞ |
|
245,6 |
44,23 |
|
235,7 |
44,36 |
|
226,2 |
44,61 |
|
218,4 |
44,9 |
|
197,1 |
46,18 |
|
190,6 |
53,56 |
Множество Парето в критериальном пространстве представлено на рис. 3.
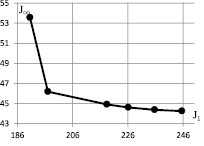
Рис. 3. Множество Парето
1. Точечная характеризация множества P:
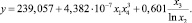
2. Множество A:
α1 ∈ [132,1; 251,1];
α2 ∈ [3,68•10–7; 4,513•10–7];
α3 ∈ [0,4096; 1,665].
3. Для получения прогноза ВРП Иркутской области на 2015 г. были использованы следующие значения объясняющих переменных: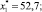 
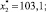
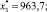
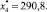Интервальный прогноз имеет вид y ∈ [921,1; 962,6].
Выводы
1. Рассмотрена технология множественного оценивания параметров линейных регрессионных моделей.
2. С помощью технологии организации «конкурса» моделей выбрана структурная спецификация модели ВРП Иркутской области.
3. Проведена процедура множественного оценивания параметров выбранной модели регрессии, с помощью которой получен интервальный прогноз ВРП Иркутской области на 2015 г.
4. Из материала работы следует, что аппарат множественного оценивания параметров является весьма эффективным при моделировании сложных систем и более гибким (мягким) по сравнению с традиционных регрессионным анализом, в рамках которого возможно построение только так называемых точечных (жестких) оценок.