При проектировании стартовых сооружений (СС) нагрузки, воздействующие на СС, как правило, задаются в виде упрощенных аппроксимированных графиков зависимости общей тяги ракеты-носителя (РН) от времени, а различные ее особенности (ударные волны, акустическое давление, пульсации и т.д.) учитываются путем ведения обобщенных коэффициентов перегрузки. При таком представлении пусковой нагрузки не учитывается ряд ее существенных составляющих и, прежде всего, случайные пульсации давления в пограничной зоне турбулентного потока, которые являются основной причиной возникновения вибрационных перегрузок в самом сооружении.
Нагрузка на несущие конструкции СС от газодинамической струи представляет собой довольно сложное сочетание ударных, акустических, температурных полей, а также полей пульсаций давления, распределенных по поверхностям СС, что существенно осложняет расчет сооружения, а порой делает его невозможным.
В связи с этим встает задача определения статистических характеристик полей пульсаций давлений, представляемых в виде равнодействующих сил, приходящихся на ту или иную поверхность СС.
Принимая во внимание сочетание различных факторов и особенностей газодинамических нагрузок, а также сложности решения задач теоретическим путем, возможным решением имеющейся проблемы является путь использования результатов натурных или крупномасштабных модельных испытаний.
Используемый метод определения газодинамических нагрузок, имеющих характер случайных полей пульсаций давлений, состоит в том, что если известны корреляционные и взаимные корреляционные функции между пульсациями давления в различных точках поля, то можно рассчитать силы пульсаций давления, действующих на конструкцию по площади F в целом [4, 5].
При определении равнодействующих сил полей пульсаций давления будем полагать, что поля давлений представляются в виде суммы полей по некоторым отдельным элементарным площадкам ΔFi, равных по своей площади квадратам со стороной радиуса когерентности rk и в пределах которого статистические характеристики давления mx(τ), Dx(τ), Rx(τ) постоянны (рис. 1).
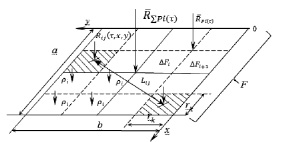
Рис. 1. Формирование поля пульсаций давления и равнодействующей силы пульсаций на площадь F
Как показывают результаты измерений давлений в смежных областях [4, 5], радиус пространственно-временной корреляции r в пределах F затухает весьма быстро (рис. 2) и математически может быть выражен экспоненциальной кривой типа
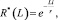(1)
где i – текущая ордината; R*(L) - функция нормированной взаимной корреляции в пределах площади F; r – расстояние, на котором еще наблюдается взаимосвязь пульсаций давлений, т.е. радиус корреляции, при этом значение (r) ограничивается величиной связи, равной 0,1R*(0).
Достаточно точное значение экспоненциальной функции R*(L) может быть неизвестно из-за малого количества точек измерений. В этой связи в расчетах вместо r используется приближенное значение радиуса когерентности rk (рис. 2).
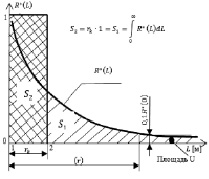
Рис. 2. Определение радиуса когерентности (rk) и максимального радиуса корреляции (r)
Наиболее полной характеристикой рассматриваемой силы равнодействующей полю пульсаций давления по некоторой площади F является выражение корреляционной функции суммы сил [2, 3]:
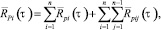(2)
где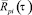 
– автокорреляционная функция пульсации давления, воздействующего на единичную площадку ΔFi; 
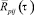– взаимная корреляционная функция, которая характеризует связь пульсаций давления между единичными площадками; n – количество единичных площадок ΔFi.
Будем рассматривать поле нагрузки на общую площадь нагружения F как сумму сил Pi по некоторым единичным площадкам ΔFi (рис. 1) со стороной равной радиусу когерентности rk. Пусть на ΔFi действуют случайные во времени и пространстве центрированные силы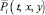 
, которые имеют смысл и размерность давления, если ΔFi – единица площади.
Характеристики пульсаций давления между соседними площадками ΔF и ΔFi+1 будем рассматривать как статистически независимые.
В рамках когерентности и однородности в пределах площади F – взаимная корреляция пульсаций давления переходит в автокорреляцию, т.е.
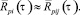(3)
Учитывая, что площадь конструктивного элемента сооружения F состоит из n единичных площадок ΔFi, тогда выражение (3) можно переписать в другом виде:
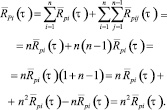(4)
Проведя ряд преобразований и принимая во внимание, что n ~ ΔFi, ΔFi → F, выражение (4) можно переписать в следующем виде:
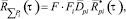(5)
где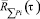 
– корреляционная функция равнодействующей силы суммарного давления на площадь F; ΔFi – некоторая площадка, в пределах которой пульсации давления когерентны, характеризуются дисперсией 
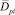и нормированной автокорреляционной функцией (АКФ) 
.
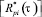Принимая площадку ΔFi равную квадрату со стороной rk, функция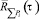 
будет выражаться как
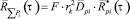[кг2], (6)
принимая τ = 0, получим
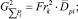
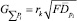[кг]. (7)
Выражение (7) и принятая величина радиуса когерентности rk определяют корреляционную функцию равнодействующей силы, поля пульсаций, приходящейся на площадь F.
Оценивая радиус корреляции пульсаций газодинамического давления r по плите покрытия на реальном объекте, необходимо отметить, что при проведении ЛКИ с изделием «Н-1» № 7 данная задача осложнялась отсутствием должного количества точек измерений. В связи с этим был определен радиус корреляции r, а за ним и радиус когерентности rk лишь в первом приближении для плиты покрытия СС.
В пределах нулевой отметки плиты покрытия сооружения, системой газодинамических и акустических измерений (ГАИ) стартового комплекса в ходе проведения ЛКИ регистрировались пульсации нестационарного давления в четырех точках с параметрами ДН29, ДН31, ДН45, ДН48 (рис. 3). Радиус корреляции r в представленной работе определялся на момент подъема ракеты принятый за расчетный, т.е. на седьмой секунде после контакта подъема (КП). В этот момент на плиту покрытия, конус и газоходы с высоты 92-х метров воздействует газодинамический поток, с относительно выравненными градиентами скоростей, полных давлений и высоких температур, который накрывает всю поверхность плиты сооружения равной 1600 м2.
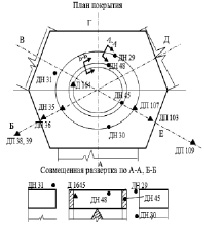
Рис. 3. Схема расстановки датчиков нестационарных давлений на плите покрытия сооружения 358(2)
Длина реализации для вычисления статистических характеристик случайных процессов бралась равной 1 с реального времени. В пределах выбранного отрезка времени случайный процесс рассматривался как стационарный, что в табулированном виде составляло 800 точек квантования на одну реализацию.
При оценке величины r вычисление взаимных временных корреляционных функций пульсаций давления, зарегистрированных в различных точках покрытия (рис. 3, 4), производилось по следующим известным выражениям [1, 3, 5]:
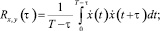(8)
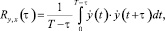
где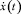 
, 
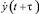– центрированные значения функций x(t), y(t) в разных точках плиты.
Коэффициенты взаимной корреляции Kxy(τ) вычислялись по известным формулам [1].
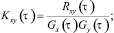
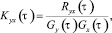(9)
где Gx(τ), Gy(τ) – среднеквадратические значения пульсаций давления в точках измерений.
В качестве центра, относительно которого определялся коэффициент взаимной корреляции Kxy(τ), принята точка ДН 45 (рис. 3). Определение r и rk осуществлялось в следующем порядке:
1. Вычисление последовательно взаимных временных корреляционных функций Rxy(τ) между параметром ДН 45 и остальными параметрами (ДН 48, ДН 29, ДН 31).
2. Коэффициенты взаимной корреляции при τ = 0 откладывались по оси L с учетом расстояния между точками регистрации давлений параметров ДН 45 и ДН 48, ДН 29, ДН 31 (рис. 4).
3. Определение радиуса корреляции r – расстояние вдоль оси L, на котором взаимная корреляция функции R*(L) снижается до значений, составляющих 0,1R*(0).
4. Определение радиуса когерентности rk (рис. 5) при условии
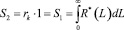(рис. 2).
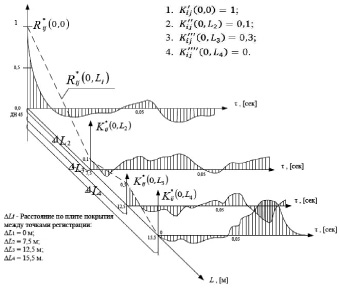
Рис. 4. Определение радиуса корреляции r для плиты покрытия сооружения на основе экспериментальных данных, полученных при ЛКИ № 7
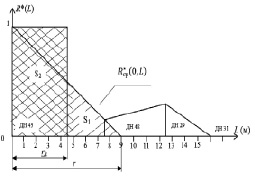
Рис. 5. Определение радиуса когерентности rk и максимального радиуса корреляции r по результатам натурных измерений ЛКИ № 7
Совокупность 
при τ = 0 вдоль оси L определила вид функции R(L), ограничивающей радиус пространственной корреляции – r.
Тенденция изменения, в пространстве функции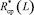 
вычисленная на основе двух ЛКИ № 6, 7, показывает, что связи пространственной корреляции в основном сохраняются от работы к работе. По найденной функции 
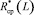и определялся радиус когерентности rk, равный 4,5 м (рис. 5).
Вычисление радиуса когерентности rk для плиты покрытия СС на объекте явилось первым опытом при расчете равнодействующих сил полей пульсаций давлений газодинамических нагрузок. При этом вычисленное rk является несколько завышенным в связи с ограниченным количеством точечных датчиков, что может рассматриваться пока в запас прочности при расчете конструктивных элементов.
Вместе с тем вычисленное rk дает первое представление о степени коррелирования пульсаций давления и определяет направление последующих исследований, нацеленных на вычисление более точных значений rk. Такие исследования возможны при организации работ на крупномасштабных моделях СС путем увеличения числа точечных измерений и уменьшения расстояний между датчиками, регистрирующими пульсации нестационарного давления в газодинамическом потоке.
Конструктивные элементы СС различны по своей конфигурации, площади омывания и ориентации в пространстве относительно направления проходящих газодинамических потоков. В связи с этим, естественно, что rk для них будет своим, что потребует дополнительных измерений и вычислений.
Выводы
Определение нагрузок на тот или иной конструктивный элемент СС на основе использования результатов натурных измерений нестационарных давлений потоков струи стартующей РН является лишь первым приближением и нуждается в дальнейших углубленных исследованиях и уточнениях.
Представленный вариант сбора динамических нагрузок в виде равнодействующих сил случайных полей пульсаций давлений несколько утяжеляет расчет, однако он позволяет оценить частотную составляющую вибрационных нагрузок и возможность возникновения резонансных явлений в ходе запуска. Вычисляемые нагрузки на основе rk являются более близкими к реальной картине воздействия ее на элементы сооружения, что позволит точнее рассчитать несущие конструкции, так и СС в целом, выявив прочностные резервы и более оптимально проектировать СС.