Критерий согласия Пирсона (χ2) применяют для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(x) при большом объеме выборки (n ≥ 100). Критерий применим для любых видов функции F(x), даже при неизвестных значениях их параметров, что обычно имеет место при анализе результатов механических испытаний. В этом заключается его универсальность.
Использование критерия χ2 предусматривает разбиение размаха варьирования выборки на интервалы и определения числа наблюдений (частоты) nj для каждого из e интервалов. Для удобства оценок параметров распределения интервалы выбирают одинаковой длины.
Число интервалов зависит от объема выборки. Обычно принимают: при n = 100 e = 10–15, при n = 200 e = 15–20, при n = 400 e = 25–30, при n = 1000 e = 35–40.
Интервалы, содержащие менее пяти наблюдений, объединяют с соседними. Однако, если число таких интервалов составляет менее 20 % от их общего количества, допускаются интервалы с частотой nj ≥ 2.
Предлагаемая модификация критерия Пирсона [1, с. 80] позволяет проверять гипотезу о предполагаемом распределении генеральной совокупности [5, с. 51], обладающей функцией распределения
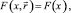
где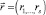 
– известный вектор параметров распределения [2, с. 22].
Разобьем носитель случайной величины на m равновероятных интервалов следующим образом:
1 /m = F(bj) – F(aj) = p; F(a1) = 0;
F(bj) = j/m, j = 1, …, m.
Имеется выборка x1, …, xn из генеральной совокупности, с указанным выше распределением [2, с. 22].
Рассмотрим произвольный интервал (aj, bj) на носителе случайной величины [3, с. 68]. Любое наблюдение из выборки с вероятностью p = 1/m попадает в указанный интервал и с дополнительной вероятностью, равной q = 1 – p, не попадает в него. Для случайной величины vi – числа наблюдений из выборки, попавших в указанный интервал, получаем простую схему Бернулли с вероятностью успеха при одном испытании p и числом испытаний n. Таким образом, получаем m простых схем Бернулли при одинаковых вероятностях успеха p и числа испытаний n [4, с. 392].
В силу локальной теоремы Муавра – Лапласа случайные величины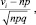 
j = 1, …, m имеют распределение близкое к стандартному нормальному. Предлагаемая модификация критерия Пирсона заключается в выборе критической статистики в следующем виде:
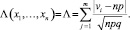
Выбор критической статистики в таком виде обусловлен более устойчивыми ее свойствами. Для применения данного критерия необходимо найти функцию распределения статистики Λ, то есть функцию распределения случайной величины Ym, где
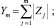
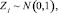j = 1, …, m.
Запишем функцию распределения случайной величины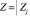 
по определению:
Fz(x) = P(Z < x) = P(–x < Zj < x) = 2Ф(x),
где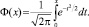 
После дифференцирования левой и правой частей получим выражение для функции плотности Z:
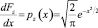
при x > 0 и 0 иначе.
Для дальнейших рассуждений нам потребуется характеристическая функция Z, которая есть по определению:
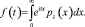
Продифференцируем левую и правую части равенства по t:
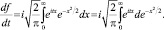
Далее, интегрируя по частям, приходим к следующей задаче Коши:
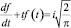
при начальных условиях f(0) = 1.
Как нетрудно проверить, решение этого обыкновенного дифференциального уравнения есть:
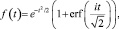
где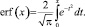 
Интересно отметить, что полученная функция выражается через функцию Фаддеева:
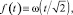
где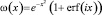 
– есть функция Фаддеева. Тогда характеристическая функция случайной величины
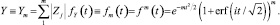
Для нахождения центральных моментов случайной величины Ym вычислим производные от ее характеристической функции в точке t = 0:
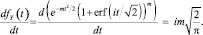
Отсюда получаем
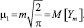
Для нахождения второго центрального момента вычислим вторую производную от характеристической функции в точке t = 0:
,
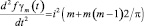и тогда
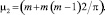
Таким образом, дисперсия
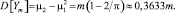
Дисперсия y Xи-квадрат распределения такова
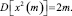
Отношение дисперсий очень красноречиво:
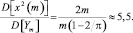
Вернемся теперь к вычислению функции плотности распределения pY(x) = pm(x) через её характеристическую функцию:
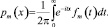
Дифференцируя обе части, получаем следующее:
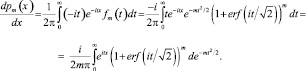
После интегрирования по частям имеем
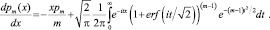(1)
Что приводит к следующей задаче Коши:
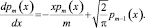(2)
pm(0) = 0.
Положим m = 2, получим уравнение для функции плотности распределения такой случайной величины:
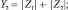
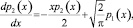
где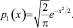 
Решая эту задачу Коши, получаем
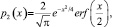x ≥ 0; p2(x) = 0, x < 0.
Решение при m > 2 в явном виде найти сложнее. Поэтому удобнее воспользоваться численными методами. Для этого запишем систему обыкновенных дифференциальных уравнений в векторном виде:
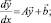
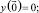
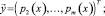
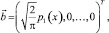
где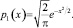 
Здесь A – квадратная матрица размером (m – 1)×(m – 1)
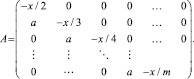
На рис. 1 изображены решения этой системы дифференциальных уравнений, то есть функций плотности распределения случайной величины Ym при m = 2, …, 9. Как известно, для суммы независимых случайных величин есть и другой способ найти функцию плотности распределения через свертку. Для случая m = 2 оказалось возможным непосредственно найти решение
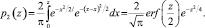
В случае m > 2 численными методами получено решение полностью совпадающее с решениями системы (2). Необходимо отметить, что численное решение системы (2) многократно эффективнее по времени вычисления по сравнению с нахождением функций плотности через свертку.
Рассмотрим использование данной критической статистики для проверки гипотезы о том, что генеральная совокупность имеет функцию распределения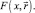 
Практически для всех известных распределений путем моделирования выборки и вычисления критической статистики была построена её (статистики) эмпирическая функция распределения. На том же рис. 2 нанесен график функции распределения, полученный как решение системы (2).
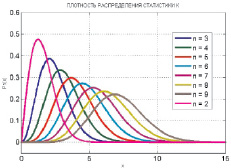
Рис. 1. Плотность распределения статистики Λ
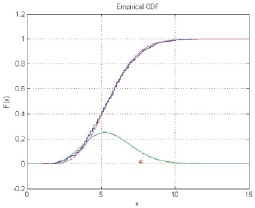
Рис. 2. График функции распределения статистики Λ
Таким образом, для случайной величины Ym,
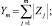
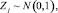j = 1, …, m
получено однопараметрическое семейство распределений со следующими характеристиками:
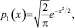x ≥ 0,
p2(x), …, pm(x) – решение системы (2);
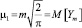– первый центральный момент;
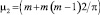– второй центральный момент;
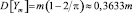– дисперсия;
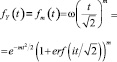– характеристическая функция;
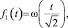
где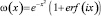 
– функция Фаддеева.