Целью внедрения Интеллектуальных транспортных систем является получение возможности быстро реагировать на изменяющие условия в системе и оптимизировать ее функционирование. Способность контролировать в режиме реального времени распределение корреспонденций по сети и изменения в интенсивности транспортных потоков позволяет прогнозировать возникновение заторов, предотвращать нежелательные последствия резкого роста интенсивности на отдельных участках сети. Значительные усилия ученых в течение последних двадцати лет были направлены на решение задачи прогнозирования матрицы корреспонденций в режиме реального времени, на оценку спроса на перевозки внутри транспортной сети с учетом динамических изменений в интенсивности движения. Данной проблемой занимались Okutani, Stephanedes, Kang, Chang, Tao, Peeta, Ziliaskopoulos, Ashok, Ben-Akiva, Mahmassani и целый ряд других исследователей.
Строить оценку матрицы корреспонденций только на основании исторических данных невозможно, так как поток корреспонденций зависит от большого числа случайных факторов. Даже если прогноз требуется на краткосрочный период. Для обеспечения точности и надежности оценки регрессионную модель изменений в транспортных потоках уточняют с помощью полученных от датчиков показаний. Часто с этой целью применяют фильтрацию Кальмана.
В данной работе предлагается метод оценки динамических изменений в матрице корреспонденций, базирующийся на мезоскопической математической модели распределения транспортных потоков по сети, разработанной автором [5].
Расчет LP-матрицы (матрицы пропорциональных отношений) в динамическом режиме
Матрица корреспонденций (OD-матрица) содержит информацию о числе транспортных средств, проходящих от «источника» к «стоку» в течение времени t:
(1)
где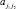 
– число транспортных средств, проходящих от «источника» j1 к «стоку» j2; 
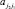– число транспортных средств, проходящих в обратную сторону от j2 к j1.
Традиционно (например, в работе [6]) LP-матрица несет информацию о доле транспортных средств, проходящих по дуге i в течение обследуемого времени t и относящихся к паре «источник – сток» № j. Она должна быть составлена для каждой дуги i транспортной сети. Ее размерность совпадает с размерностью матрицы корреспонденций. В данной работе предполагается хранить в LP-матрице два параметра: количество транспортных средств, соответствующих данной паре и дуге Nij, и долю LPij этих транспортных средств.
Если есть заинтересованность в потоке только между отдельными парами j «источник – сток», то OD- и LP-матрицы формируем только для них.
Предполагается, что для начального этапа off-line составлены OD- и LP-матрицы. Дальнейшая их корректировка на каждом k-м шаге проводится в соответствии с данными об интенсивности движения транспортных потоков по полосам, поступающими с датчиков в режиме on-line. Кроме того, перед началом перераспределения корреспонденций на k-м шаге уже получены матрицы ASTREETS и BINTERSECTION с новыми значениями параметров распределения Эрланга, скорректированными с помощью Фильтра Кальмана [3].
Алгоритм 1 прогнозирования доли транспортных средств, проходящих по каждой дуге и относящихся к конкретной паре «источник – сток», представлен ниже:
1) выбираем пару j «источник – сток»;
2) формируем для пары j множество оптимальных маршрутов (как множество дуг, по которым он проходит) и число транспортных средств, использующих этот маршрут, исходя из принципа равновесия на следующий такт времени;
3) рассчитываем долю транспортных средств, относящихся к паре j на дуге i, она равна отношению интенсивности (Nij)k, соответствующей паре j, к полной интенсивности (Ni)k потока по дуге: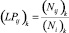 
, если дуга относится к оптимальному маршруту (если дуга не относится к оптимальному маршруту, то доля транспортных средств равна нулю);
4) составляем LP-матрицы для каждой из дуг, учитывая расчеты шага 3, на следующий такт времени;
5) корректируем интенсивность по дугам в матрицах ASTREETS и BINTERSECTION с помощью фильтра Кальмана;
6) переходим к пункту 1.
Второй пункт Алгоритма 1 требует отдельного пояснения. Изменения в интенсивности движения происходят между несколькими парами «источник – сток» (точнее, мы контролируем все пары, входящие в матрицу корреспонденций). Поэтому следует использовать Алгоритм 2 из работы автора [2], в котором на каждом шаге определяются оптимальные маршруты для каждой пары. Расчеты проводятся аналитическим методом с помощью авторской модели TIMeR_Mod. Аналитический метод позволяет повысить скорость расчетов.
Так как временная ось разбита на промежутки малой величины, то можно считать,что оптимальный маршрут, вычисленный в пункте 2 для отдельного требования, соответствующего паре j, остается таковым для всех Δ(Nij)k требований. Поэтому число корреспонденций для пары j на каждом шаге изменяется только за счет изменений по одному маршруту (оптимальному для данного шага).
В пункте 3 следует учитывать следующий факт: если дуга не относится к оптимальному маршруту, то доля транспортных средств равна нулю, пересчитывать ее не надо. Пересчитывать следует только долю тех дуг, для которых наблюдается ненулевое изменение интенсивности Δ(Nij)k для данной пары «источник – сток».
Формирование матрицы корреспонденций по известной матрице пропорциональных изменений в динамическом режиме
Зная матрицу пропорциональных отношений на текущем и предыдущем периодах времени, можно найти процентное изменение числа транспортных средств, относящихся к каждой паре j «источник – сток» для каждой дуги i:
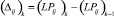– для всех дуг i. (2)
Тогда среднее процентное изменение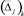 
для пары j на k-м шаге является точечной оценкой истинного изменения числа транспортных средств, относящихся к каждой паре j в текущий момент времени:
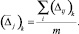(3)
Здесь m – количество дуг, по которым прошел оптимальный маршрут на данном шаге для данной пары j (дуги, процентное изменение для которых в LP-матрице равно нулю, не учитываются).
Тогда прогнозное значение для числа корреспонденций на следующий шаг:
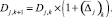(4)
Из элементов Dj,k+1 формируется OD-матрица для следующего шага.
Для формирования LP-матрицы на (k + 1)-й шаг расчитываем:
– изменение интенсивности для пары j на дуге i:
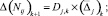
– интенсивность для пары j на дуге i:
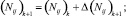
– долю транспортных средств на дуге i, соответствующую паре j:
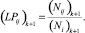
Уточнение LP-матрицы с применением фильтра Кальмана в случае, если известна матрица корреспонденций для всех пар «источник – сток»
При прогнозировании матрицы пропорциональных отношений и матрицы корреспонденций неизбежно возникают ошибки вычислений. Желательно на каждом этапе уточнять одну или другую матрицу, сравнивая вычисленные с помощью модели значения с некоторыми эмпирическими значениями. В данной работе с этой целью используется фильтр Кальмана [3].
Если OD-матрица построена для всех возможных пар j «источник – сток», то справедливо равенство
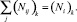(5)
То есть для каждой дуги на каждом шаге сумма интенсивностей, соответствующих интенсивности для пары j на дуге i, равна интенсивности по дуге i. Интенсивность (Ni)k на каждом шаге измеряется с помощью датчиков. Здесь возможны ошибки измерения:
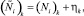(6)
где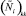 
– измеряемое значение интенсивности на дуге; (Ni)k – истинное значение, ηk – ошибка измерения.
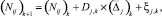(7)
где ξj,k – ошибка модели.
Просуммируем (7) по j с учетом (5):
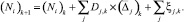(8)
Обозначим
; 
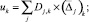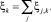
Тогда
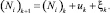(9)
Ошибка модели ξk и ошибка сенсора ηk – случайные величины. И их законы распределения не зависят от времени (от номера итерации k). Средние значения M(ξk) = 0, M(ηk) = 0. Оценку дисперсии случайных величин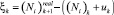 
и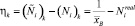 
надо вычислить непосредственно перед началом on-line процесса (см., например, [1]).
Предполагается, что все случайные ошибки независимы друг от друга: какая ошибка будет в момент времени k, совершенно не зависит от ошибки в другой момент времени k′.
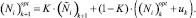(10)
Чтобы найти значение коэффициента Кальмана K, надо минимизировать ошибку:
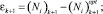
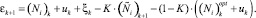
После упрощений получим
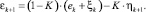(11)
Математическое ожидание квадрата ошибки:
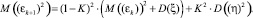(12)
Найдем производную по переменной K, приравняем к нулю. Тогда получим коэффициент Кальмана на шаге (k + 1):
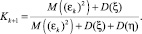(13)
А следовательно,
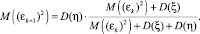
Тогда элементы LP-матрицы уточняем по рекурсивной формуле:
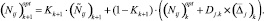(14)
Для начального этапа можно принять
K1 = 0,5;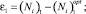 
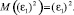
Уточнение OD-матрицы в случае, если требуется контролировать число корреспонденций только между отдельными пунктами «источник – сток»
Если матрица корреспонденций составлена не для всех возможных пар «источник – сток», то равенство (5) не выполняется, а следовательно, контролировать расчетные значения по измерениям интенсивности так, как указано в предыдущем пункте, не представляется возможным.
Если возможно контролировать число убывающих корреспонденций из каждого пункта, указанного в OD-матрице, то возможно корректировать и прогнозные значения матрицы корреспонденций также с помощью фильтра Кальмана.
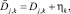(15)
где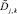 
– измеряемое значение числа корреспонденций на шаге k, соответствующее паре j; Dj,k – истинное значение, ηk – ошибка измерения.
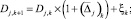(16)
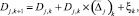
где ξk – ошибка модели.
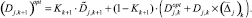(17)
Аналогично предыдущему получим рекурсивные формулы:
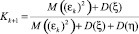– коэффициент Кальмана на шаге (k + 1).
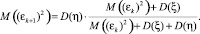
Дисперсии D(ξ) и D(η) должны быть вычислены заранее off-line.
Формула (17) – прогнозное значение элементов матрицы корреспонденций для следующего шага.
Заключение
Оценка и прогнозирование в динамическом режиме матрицы корреспонденций – одна из важнейших задач в транспортной сфере. Метод, предложенный автором в данной работе, учитывает как регрессионную зависимость в изменении распределения интенсивностей потоков транспортных средств, так и случайные факторы, неизбежно влияющие на эти значения. С целью уточнения прогнозируемых данных используется фильтр Кальмана – лучший среди линейных фильтров [4]. Расчеты базируются на идее равновесного распределения потоков по сети и корректируются при каждой итерации. Все это позволяет повысить качество прогнозируемых параметров.
Работа выполнена при поддержке РФФИ и администрации Краснодарского края, проект р-юг-а -16-48-230720.