В последние десятилетия серьёзный импульс развития получило научное направление, связанное с разработкой, исследованием и применением стохастических поисковых алгоритмов оптимизации [5, 3], которые также называют популяционными алгоритмами (или агентными метаэвристиками) [1].
Данные метаэвристики нашли широкое применение в решении оптимизационных задач, общая постановка которых предполагает нахождение допустимого множества решений [7]:
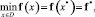 (1)
(1)
где D – является гиперкубом; x* – искомое оптимальное решение; f* – значение целевой функции; f – вектор-функция, представленная следующим образом:
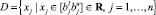
f:D > Rm; f(x) = [f1(x), f2(x), …, fm(x)]T.
На практике множество решений (1) может быть и конечным, но его мощность зачастую настолько велика, что методы перебора в решении становятся неэффективными.
Целью работы является разработка математической модели единообразного представления постановки ряда динамических задач дискретной оптимизации из различных предметных областей со сходной интерпретацией в терминах теории графов для последующего решения на основе алгоритмов агентных метаэвристик.
Материалы и методы исследования
Существует ряд задач из различных предметных областей, для которых существует актуальная востребованность в их решении.
1. Создание траекторий космических перелётов с использованием гравитационного маневра [12, 13].
2. Организация перевозок товаров с ограниченным сроком годности [9].
3. Маршрутизация в распределённых программно-конфигурируемых сетях для динамической миграции виртуальных ресурсов [10].
4. Планирование траекторий индивидуального обучения с учётом эффекта забывания [2].
Несмотря на разнообразие предметных областей, из которых заимствованы перечисленные задачи, последние могут быть единообразно представленными на уровне конкретизированной постановки динамической задачи дискретной оптимизации [7, 8] и сходно интерпретированы в терминах теории графов.
Результаты исследования и их обсуждение
Выполним указанную выше постановку на примере задачи № 1 и далее распространим её описание на остальные. Идеи первой из рассматриваемых задач нашли отражение в фильме «PlanetAnt: Life Inside the Colony – BBC» (Andrew Stephenson, 2012), и впоследствии, с использованием ряда допущений, были заимствованы из работ Максимилиано Василе (Massimiliano Vasile) [17] и Эдмондо Миниски (Edmondo Minisci) [14].
Рассмотрим процесс прокладки маршрута между двумя удалёнными планетами p0 и pn в космическом пространстве. Примем во внимание, что для получения дополнительного разгона (и сокращения издержек по расходу топлива) за счёт известного «эффекта пращи» [2, 8] полёт космического аппарата проходит мимо n – 1 промежуточных (движущихся) планет с целью выполнения около них соответствующих гравитационных маневров. Полёт будет проходить на протяжении T (T ≤ n) временных интервалов (каждый из которых соответствует перелёту между двумя планетами pj и pj+1). Абстрагируясь от деталей, будем считать, что переменными являются усреднённые значения собственной скорости космического аппарата 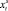 на интервале t и скорости, полученной дополнительно
на интервале t и скорости, полученной дополнительно 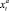 в начале этого периода. Также предположим, что для каждого временного интервала t = 1, 2, …, T известно неотрицательное значение снижения скорости xt (рис. 1).
в начале этого периода. Также предположим, что для каждого временного интервала t = 1, 2, …, T известно неотрицательное значение снижения скорости xt (рис. 1).
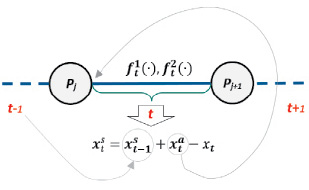
Рис. 1. Характеристики временного интервала t
В соответствии с техническими требованиями, в каждом периоде собственная скорость космического аппарата должна быть не менее 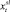 и не более
и не более 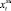 единиц измерения, а интервал возможного изменения дополнительной скорости располагается соответственно между
единиц измерения, а интервал возможного изменения дополнительной скорости располагается соответственно между 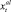 и
и 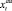 . Логично предположить, что эти параметры неотрицательны (скорость должна быть достаточно велика, чтобы не возымел эффект падения космического аппарата на одну из планет). Ради простоты будем считать, что в начале межпланетного перелёта собственная скорость задана положительной константой из интервала
. Логично предположить, что эти параметры неотрицательны (скорость должна быть достаточно велика, чтобы не возымел эффект падения космического аппарата на одну из планет). Ради простоты будем считать, что в начале межпланетного перелёта собственная скорость задана положительной константой из интервала 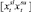 , а первый импульс дополнительной скорости можно получить, только начиная с маневра около планеты p1 (т.е. в начале 2-го периода). Также предположим, что известны некоторые вогнутые функции
, а первый импульс дополнительной скорости можно получить, только начиная с маневра около планеты p1 (т.е. в начале 2-го периода). Также предположим, что известны некоторые вогнутые функции 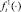 и
и 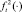 , первая из которых определяет длительность времени межпланетного перелёта в периоде t (или длину траектории от pj до pj+1), а вторая – средний объём расхода топлива в единицу времени (или на единицу расстояния) в зависимости от
, первая из которых определяет длительность времени межпланетного перелёта в периоде t (или длину траектории от pj до pj+1), а вторая – средний объём расхода топлива в единицу времени (или на единицу расстояния) в зависимости от 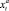 . Важно отметить, что указанные функции имеют соответствующие ограничения
. Важно отметить, что указанные функции имеют соответствующие ограничения 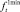 и
и 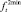 снизу и
снизу и 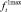 и
и 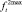 сверху на области допустимых значений.
сверху на области допустимых значений.
Скорость в начале периода t получается, очевидно, из скорости предыдущего периода прибавлением дополнительно полученной скорости в t-м периоде, а также вычитанием издержек снижения скорости в этом периоде.
Предположим, что цель описанного процесса состоит в получении такого межпланетного маршрута G(p), который удовлетворял бы всем ограничениям и минимизировал суммарные затраты при реализации данного перелёта. На рис. 2 показан пример маршрута G(p) = {p0, p3, p4, p7} в двумерном пространстве с тремя интервалами (T = 3) для исходной задачи с семью планетами (n = 7), где пунктиром показаны возможные варианты маршрутов между планетами p0 и p7, сплошной линией – проложенный маршрут между планетами.
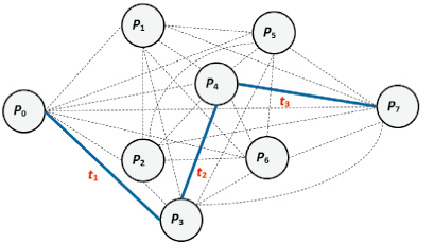
Рис. 2. Пример маршрута G(p) = {p0, p3, p4, p7}
Подобную ситуацию описывает постановка задачи:
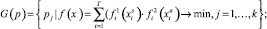
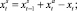
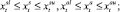
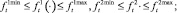
t = 1, 2, …, T; 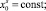
 (2)
(2)
Очевидно, что в данном случае мощность множеств допустимых решений при увеличении числа планет n будет существенно расти, что, как известно, приведёт к неэффективности применения методов перебора для решения сформулированной задачи.
При решении задачи № 2 (организация перевозок товаров с ограниченным сроком годности) описанная выше модель может иметь следующую интерпретацию. Компании-перевозчику необходимо увеличить финансовую выгоду от оказания услуг по перевозке портящихся со временем грузов. В качестве конкретного решения руководство компании предлагает специалистам отдела логистики минимизировать суммарные затраты/издержки для каждого автомобиля компании, задействованного в перевозках.
Предполагается, что процесс работы компании организован следующим образом. Водительский экипаж каждого автомобиля направляется в командировку, состоящую из T временных интервалов, в которой каждый из интервалов t = 1, 2, …, T соответствует одному перегону между городами pj и pj+1 из известного множества городов P = {p0, …, pn}. В городе pj необходимо заправиться и приобрести товар для доставки в город pj+1, где, в свою очередь, необходимо продать этот товар, дозаправить автомобиль, приобрести очередную партию товара для доставки в следующий город и т.д.
Как уже было отмечено, для каждого экипажа необходимо сформировать маршрут на основе принципа «свободного работника», т.е. с минимальными издержками (а следовательно – с максимальной финансовой выгодой). В этой задаче переменными являются сумма денег 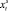 , которая имеется у экипажа для приобретения бензина и закупки товара на интервале t, и объём прибыли
, которая имеется у экипажа для приобретения бензина и закупки товара на интервале t, и объём прибыли 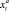 , полученной от перевозки товара на этом же интервале. Будем считать, что товар приобретается из некоторого заранее определённого перечня товаров (обладающих достаточно высокой рентабельностью для выполнения перевозок). Поэтому каждый товар при перевозке позволяет получить некоторый объём прибыли из диапазона от
, полученной от перевозки товара на этом же интервале. Будем считать, что товар приобретается из некоторого заранее определённого перечня товаров (обладающих достаточно высокой рентабельностью для выполнения перевозок). Поэтому каждый товар при перевозке позволяет получить некоторый объём прибыли из диапазона от 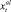 до
до 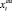 валютных единиц. Также, из соображений безопасности, имеются ограничения на объём возимых денежных средств, сумма которых варьируется в интервале от
валютных единиц. Также, из соображений безопасности, имеются ограничения на объём возимых денежных средств, сумма которых варьируется в интервале от 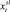 до
до 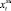 . Помимо этого, для каждого временного интервала t известно неотрицательное значение текущих издержек xt в денежном эквиваленте (средства, выделяемые на питание, проживание экипажа и др.).
. Помимо этого, для каждого временного интервала t известно неотрицательное значение текущих издержек xt в денежном эквиваленте (средства, выделяемые на питание, проживание экипажа и др.).
Очевидно, что в начале командировки сумма затрат на заправку автомобиля и закупку первой партии товара будет определена некоторой положительной константой из интервала 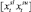 , а первая прибыль будет получена лишь в городе p1 (т.е. в начале 2-го периода). Функции
, а первая прибыль будет получена лишь в городе p1 (т.е. в начале 2-го периода). Функции 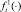 и
и 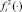 определяют соответственно время, затрачиваемое на доставку товара (например, в зависимости от состояния дорожного покрытия) из города pj в город pj+1 в периоде t, и размер финансовых потерь при перевозке партии товара (из-за его порчи или ухудшения свойств). Как и в задаче № 1, указанные функции имеют соответствующие ограничения
определяют соответственно время, затрачиваемое на доставку товара (например, в зависимости от состояния дорожного покрытия) из города pj в город pj+1 в периоде t, и размер финансовых потерь при перевозке партии товара (из-за его порчи или ухудшения свойств). Как и в задаче № 1, указанные функции имеют соответствующие ограничения 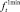 и
и 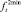 снизу и
снизу и 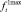 и
и 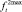 сверху на области допустимых значений.
сверху на области допустимых значений.
Интерпретация и постановка задач № 3 и 4 выполняется аналогичным образом, за исключением иного смыслового трактования переменных и функций в постановке задачи (2) в соответствии с терминологией, принятой в соответствующей предметной области. В данном случае это является предметом готовящихся к публикации отдельных статей и для понимания основной идеи обобщенной постановки задачи существенной роли не играет.
Заключение
Предложенная математическая постановка задачи имеет потенциал вариативной интерпретации не только для ряда рассмотренных задач дискретной оптимизации на темпоральных графах, но и может быть распространена для решения широкого круга задач, не вошедших в перечень проанализированных в данной работе с целью последующего решения на основе алгоритмов агентных метаэвристик [4, 6, 11].



