В условиях кризисного развития экономики страны актуальной остается задача планирования деятельности социально-экономических систем различного уровня, а также экономической оценки эффективности этой деятельности с учетом всех ее составляющих – производственной, инвестиционной, финансовой, управленческой – на основе математического моделирования, автоматизированных программных продуктов и систем поддержки принятия решений (СППР).
Для решения задач планирования деятельности экономических систем целесообразно использовать оптимизационные математические модели в кибернетической постановке [2–6]. Это обусловлено тем, что на основе других моделей трудно выявить потенциал экономической деятельности, и для автоматизированного определения устраивающих лицо, принимающее решения (ЛПР), параметров требуется большое количество численных экспериментов, даже не гарантирующих оптимальности этих параметров. Имеющиеся пакеты программ планово-экономической ориентации в своем подавляющем большинстве не используют оптимизационные модели. При этом имеющиеся численные пакеты, основанные на использовании оптимизационных математических моделей в динамической постановке, как правило, не ориентированы на конечного пользователя и не подходят для применения в условиях оперативного или предварительного анализа задач социально-экономического планирования. В этой связи отметим целесообразность разработки содержательно адекватных, одно- и многокритериальных (оптимизационных), статических, в том числе линейных, моделей.
Опыт моделирования задач планирования и оценки эффективности функционирования экономических систем позволяет указать на ряд особенностей, имеющих междисциплинарный характер. Прежде всего, следует отметить рассогласование концепций моделирования деятельности экономических систем в кругах специалистов-экономистов и математиков-моделировщиков, что, в свою очередь, оказывает влияние и на специалистов, разрабатывающих автоматизированный инструментарий обработки экономической информации. Среди экономистов часто отсутствует понимание того, что, например, для стратегического планирования, требующего в первую очередь применения оптимизационных подходов, моделирование всех доходных и расходных статей не только нецелесообразно, но и, в общем случае, не нужно, и даже вредно. Например, трудно обосновать планирование продажи имущества или других активов проекта, приобретенных на инвестиционные средства по нему, если изначально решается задача определения оптимального количества основных средств и объема производимой продукции именно в этом проекте! По аналогичным соображениям проблематично обосновать необходимость вложения инвестиционного ресурса по проекту в приобретение ценных бумаг других проектов, затраты на рекламу продукции, переобучение работников и пр. Кроме того, часть доходных и затратных статей вообще трудно поддаются какому-либо планированию. Например, из-за отсутствия соответствующих математических моделей практически невозможно прогнозировать возникающие по проекту задолженности.
Другой проблемой взаимопонимания является трактовка мотивации деятельности экономических агентов. С точки зрения тактической, мотивом деятельности производителя в системе является извлечение прибыли, трактуемой в учетно-бухгалтерском смысле как сальдо текущих доходов и расходов, сопутствующих многогранной экономической и финансово-хозяйственной деятельности, включающих десятки доходно-затратных статей. Мотивом стратегического планирования может являться не только извлечение прибыли, имея в виду риски ее отсутствия или недостаточности для финансирования проекта, но и возможность последующей продажи бизнеса или необходимость его сохранения «во что бы то ни стало». В этой связи могут «пригодиться» самые разнообразные возможности достижения этих целей – от продажи имущества проекта, приобретенного на инвестиционный кредит, до использования обеспечивающих текущую платежеспособность серии кредитов «дожития до лучших времен». Для реализации таких возможностей в критерий эффективности стратегической деятельности часто включают поток амортизации как меры имущества или даже «цену» кредита.
При использовании статических моделей функционирования экономических систем адекватное моделирование заемного финансирования деятельности экономических систем требует обязательного разделения этих процессов на инвестиционные (стратегические, долгосрочные) и кредитные (тактические, краткосрочные). При этом стоимость инвестиционного финансирования традиционно учитывается путем дисконтирования потоков прибыли и имущества предприятия через ставку дисконтирования, включающей требования инвестора по возврату средств. Кредитное финансирование текущей деятельности, очевидно, также является платным ресурсом и понижает результативность деятельности, причем как в долгосрочном, так и краткосрочном аспектах. С другой стороны, улучшая текущую платежеспособность экономической системы, кредитное финансирование расширяет возможности ее устойчивого функционирования. Указанные эффекты при моделировании можно учесть, например, включением соответствующих финансовых переменных с положительным знаком в соотношения, описывающие движение денежных средств по проекту, и с отрицательным знаком – в критерий, с учетом оценки стоимости кредита.
Ниже приводится подход к моделированию деятельности экономических систем, учитывающий изложенные выше соображения. Для иллюстрации подхода и его применимости в условиях оперативного принятия решений по планированию экономической деятельности используется статическая многопараметрическая задача линейного программирования (МЗЛП). Искомые переменные разделяются на три группы – производственные, инвестиционные и финансовые. Предполагается, что балансовые, ограничительные и критериальные соотношения, описывающие деятельность экономических систем с содержательно-экономической точки зрения, также учитывают стратегический и тактический характер моделируемых ими условий и потоков. В частности, при описании операционной (производственной) деятельности производственные доходы и расходы разделяются на тактические (выручка от продажи продукции, амортизация, оплата труда, налоги, материальные и другие затраты текущего характера) и стратегические (прибыль, амортизация, инвестиции и другие затраты долгосрочного характера). Отметим, что противоречивое, на первый взгляд, присутствие амортизации в обеих категориях на самом деле объяснимо тем, что экономисты-теоретики трактуют амортизацию как имеющую двойственную сущность экономическую категорию. С одной стороны, как меру текущих затрат на компенсацию износа основных средств, и, с другой, – как меру объема инвестиций (финансовой формы капитала), трансформирующихся в имущество (материальную форму капитала). Финансирование проекта деятельности экономической системы также имеет стратегические (инвестиционные) и тактические (кредитные) формы, краткое описание сути которых приведено выше.
Пусть R – выручка от продажи продукции (товаров и/или услуг) производителя; I – инвестиционные затраты; Cr – кредиты; Dot – дотации; Z – общие производственные затраты; z – оборотные (материальные) затраты; Am – амортизационные отчисления; S0 – остаточная стоимость ОПФ; F – фонд оплаты труда (ФОТ); N1 – налог на добавленную стоимость; N2 – налог на имущество; N3 – налог на прибыль; N4 – страховые взносы предприятия (производителя); N5 – другие налоговые и неналоговые (штрафы, «откаты») затраты производителя. Отметим, что учитываются только налоговые и неналоговые потоки, так или иначе определяемые искомыми объемами производства продукции; αi (i = 1,…,5) – соответствующие законодательно определенные ставки налоговых платежей и отчислений; Т – горизонт планирования проекта развития; p, β – экспертно определяемые параметры, обозначающие соответственно материалоемкость производства и трудоемкость производства, r – годовая ставка дисконтирования, учитывающая инфляцию, уровень требований инвестора и другие возможные, экспертно задаваемые, экономические и политические риски деятельности производителя; r0 – годовая ставка кредита, Т0 – срок кредита; ck, Vk, Tk, Pk, qk – стоимость, производительность, срок полезного использования ОПФ, стоимость единицы продукции и годовой стоимостной спрос на продукцию k-го вида соответственно; δk = PkVk/сk – фондоотдача ОПФ k-го вида (k = 1, …, n).
Функционирование производителя в любой экономической системе происходит в условиях ограничений его деятельности, которые приведены ниже и также разделяются на производственные, инвестиционные и финансовые.
Производственные ограничения: R ≤ min (спрос, фондоотдача ОПФ).
Инвестиционно-финансовые ограничения: DS ≥ 0 – платежеспособность производителя на всем горизонте планирования; I ≤ Imax, где Imax – максимальная сумма инвестиций; Cr ≤ Crmax, где Crmax – максимальная сумма кредита; Dot ≤ Dotmax, где Dotmax – максимальная сумма дотаций.
Чистая приведенная стоимость стратегических потоков производителя обычно представляется в своей динамической форме:
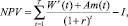
где Wr(t) (t = 1, …, T) – поток прибыли производителя в период [t – 1; t]; Am(t) – поток амортизации в период [t – 1; t].
Несложно показать, что в частном случае, когда для всех t = 1, …, T Wr(t) = W = const и Am(t) = Am = const, значение NPV вычисляется по формуле
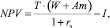
где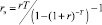 
– эффективная ставка дисконтирования, используемая в случае статического варианта показателя NPV. Критерием производителя является условие: NPV > max. Корректным, на наш взгляд, в этом случае является расчет остаточной стоимости имущества S0 в момент времени Т по формуле
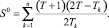
С использованием введенных обозначений, а также описанных ограничений и критериев деятельность производителя может быть описана в форме задачи линейного программирования (ЗЛП) вида
c 1×(2n+2) ·X (2n+2)×1 → max;
A K×(2n+2) ·X (2n+2)×1 ≤ b K×1, (*)
где n – количество видов производимой продукции или видов ОПФ (в соответствии с принципом чистых отраслей); K – количество ограничений, описывающих операционную и инвестиционно-кредитную деятельность производителя; b K×1 – вектор-столбец правых частей ресурсных ограничений; c 1×(2n+2) – вектор-строка коэффициентов целевой функции; A K×(2n+2) – матрица коэффициентов ограничений, нижние индексы указывают размерности матричных величин.
Вектор искомых переменных X (2n+2)×1 состоит из следующих подвекторов и компонент, выраженных в едином, стоимостном измерении: xk – искомый объем инвестиций в k-й вид ОПФ; x n+k (k = 1, …, n) – искомый объем выручки от продажи произведенной и реализованной продукции k-го вида; x2n+1 – искомый объем кредита; x2n+2 – искомый объем дотаций.
Как показано в работах [7–10], указанная структура искомого вектора является достаточной для описания инвестиционной, производственной и финансовой деятельности производителя в экономической системе, как инициатора циркулирующей в ней «экономической энергии».
Выберем за основу алгоритм расчета прибыли производителя, изложенный в работе [6]. Тогда задача планирования деятельности производителя может быть построена в матричной форме, как МЗЛП вида (*), где
b (2n+4)×1 = (0; Imax; 0, …, 0; q1, …, qn; Crmax; Dotmax)T;
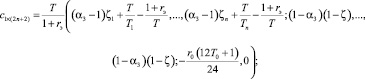
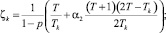
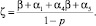
Приведенная выше ЗЛП имеет решение при всех допустимых значениях переменных, в силу принадлежности множеству решений нулевого вектора (X = 0), а также компактности допустимого множества. Наличие нетривиальных решений показано ниже при численном анализе модели. Получив оптимальные (с точки зрения максимизации NPV) значения вектора X, можно рассчитать соответствующие ему показатели финансово-хозяйственной деятельности предприятия. Для финансового анализа построенной в форме МЗЛП модели используется оптимизационный программный продукт «Карма», подробно описанный в [1] и представляющий собой СППР, так как содержит модули занесения и контроля входной информации, графического, многопараметрического и многокритериального анализа МЗЛП, а также элементов финансово-хозяйственной деятельности.
На рисунке приведены зависимости NPV реального бизнес-проекта от горизонта его планирования, а также оптимальные значения кредитов и дотаций, при нижеследующей входной информации: n = 1; c1 = 80000; T1 = 20; V1 = 5110; q1 = 100000; p = 0,2; β = 0,2; α1 = 0,18; α2 = 0,02; α3 = 0,2; α4 = 0,3; α5 = 0; Imax = 80000; Crmax = 6000; Dotmax = 10000; T = 4; r = 0,3. Заметим, что изображенные на рисунке распределения NPV, приводящие к возникновению потребности в дотации или кредите в оптимальном режиме (графики при P1 = 5;10), возникают, как правило, при таких условиях его реализации, когда характеристики эффективности проекта находятся в диапазонах своих рисковых, критических значений. В этом случае внешний (платный или относительно бесплатный, дотационный) финансовый ресурс как раз и играет свою роль рыночного стабилизатора проекта в смысле увеличения запасов его финансовой устойчивости, несмотря на потери результативности. Следует отметить, что текущие рыночные цены единицы продукции, наблюдавшиеся в реальном проекте, находились в диапазоне P1 = 35–40 ден. ед., что свидетельствовало об эффективности и прибыльности проекта и его возможностях финансирования без привлечения кредитного ресурса. Использование пакета [1] позволяет наглядно отражать информацию о жизненном цикле проекта, сроках его окупаемости, максимальных значениях NPV, а также пороговых, с точки зрения задачи оптимального заемного финансирования, значениях варьируемых параметров.
Проведенные расчеты позволили получить результаты, обосновывающие оптимальные объемы, ставки и сроки кредитования в условиях наличия потребности в кредите или дотации. При этом ЛПР имеет возможность выбора оптимальных для него значений указанных параметров, с точки зрения возможных потерь NPV, в широком диапазоне их изменения.
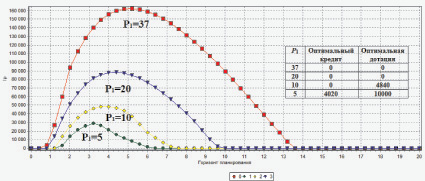
Зависимость NPV(Т) при варьировании параметра P1 = 5; 10; 20; 37
Таким образом, описанный в работе инструментарий позволяет определять оптимальные значения параметров финансирования текущей деятельности производственной подсистемы некоторой социально-экономической системы для повышения ее финансовой устойчивости и срока безубыточности жизненного цикла.